Contents

Gradually Varied Flow

Steady non-uniform flow in a prismatic channel with gradual changes in its water surface elevation

For example,

  • backwater produced by a dam or weir across a river

  • drawdown produced at a sudden drop in a channel

In gradually varied flow (GVF)

  • velocity varies along the channel

  • bed slope, water surface slope, and energy slope will all differ from each other

Note

Bottom slope \(S_0\) changes from one reach to the next, but is constant within a particular reach. (i.e. no slope change within a reach). In practice the slope changes are used to help delineate reaches.

Two basic assumptions in GVF analysis

  • Pressure distribution at any section is assumed to be hydrostatic

  • Gradual changes in the surface curvature give rise to negligible normal accelerations

  • Resistance to flow at any depth is assumed to be given by the corresponding uniform flow equation, such as the Manning’s formula with the condition that the slope term to be used in the equation is intended to be the energy slope (\(S_f\)) and not the bed slope

\[ S_f = (\frac{Q}{\frac{\alpha}{n}AR^{2/3}})^2\]

where \(\alpha=1\) (SI units) and \(\alpha=1.485\) (US customary units).

Differential Equation of the Water Surface

Recall from our specific energy discussion the various components of the Modified Bernoulli’s equation for an open channel

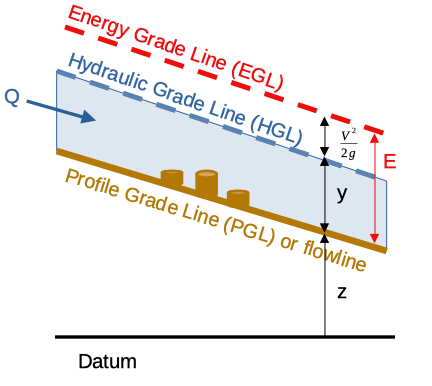
\[ y_1 + \frac{\alpha V_1^2}{2g} + z_1 = y_2 + \frac{\alpha V_2^2}{2g} + z_2 + h_{L;1\rightarrow2}\]

The total head at any cross section is (taking \(\alpha\) as unity for some visual simplicity)

\[ H_i = y_i + \frac{V_i^2}{2g} + z_i \]

The slope of the EGL is something like

\[ -\frac{dH_i}{dx} = \frac{dy_i}{dx} + \frac{d \frac{V_i^2}{2g}}{dx} + \frac{dz_i}{dx} \]

Note

The minus sign because energy is decreasing in the +x direction

Substitute in some geometry to get into a discharge form (which is often more useful!)

\[ -\frac{dH_i}{dx} = \frac{dy_i}{dx} + \frac{d \frac{Q_i^2}{2gA_i^2}}{dx} + \frac{dz_i}{dx} \]

Now make some observations: the slope of the EGL is the friction slope, and the last term is the channel slope at that location.

\[ -S_f = \frac{dy_i}{dx} + \frac{d \frac{Q_i^2}{2gA_i^2}}{dx} - S_0 \]

Calculus the … on the middle term with \(Q\)

\[ -S_f = \frac{dy_i}{dx} -2 \frac{Q_i^2}{2gA_i^3}\frac{dA_i}{dy}\frac{dy_i}{dx} - S_0 \]

Recall \(\frac{dA_i}{dy}\) is just the topwidth at the section

\[ -S_f = \frac{dy_i}{dx} -2 \frac{Q_i^2}{2gA_i^3}T_i\frac{dy_i}{dx} - S_0 \]

A wee bit of algebra

\[ -S_f + S_0 = \frac{dy_i}{dx}(1 -\frac{Q_i^2}{gA_i^3}T_i) \]

Observe the term in parenthesis is \(1-Fr_i^2\)

So the expression becomes (dropping the \(_i\) subscript

\[ \frac{dy}{dx} = \frac{(S_0 - S_f)}{(1 -Fr^2)} \]

And we have an ordinary differential equation of the water surface. A plot of a particular solution, \(y(x)\) is called the water surface profile.

Classification of Water Surface Profiles

Process of identification of possible flow profiles as a prelude to quantitative computations

  • As \(y \rightarrow y_n\), \(\frac{dy}{dx} \rightarrow 0\) , i.e. the water surface approaches the normal depth line asymptotically.

  • As \(y \rightarrow y_c\), \(\frac{dy}{dx} \rightarrow \infty\), i.e. the water surface meets the critical depth line vertically.

High curvatures at critical depth zones violate the assumption of gradually-varied nature of the flow,
thus GVF computations have to begin or end a short distance away from the critical-depth location.

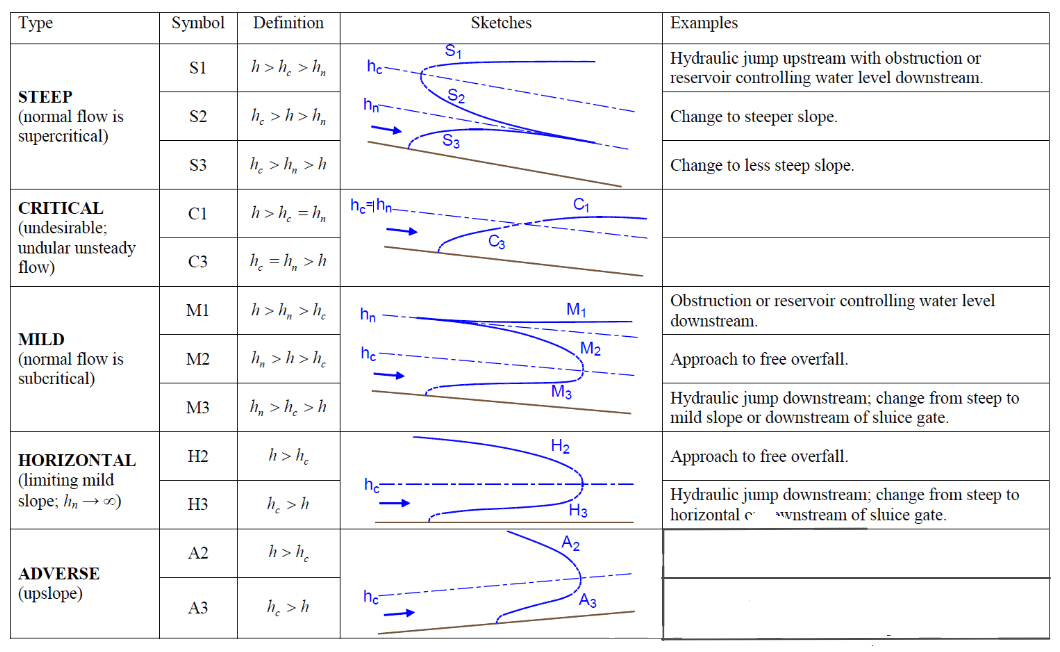
From our textbook

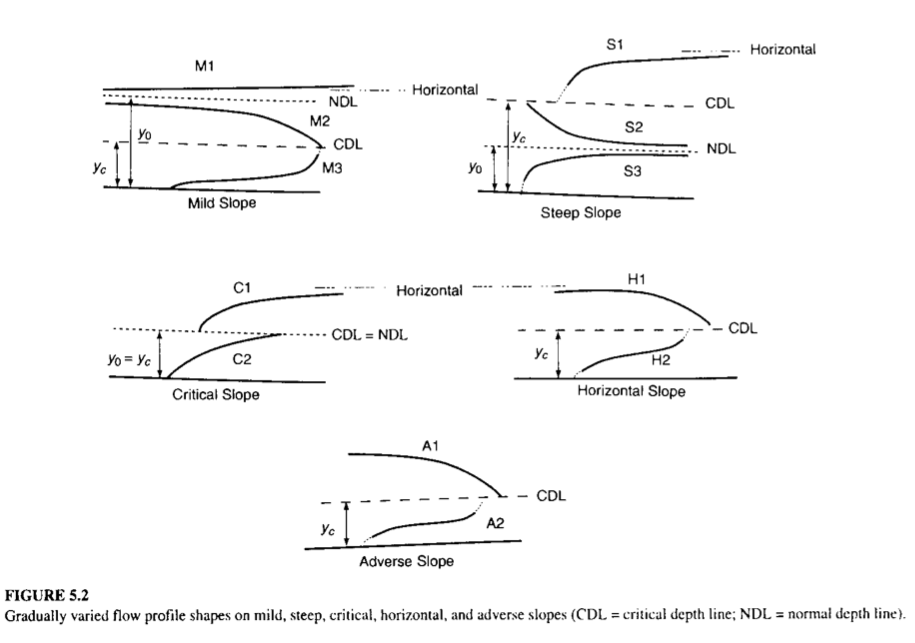
Note

The designations “mild” and “steep” are determined from the relative position of \(y_n\) and \(y_c\) values, not necessarily the slope of the physical bottom of the channel although in most cases the parallel is indeed true.

Control Sections

Section in which a fixed (unique?) relationship exists between the discharge and depth of flow.

  • Weirs, spillways sluice gates are some typical examples of structures which give rise to control sections.

  • Critical depth is also a control point.

  • It is effective in a flow profile which changes from subcritical to supercritical flow. Such

Control sections provide a key to the identification of proper profile shapes.

  • Subcritical flows have controls in the downstream end

  • Supercritical flows have controls in the upstream end

The direction of computation of subcritical profiles is upstream, and for supercritical, it is downstream.

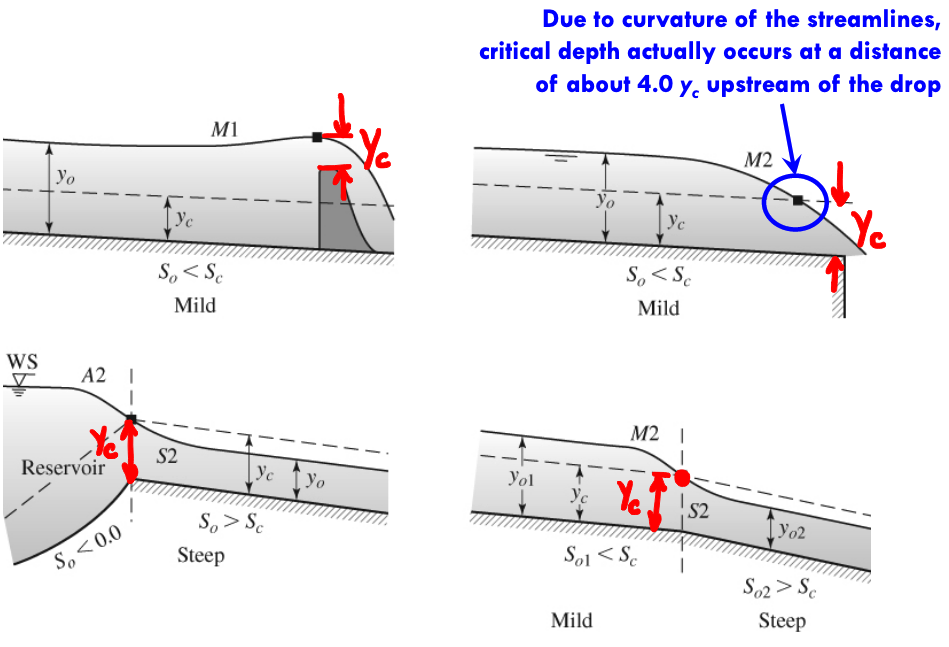
From our textbook, some profiles with control points:

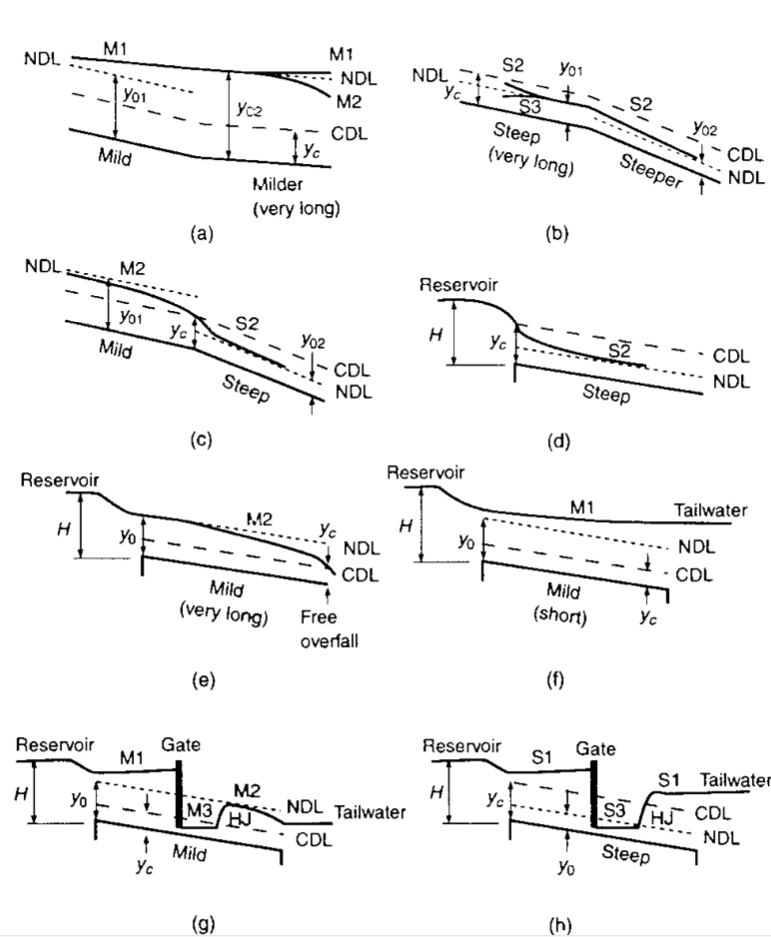
Practice possible profiles

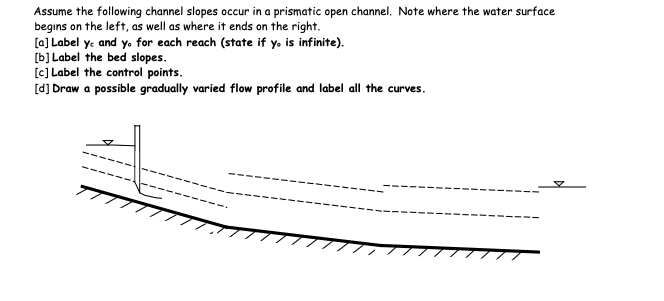
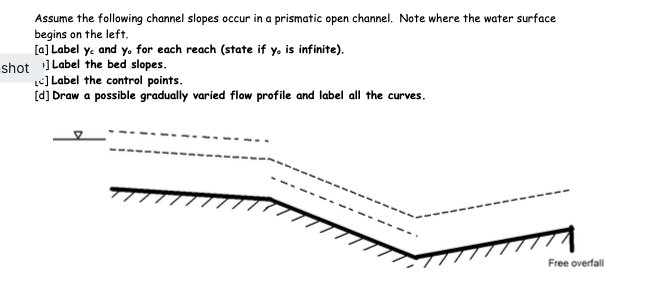
Practice possible profiles

Lake Discharge Type Problems

Similar in spirit to the classic flow between two reservoirs in pipe flow, the connecting conduit can be an open channel.

Whether the channel behaves as hydraulically steep or mild affects how solutions are found.

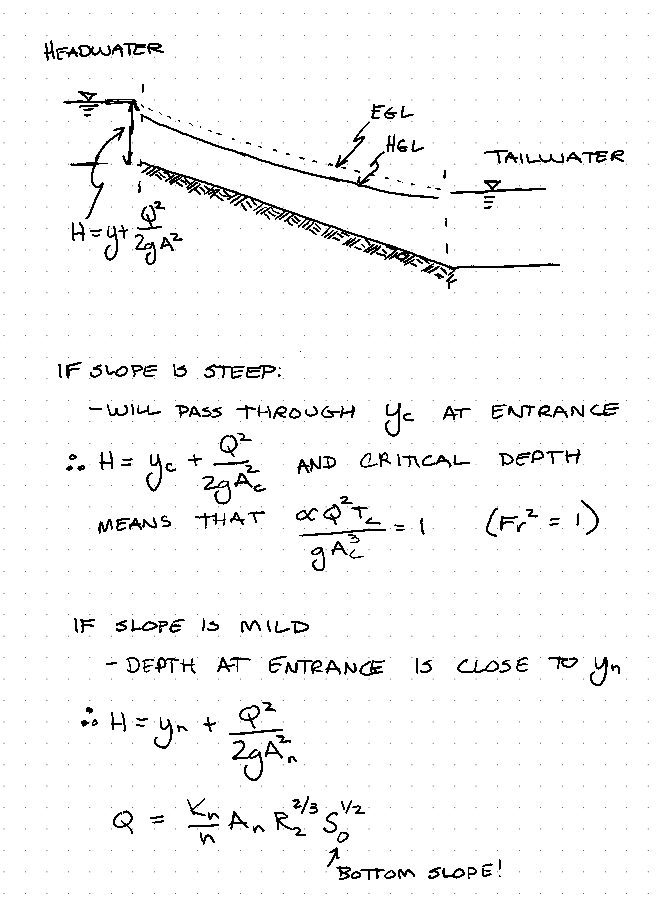
Consider the example in the textbook

A long wreckedangular channel connects two reservoirs with slope of 5%. The channel is 10 meters wide, with Manning’s n of 0.030. The upstream reservoir surface is 3.50 meters above the channel bottom (headwater pool depth relative to channel invert) and the tailwater pool elevation is 2.50 meters above the outlet invert. Estimate the steady discharge in the channel.

Solution

# prototype functions

def Arect(depth,width):
    Arect=depth*width
    return(Arect)

def Prect(depth,width):
    Prect=depth*2 + width
    return(Prect)

def MCE(depth,width,slope,konstant,mann,gee):
    qqq = (konstant/mann)*Arect(depth,width)*((Arect(depth,width)/Prect(depth,width))**(2/3))*slope**(1/2)
    MCE = depth + (qqq**2)/(2*gee*(Arect(depth,width)**2))
    return(MCE)
import math

W = 10.0 #given
S0 = 0.005 #given
n = 0.030 #given
HW = 3.50 #given
TW = 2.50 #given
g = 9.81 #Napolean's fault the dumb little squirt declared the meter a bit too long.
tolerance = 0.0001
# Assume steep

print("(1) Assume channel is hydraulically steep")

ycrit = (2./3.)*HW
Q = math.sqrt( g*(Arect(ycrit,W)**3)/W )

print("   y_c :",round(ycrit,3)," Q :",round(Q,3))

# Check limiting slope
K = 1.0

slopeL = (n**2)*(Q**2)/((K**2)*(Arect(ycrit,W)**2)*((Arect(ycrit,W)/Prect(ycrit,W))**(4/3)))

print("(2) Compute Limiting Slope : ",round(slopeL,3))

if S0 < slopeL:
    print("(3) Test Limiting Slope \n    Bottom slope smaller than limit slope, so channel is hydraulically mild")
    print("(4) Iteratively find flow depth for mild slope from MCE function, report result(s)")
    for i in range(10000):
        dtest = i*(HW)/10000+0.00001 #small offset to prevent zero depths
        nrg = MCE(dtest,W,S0,K,n,g)
        if abs(nrg-HW) <= tolerance:
            print("    Flow depth y: ",round(dtest,3)," Energy E: ",round(nrg,3)," HW Energy HW:",round(HW,3))
            print("    Discharge Q:",round((K/n)*Arect(dtest,W)*((Arect(dtest,W)/Prect(dtest,W))**(2/3))*S0**(1/2),3)," cubic meters per second")
else:
    print("\n    Bottom slope greater than limit slope, so channel is hydraulically steep, use solution(s) above")

(1) Assume channel is hydraulically steep
   y_c : 2.333  Q : 111.635
(2) Compute Limiting Slope :  0.011
(3) Test Limiting Slope 
    Bottom slope smaller than limit slope, so channel is hydraulically mild
(4) Iteratively find flow depth for mild slope from MCE function, report result(s)
    Flow depth y:  2.869  Energy E:  3.5  HW Energy HW: 3.5
    Discharge Q: 100.929  cubic meters per second

References