Volumetric and Mass Flow Rate¶
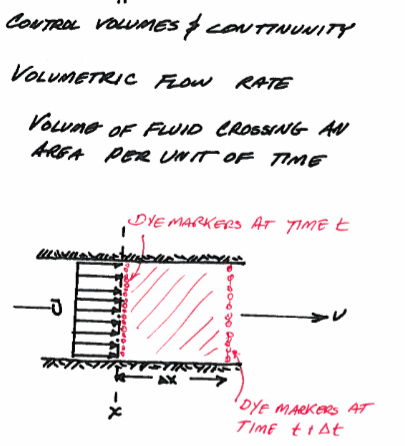
Consider a conduit with cross section area, \(A\).
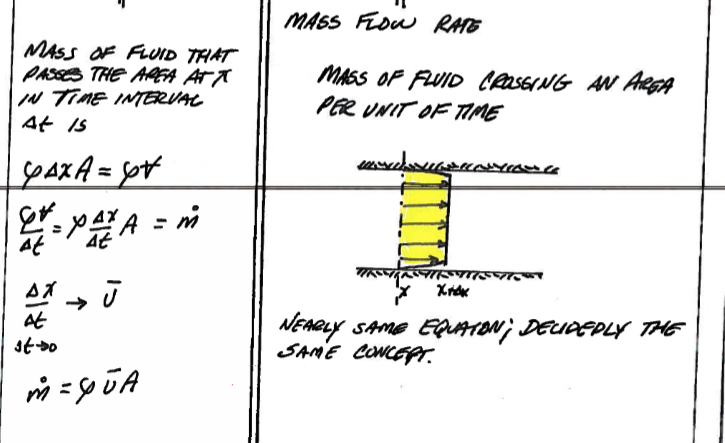
The volume of fluid that passes area \(A\) at location \(x\) in some time interval \(\Delta t\) is given by \( A \Delta x = V\)
The flow rate is \(Q = \frac{V}{\Delta t} = \frac{\Delta x}{\Delta t}A\), the “velocity term” \(u = \frac{\Delta x}{\Delta t}\) is the “mean section velocity”.
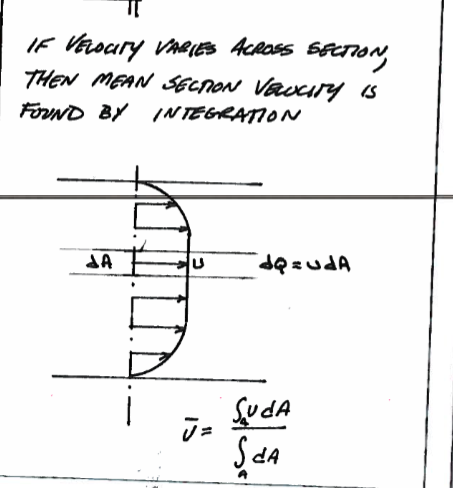
If the velocity varies over the cross section one can obtain the mean section velocity by integration; and in fact this is how streamflow is determined.
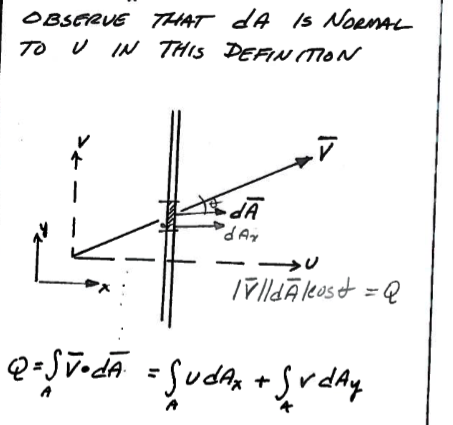
If the orientation is not orthogonal the integrals are the result of the inner product of the velocity vector \(\bar V\) and the area vector \(\bar {dA}\)
The mass flow rate is the product of the volumetric rate and the fluid density
As with volume, the mass flows also are obtained by inner products as:
Example: Flow in a Rectangular Conduit¶
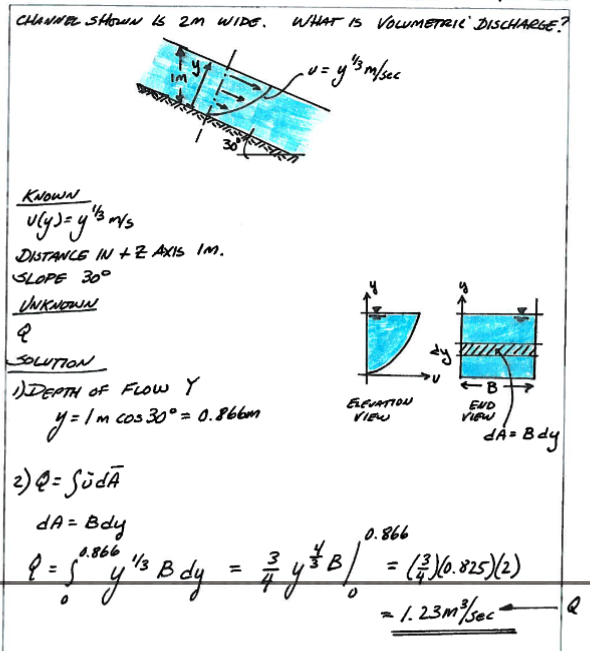
Example: Flow in a Triangular Conduit¶
Control Volumes (pp. 178)¶
A control volume (CV) is the equivalent of a free-body diagram in other fields of engineering mechanics (statics, dynamics).
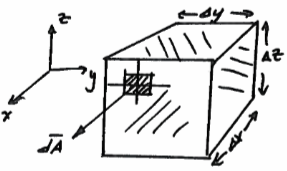
A control volume is some defined area in space, as depicted by the cube below.
Note
The control volume is the basis of Reynolds’ transport theorem that is employed to allow analysis from a Eulerian reference frame rather than tracking individual particles. The goal is to describe fundamental laws of mechanics in integral form
The bounding surface is called the control surface (CS)
The outward pointing area vectors for each face are shown above; these play an important role in application of CV analysis.
The principle is to express various conservation principles in integral form including:
Conservation of mass (continunity)
¶
\(\frac{dm}{dt}|_{sys} = 0\)
Conservation of linear momentum
¶
\(m\frac{d\bar V}{dt}|_{sys} = \sum \bar F\)
Conservation of angular momentum
¶
\(m\frac{d\bar \omega}{dt}|_{sys} = \sum (\bar r \times \bar F)\)
Conservation of energy
¶
\(\frac{E}{dt}|_{sys} = \frac{dQ}{dt} - \frac{dW}{dt}\)
where \(Q\) is heat flow into the system and \(W\) is work done by the system.
Entropy principle
¶
\(\frac{S}{dt}|_{sys} >= \frac{1}{T}\frac{dQ}{dt}\)
where \(Q\) is heat flow into the system, S is entropy, and T is the absolute temperature of the system.
The first four conservation principles are the most useful in fluid mechanics problems; the last principle is applied in various forms in mechanical and chemical thermodynamics problems - its relevant in Civil and Environmental Engineering, but covered in later classes.