Contents

Problem Solving and Documentation (pp 11-13)

Three major work components for the course are:

  1. Exercises (called “Exercise Sets”)

  2. Quizzes

  3. Exams

Warning

All the above instruments should be engaged with a mindset of engaging in the practice of problem solving as a process (regardless of how difficult the actual problem may be). Most of the problems are Cheggable; however the Chegg solutions are pretty minimal and often incorrect (Input values change, and the tutors dont fucking read the problems). Use Chegg if you wish with this limitation in mind - beware in other classes Chegg is considered cheating; You are warned!

The exercises and exams (and to a lesser extent the quizzes) purpose is threefold:

  1. Practice a systematic method to solve and document closed engineering problems;

  2. Develop a type of “muscle memory” in applying the process;

  3. Become accustomed to documenting effort so that others can replicate your work.

The fundamental protocol is

  1. State the problem

  2. Sketch the situation

  3. List known quantities

  4. List unknown quantities

  5. Identify and list governing principles, assumptions, and equations

  6. Analyse the problem - solve for the unknowns

  7. Discuss the results; validate when possible, examine effect of changing an assumption.

There is also an issue of format or the visual structure of a solution. The use of Jupyter Notebooks as your computation tool is expected - as part of a documentation process and the WCOE’s integration of computational thinking throughout the curriculum. Most problems you will work a large part by hand then transfer the computational burden the the Jupyter Notebook.

Throughtout the class do your best to adhere to this format, in some cases it will seem dumb, but thats the nature of training - embrace the “dumbness” now, so you dont have to be dumb later on.

Note

Some exercise sets have an “Easy-Button” which link to YouTube videos of the solutions worked out somewhat, by all means use the EZ button to help you with your exercises. Be aware the videos are kind of rambling, and are longish (nearly an hour in a few cases) - but you can fast forward as you see fit to efficiently work your exercises.

An illustrative example follows (It is a homework problem of sorts, so examine the format somewhat)

Suggested Exercise Solution Format (Paper-Based)

The format will differ if you prepare a Notebook, or work the problem entirely by-hand. Here is an example worked out on paper which will be repeated in a Notebook.

../../_images/example-1-1.png

Fig. 1 Example of fluid mechanics homework problem solution format (page 1 of 4)

Fig. 1 is a screen capture of the problem with the first four solution protocol items listed. The author used headings (underlined) in the figure to keep track of the protocol items. Also observe the simplistic sketch - a device to organize knowns and unknowns.

../../_images/example-1-2.png

Fig. 2 Example of fluid mechanics homework problem solution format (page 2 of 4)

Fig. 2 is a screen capture of the solution process. Here the author uses various definitions of volumes, mass, and the ideal gas law to try to find the sought after quantity. Part way into the solution an additional quantity was needed - simply add that known or governing principle where needed and make a note as done in the example.

../../_images/example-1-3.png

Fig. 3 Example of fluid mechanics homework problem solution format (page 3 of 4)

Fig. 3 is a screen capture of the solution. Here the author uses the computed volumes, mass, and the ideal gas law to solve for the desired quantity. Then a unit conversion is applied because the problem was stated in mixed (SI and Imperial) units. Finally the results are discussed from a problem solving perspective; so years later anyone reading will understand the thinking process applied for the problem.

../../_images/example-1-4.png

Fig. 4 Example of fluid mechanics homework problem solution format (page 4 of 4)

Fig. 4 is a screen capture of a Periodic Chart of Elements. Here it is included as a citation for the source of the molar masses of the gasses in the problem. The URL is circled on the chart, again establishing a persistent citation to the data source.

Suggested Exercise Solution Format (Jupyter Notebook)

Note

Here we will repeat the example. Because this “lesson” is actually a Jupyter Notebook, I am embedding some code directly into the “lesson” - you will not need to mix markdown code blocks with actual code in your notebooks

Name
R Number
Date

Problem Statement
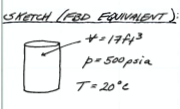
Find the total weight of a 17 \(ft^3\) tank of nitrogen at 500 \(psia\). The vessel itself weighs 50 \(lbf\). The gas is stored at a temperature of 20 \(^o~C\)
Sketch
This is the hardest part, draw the sketch, then save as a png file and embed using

![](filename.png)

like so:

../../_images/FBD-tank.png

Known Quantities
Here we will be mixing code and text

# This is a code cell
vol_tank = 17 # tank volume in cubic feet
p_gas = 500 # gas pressure in psi
temp = 20 # gas temperature in celsius
wt_tank = 50 # tank weight in pounds

Unknown Quantities>br>

Our unknowns are

wt_gas
wt_total = wt_tank+wt_gas

Governing Principles

  1. \(pV=\frac{m}{M}RT\) Ideal gas law

  2. \(wt_{total} = wt_{tank}+wt_{gas}\) Duh!

  3. \(R = 0.0821 \frac{L \cdot atm}{K \cdot mol}\) Definition of universal gas constant

  4. \(T_{K}=T_{C}+273\) Definition of Kelvin temperature scale

  5. \(1 atm = 14.7 psi\) Unit conversion

  6. \(M_{N_2} = 28.014 \frac{g}{mol}\) Molar weight of nitrogen gas

Solution
Now simply produce a sequential script to solve for total weight

mwN2=28.014 # MW nitrogen
R = 0.0821 # universal gas constant
grabity = 9.8 # acceleration of gravity
vol_tank_l=vol_tank*((1/3.28)**3)*1000 # tank volume in liters
temp_k=temp+273 # temp in kelvin
p_atm=p_gas*(1/14.7) # gas pressure in atmospheres
mass_gas = (p_atm*vol_tank_l*mwN2)/(R*temp_k) # gas mass in grams
wt_gas = mass_gas*grabity/1000 # weight of gas in newtons
wt_total = wt_tank + wt_gas*(2.2)/grabity # total weight in pounds
print('Total weight = ', round(wt_total,1),' pounds')

Total weight =  92.0  pounds

Discussion
Probably would want a little more description in the calculation sequence, notice units are reported with the answer. If we want to get fancy, could embed a database for common gasses, and some interactive inputs - but that’s overkill. In practice, you will find a hybrid of paper-based and notebook-based problem solving is most useful.