Stability (pp. 88-90)¶
A floating body is STABLE if, when it is displaced, it returns to equilibrium. A floating body is UNSTABLE if, when it is displaced, it continues to move to a new equilibrium.
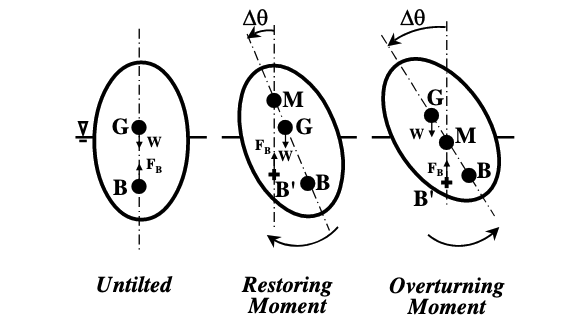
Fig. 81 Object floating in some liquid; tilted a bit - if the bouyancy-weight couple tends to return to initial position, then stable - otherwise will continue to overturn.¶
Consider a floating body tilted by an angle \(\Delta \Theta\), as shown in Fig. 81. For the untilted body the point G is the centre of gravity of the body where the body weight, W, acts. The point B is the center of buoyancy (the centroid of the displaced volume of fluid) where the upward buoyancy force, FB, acts.
When the body is tilted the centre of buoyancy moves to a new position, B’, because the shape of the displaced volume changes. A new point, M, may be defined, called the METACENTRE. This is the point where a vertical line drawn upwards from the new centre of buoyancy, B’, of the tilted body intersects the line of symmetry of the body. The buoyancy force, FB, now acts through B’.
From the center diagram in the figure we observe that W and FB generate a RESTORING MOMENT (Righting Moment) that rotates the body back to its untilted position. From the right hand diagram in the figure we can see that W and FB generate an OVERTURNING MOMENT that rotates the body even further in the tilted direction (the body gets too turnt!).
Thus; if the metacenter, M, lies above the center of gravity, G, then the body is stable. In other words the METACENTRIC HEIGHT, MG, is positive (\(MG = z_M - z_G > 0\)). If the metacentre, M, lies below the centre of gravity, G, then the body is unstable. In other words the metacentric height, MG, is negative (MG < 0).
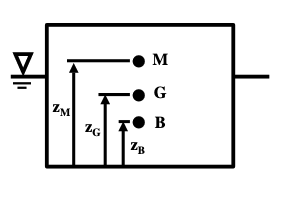
Fig. 82 Reference sketch for center of bouyancy and metacenter distances.¶
The metacentric height, MG, is given by
\(MG = MB - GB = \frac{I}{V_s} - GB\)
where where I is the 2nd moment of area of the plan section of the body where it cuts the waterline (this is the solid plane surface you’d see if you cut horizontally through a solid body at the water surface lifted the top part up and looked at the bottom of it!), VS is the submerged volume (i.e. volume of fluid displaced) and GB is the distance between the centre of gravity and the centre of buoyancy (\(= z_G – z_B\)). Fig. 82 is a reference sketch for the various distances.
Strategy for solving buoyancy/stability problems¶
The usual problem solving protocol works fine, but the additional governing principles/solution algorithm include:
From geometry of body and density of fluid and body equate; Weight of displaced fluid = Total weight of body. This gives the depth of immersion of the body or the weight of the body, whichever is unknown.
To assess stability, first find the location of the centre of gravity G of the body.
Then, find the location of the centre of buoyancy B (centroid of displaced volume). For a regularly shaped body this will be at half the height of the immersed portion of the body.
Calculate the distance GB.
Calculate MB, using MB = I / VS. Note \(I = \pi \frac{D^4}{64}\) for a circular section body and \(\frac{bd^3}{12}\) for a rectangular section body (D is diameter, b and d are the sides of the rectangle).
Calculate metacentric height, \(MG (= z_M – z_G)\), from MG = MB – GB. If MG > 0 then body is stable. If MG < 0 then body is unstable.
Example¶
A solid cylindrical pine (SG=0.5) spar buoy has a cylindrical lead (SG=11.3) weight attached as shown in Fig. 83.
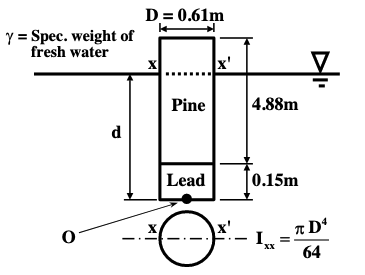
Fig. 83 Schematic of a spar buoy.¶
Determine:
The equilibrium position (i.e. depth of immersion) of the buoy in seawater (SG=1.03).
The metacentric height and show that the buoy is stable.
# sketch here
list known quantities¶
9800 N/m^3 specific weight of water
11.3 SG lead
0.5 SG wood
1.03 SG sea water
0.61 m diameter of spar
0.15 m length of lead portion
4.88 m length of wood portion
list unknown quantities¶
Metacentric height, MG and stability classification
governing principles¶
Definition of metacenter
Definition of center of bouyancy
Definition of canter of gravity
Analytical geometry (as appropriate)
solution (step-by-step)¶
The solution is encoded below using principles of Computational Thinking (in this case sequential programming structure)
import math
rhog = 9800 #N/m^3 sp. weight of water
sgpb = 11.3 #SG lead
sgpine = 0.5 #SG wood
sgseaw = 1.03 #SG sea water
D = 0.61 #m diameter of spar
hpb = 0.15 #m length of lead portion
hpine = 4.88 #m length of wood portion
A = (math.pi*D**2)/4
weight_lead = hpb*A*sgpb*rhog
weight_pine = hpine*A*sgpine*rhog
weight_spar = weight_lead+weight_pine
hseaw=weight_spar/(A*sgseaw*rhog)
CG_bouy = (weight_lead*(hpb/2) + weight_pine*(hpine/2+hpb))/(weight_spar)
CB_bouy = hseaw/2
GB = CG_bouy - CB_bouy # distance from CG to CB
I = A*(D**2)*4/64 #2nd moment of area at waterline (for a circle this case)
VS = hseaw*A #Volume submerged portion
MB = I/VS # Distance from metacenter to center of bouyancy
MG=MB-GB # Compute metacentric height
if MG >= 0.0:
print("Metacentric height ",round(MG,3)," meters ")
print("Bouy is self-righting STABLE")
else:
print("Metacentric height ",round(MG,3)," meters ")
print("Bouy is self-tipping UNSTABLE")
Metacentric height 0.454 meters
Bouy is self-righting STABLE
discussion¶
How tall can the pine portion be before the bouy becomes unstable?
We could do analysis like:
If the buoy is stable when MG > 0 and unstable when MG < 0, we can say that the limit between being stable or unstable is when MG = 0. In this case MB = GB.
One could redo the problem, setting the length of the pine section as L (instead of 4.88m), and equating MB = GB, you can solve for L (by trial and error) to give the maximum length before instability sets in.
Or we can simply use the script we just built and adjust the length of the pine portion until the classification is unstable like:
import math
rhog = 9800 #N/m^3 sp. weight of water
sgpb = 11.3 #SG lead
sgpine = 0.5 #SG wood
sgseaw = 1.03 #SG sea water
D = 0.61 #m diameter of spar
hpb = 0.15 #m length of lead portion
#############################################
hpine = 7.207 #m length of wood portion ##
#############################################
A = (math.pi*D**2)/4
weight_lead = hpb*A*sgpb*rhog
weight_pine = hpine*A*sgpine*rhog
weight_spar = weight_lead+weight_pine
hseaw=weight_spar/(A*sgseaw*rhog)
CG_bouy = (weight_lead*(hpb/2) + weight_pine*(hpine/2+hpb))/(weight_spar)
CB_bouy = hseaw/2
GB = CG_bouy - CB_bouy # distance from CG to CB
I = A*(D**2)*4/64 #2nd moment of area at waterline (for a circle this case)
VS = hseaw*A #Volume submerged portion
MB = I/VS # Distance from metacenter to center of bouyancy
MG=MB-GB # Compute metacentric height
if MG >= 0.0:
print("Metacentric height ",round(MG,3)," meters ")
print("Bouy is self-righting STABLE")
else:
print("Metacentric height ",round(MG,3)," meters ")
print("Bouy is self-tipping UNSTABLE")
Metacentric height -0.0 meters
Bouy is self-tipping UNSTABLE
So for this problem a 7.21+ meter long pine spar is unstable, anything shorter will work as desired.
