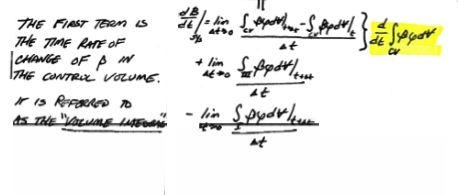Contents

CV Relationships for Mass Conservation (Continunity) (pp. 179)

To use CV analysis the system equations are converted to volume variation relations. Recall that extensive properties are defined throughout an entire mass of a fluid (a system) whereas intensive properties are an amount of property per unit mass.

RTT applied to conservation of mass

Starting with mass itself, the extensive property is mass \(m\)

The mass per unit mass is unity; \(\frac{m}{m}=1\)

The mass per unit volume is density; \(\frac{m}{V}=\rho\)

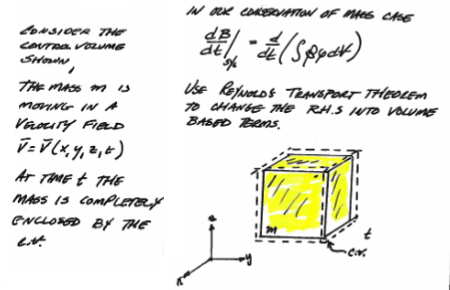
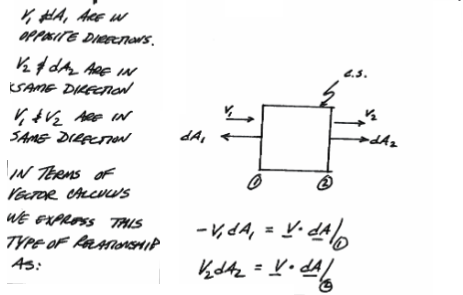
In the case of mass we have

../../_images/rtt-mass.png

Now consider a system (gold cube in the figure at time \(t=t_0\)

../../_images/rtt-mass-t0.png

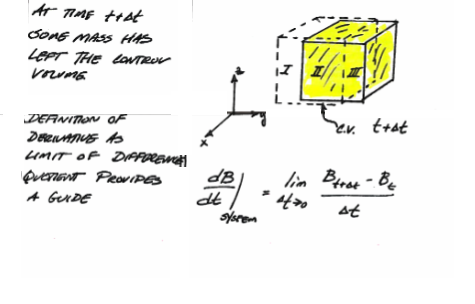
A short time (\(t+\Delta t\)) later the system has moved, some parts have left the CV.

../../_images/rtt-mass-tdt.png

Examination of the three zones and the system total mass gives:

../../_images/rtt-mass-tdt-1.png

Inserting these into the system to volume expression:

../../_images/rtt-mass-tdt-2.png

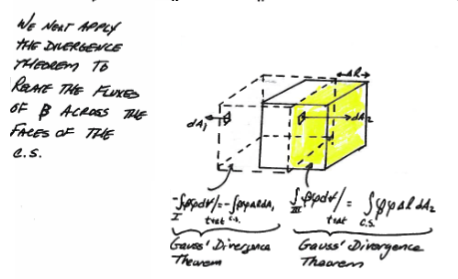
Now using the divergence theroem to cope with the terms in Parts I and III of space in the drawing

../../_images/divergence.png

The application of Gauss’ divergence theorem produces the “flux integrals”.

../../_images/divergence-2.png

Now examine the relationship between velocity and area in the flux integrals

../../_images/vdotDA.png

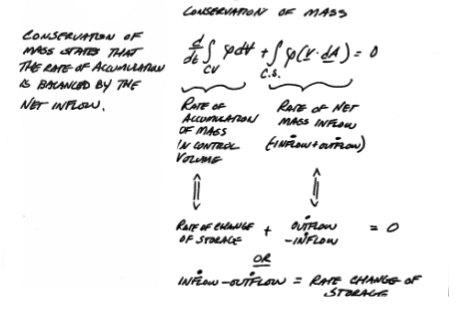
Collect the terms together into the Reynolds Transport Expression for Mass

../../_images/RTT-MassBalance.png

To summarize:

../../_images/rtt-summary.png

Example 1: Application of Continunity to a Holy Grail

Actually our just a vessel with a hole in the bottom; a grail, with a hole in the bottom is the holey grail!

../../_images/example-1.png 
# problem statement - above Yay!

# sketch

# known
V_in = 7 # m/s
A_in = 0.0025 # m^2
Q_out = 0.003 #m^3/s
# rho = 1000 # kg/m3
# grabity = 9.8 # m/s/s

# change in storage
dSdt = V_in*A_in - Q_out
print('storage accumulation is .... wait for it ...',dSdt)

storage accumulation is .... wait for it ... 0.014500000000000002