Applications of Linear Momentum (pp. 284-297)¶
The linear momentum principle is used to find forces on objects that are changing the flow field, or forces from the flow field on those objects
Objects introducing forces are things like pumps
Forces of flow on objects are things like
Flow effects on bridge piers
Flow effects on wind turbine support columns
Flow effects on projectiles
Static forces were studied earlier such as
Retaining walls
Dams
Application of Momentum to a Jet Pump¶
A water jet pump has jet area of 0.01 sq.m. and jet speed of 30 m/s. The jet is within a secondary stream of water having speed 3 m/sec. The total duct area is 0.075 sq.m. The water is completely mixed in the pump and exits at uniform velocity; find the speed at the pump exit and the pressure rise in the pump.
The problem statement is explicitly repeated in Fig. 105

Fig. 105 Caption¶
Apply our problem solving protocol as in Fig. 106

Fig. 106 Caption¶
Note on the CV diagram to draw:
the +/- directions
the CV/CS
the \(\bar dA \) vectors, and
the \(\bar V \) vector(s)
Then apply continunity and momentum to find the unknown values as in Fig. 107
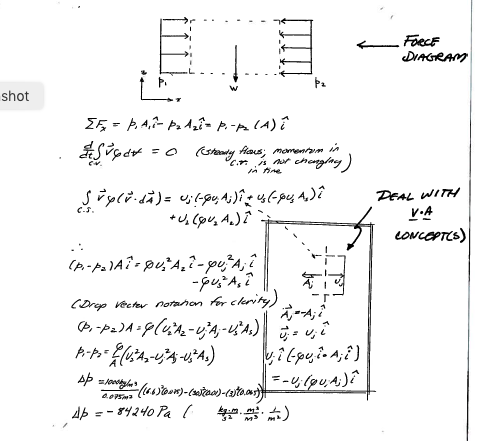
Fig. 107 Caption¶
# computational thinning
u_jet = 30.0
u_approach = 3.0
a_jet = 0.01
a_approach = 0.065
a_total = 0.075
rho = 1000.0
# continunity
u_exit = (u_jet*a_jet+u_approach*a_approach)/a_total
# momentum
delta_p = -(rho/a_total)*(a_total*u_exit**2 - a_jet*u_jet**2 - a_approach*u_approach**2)
# results
print("Pump exit velocity ",round(u_exit,3)," meters per second")
print("Added pressure ",round(delta_p,3)," Pascals")
Pump exit velocity 6.6 meters per second
Added pressure 84240.0 Pascals
Application of Momentum to Find Forces in a Pipe Fitting¶
Consider a pipe fitting as depicted in Fig. 108
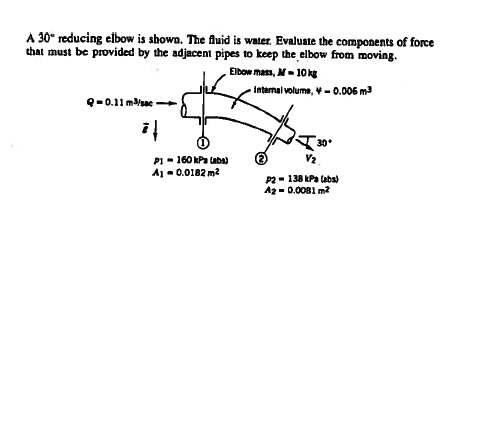
Fig. 108 Caption¶
Apply our problem solving protocol as in Fig. 109
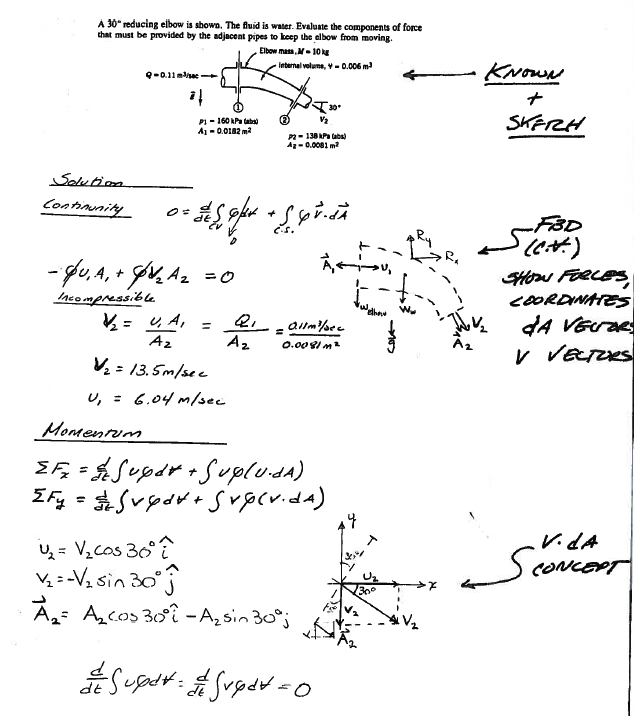
Fig. 109 Problem Solving Protocol: Sketch, CV Definition, Governing Principles, Knowns and Unknowns¶
Apply our analysis tools as in Fig. 110

Fig. 110 Application of linear momentum in the two coordinate directions¶
Application of Momentum to Find Force on a Sluice Gate¶
Consider finding the force on a sluice gate (underflow from a powerhouse) as depicted in Fig. 111
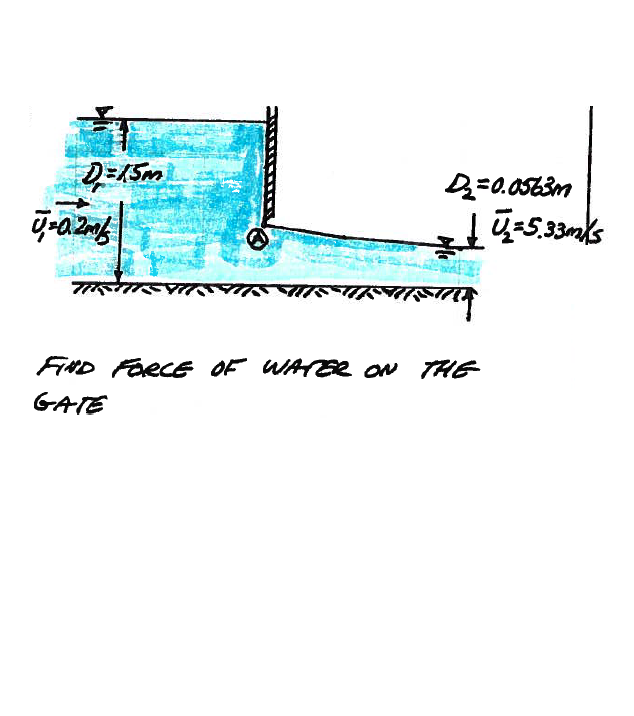
Fig. 111 Schematic elevation view of a sluice gate¶
Upon first inspection one would be tempted to treat the gate as a submerged plate and use hydrostatic calculations, except at point A the pressure is atmospheric, same as at the free surface just upstream of the gate, so the required conditions for hydrostatic analysis do not apply in this case.
So instead of trying to find pressure on the gate, find force of gate on the water, then by eth equal-opposite action-reaction (Newtons’s 2nd law) we can find force of water on the gate .
A first step is to draw a control volume as depicted in Fig. 112
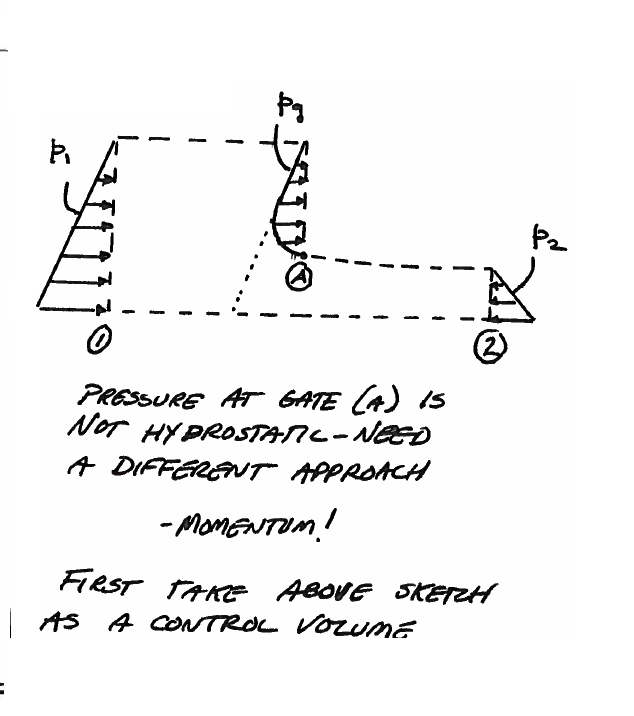
Fig. 112 CV/CS for sluice gate¶
Using the figure as a guide draw:
the +/- directions
the CV/CS
the forces
the \(\bar dA \) vectors, and
the \(\bar V \) vector(s)
The resulting sketch is shown in Fig. 113
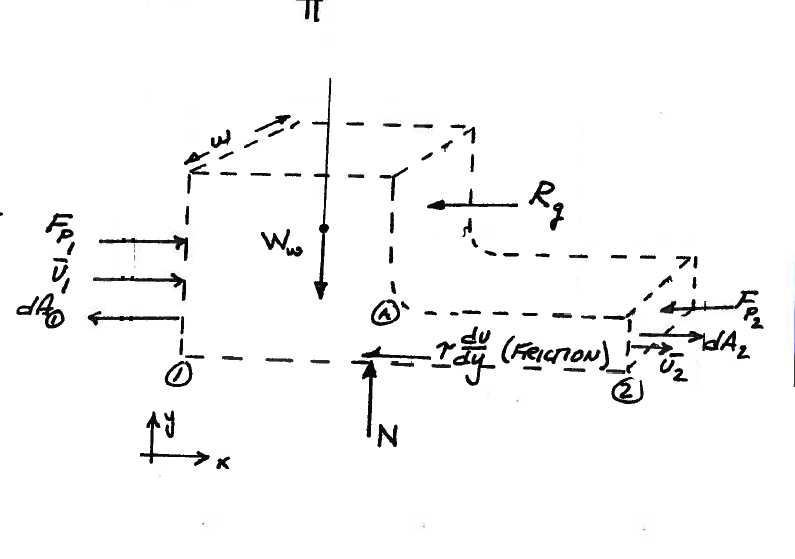
Fig. 113 CV/CS for sluice gate¶
Some assumptions are in order; in particular the distance upstream and downstream are relatively small (a few hundred feet) and the frictional contribution is small by virtue of having only a short distance to act, so we neglect the frictional component. Using the velocity and area directions to resolve the inner products in the flux integrals produces the diagram in Fig. 114

Fig. 114 CV/CS for sluice gate¶
The two pressure forces are some distance from the gate and are hydrostatic and computed using that equation.
\(p = \gamma \bar h\) as depicted in Fig. 115
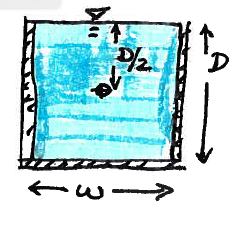
Fig. 115 Pressure force diagram¶
Fig. 116 is a skecth showing the collection of forces on the CV
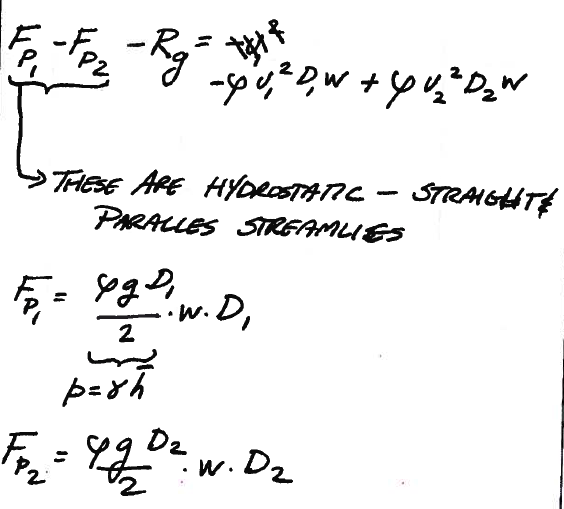
Fig. 116 Forces on CV¶
Fig. 117 completes the analysis; then we can generalize for any sluice gate (in rectangular channles) using ENGR-1330 principles as shown in the script below.

Fig. 117 Forces on CV¶
Sluce Gate Calculations¶
d1 = 1.5 # depth upstream
d2 = 0.0563 # depth downstream
u1 = 0.2 # upstream velocity
u2 = 5.33 # downstream velocity
rho = 1000.0 # density
g = 9.8 # gravitational acceleration
w = 1.0 # channel width
Rg = (0.5*rho*g)*(d1**2 - d2**2)+rho*(d1*u1**2 - d2*u2**2)
print('Upstream Depth',d1,' m')
print('Upstream Speed',u1,'m/s')
print('Downstream Depth',d2,' m')
print('Downstream Speed',u2,'m/s')
print('Force/width',round(Rg,2),'N/m')
Upstream Depth 1.5 m
Upstream Speed 0.2 m/s
Downstream Depth 0.0563 m
Downstream Speed 5.33 m/s
Force/width 9470.05 N/m
Application of Momentum to Estimate Shallow Wave Speed in a Channel¶
Consider a shallow wave in a rectangular channel as in Fig. 118

Fig. 118 Problem Statement¶
First we draw a control volume as in Fig. 119
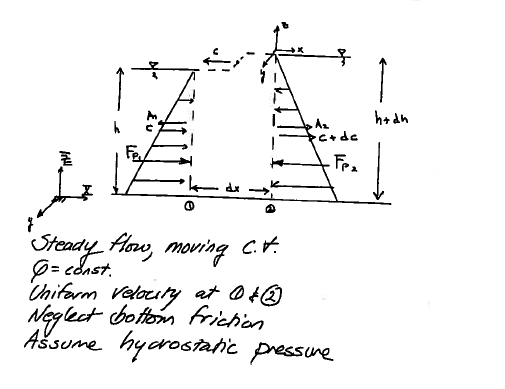
Fig. 119 Sketch¶
Then apply continunity to find the apparent velocities as in Fig. 120
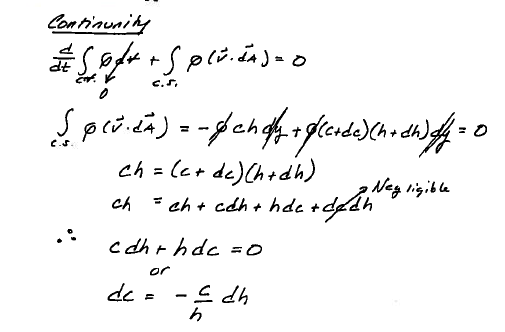
Fig. 120 Continunity application¶
Then apply momentum as in Fig. 121
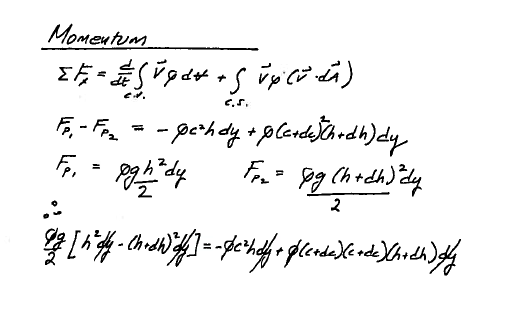
Fig. 121 Momentum application¶
Complete the analysis to find the shallow wave speed as in Fig. 122

Fig. 122 Analysis results¶
