Volumetric and Mass Flow Rate (pp. 168-174)¶
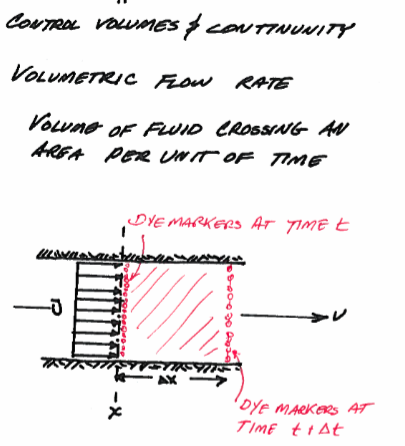
Consider a conduit with cross section area, \(A\).
The volume of fluid that passes area \(A\) at location \(x\) in some time interval \(\Delta t\) is given by \( A \Delta x = V\)
The flow rate is \(Q = \frac{V}{\Delta t} = \frac{\Delta x}{\Delta t}A\), the “velocity term” \(u = \frac{\Delta x}{\Delta t}\) is the “mean section velocity”.
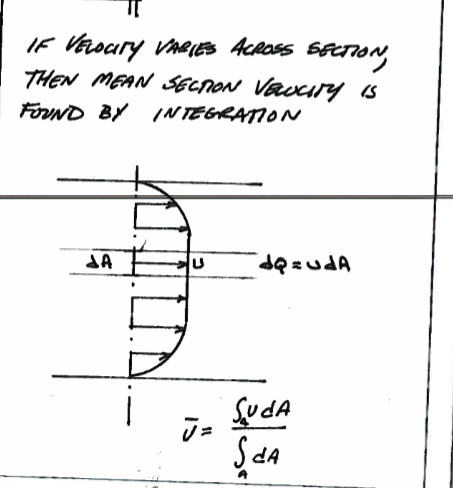
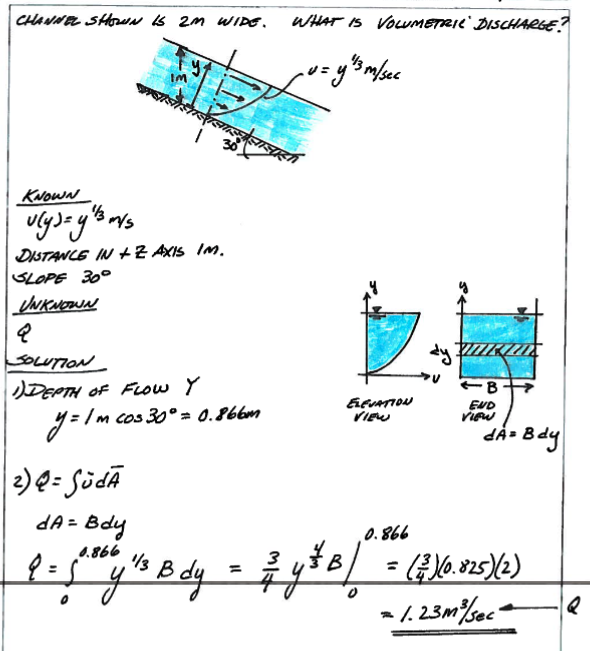
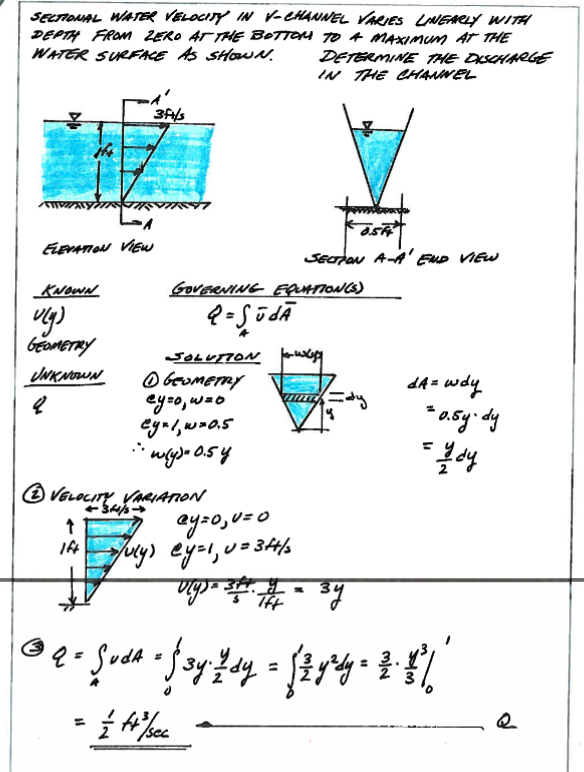
If the velocity varies over the cross section one can obtain the mean section velocity by integration; and in fact this is how streamflow is determined.
If the orientation is not orthogonal the integrals are the result of the inner product of the velocity vector \(\bar V\) and the area vector \(\bar {dA}\)
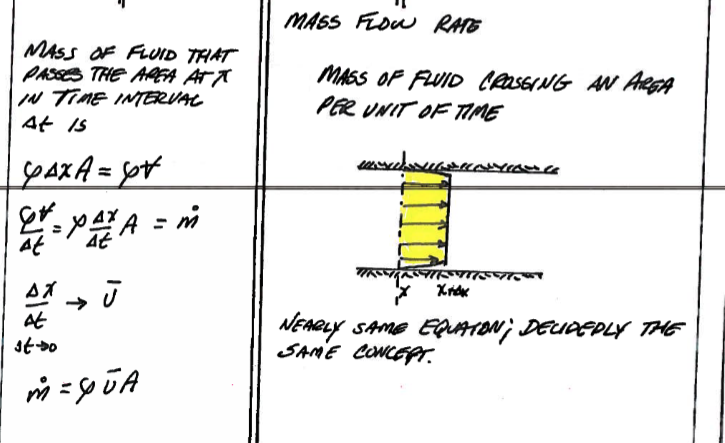
The mass flow rate is the product of the volumetric rate and the fluid density
As with volume, the mass flows also are obtained by inner products as:
Example: Flow in a Rectangular Conduit¶
Example: Flow in a Triangular Conduit¶
