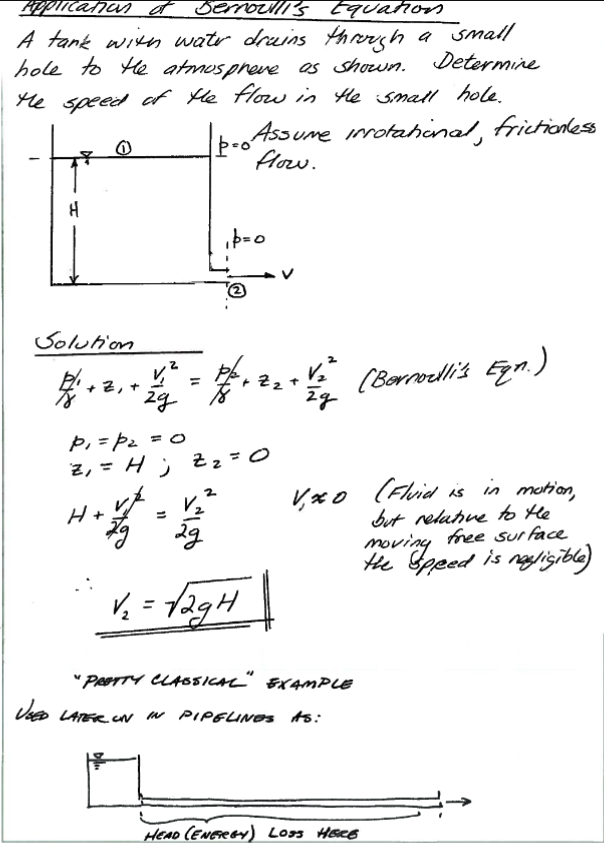
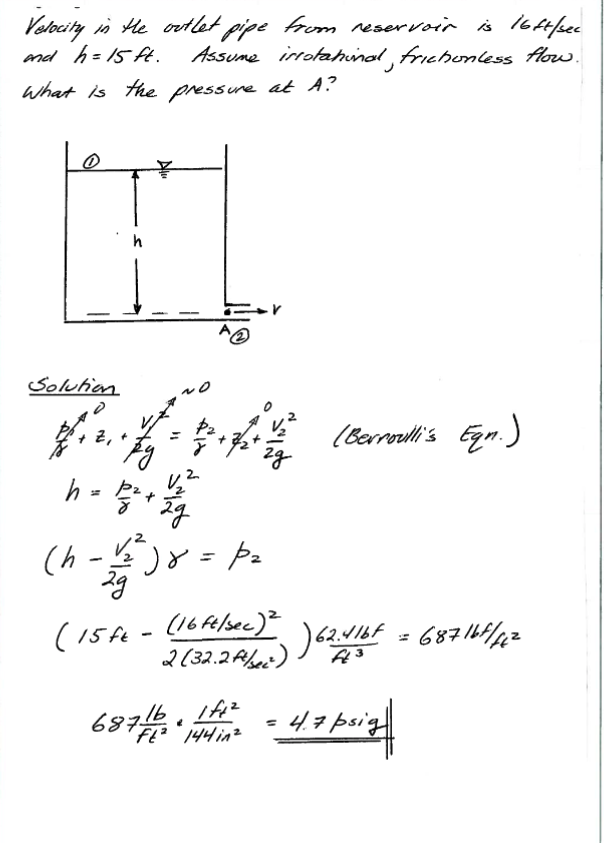
Bernoulli Equation Applications (pp. 220-232)¶
Recall from last time the equation of
steady (\(\frac{\partial}{\partial t} = 0\))
inviscid (\( \frac{\partial V}{\partial y} = 0\))
gravity vector is down (\(-z\))
incompressible (\(\rho = constant\))
irrotational (\(curl(V)=0\))
Results in
\( \frac{p_1}{\rho g} + \frac{V_1^2}{2g} + z_1 = \frac{p_2}{\rho g} + \frac{V_2^2}{2g} + z_2 \)
Below are some examples illustrating its use
Example: How high will a fountain go?¶
Consider the fountains at a resort. What kind of pressures and velocities are required to make the show happen?
Here’s a related problem that could form the basis of fountain design.
Identify the problem solving steps employed