Liquid Properties (pp. 28-31)¶
A liquid is one kind of fluid, but it has a few added properties that are important. One such property is surface tension, \(\sigma\).
Surface tension is the force per unit area required to separate two fluids. It is measured with a ring tensiometer https://en.wikipedia.org/wiki/Du_No%C3%BCy_ring_method, and a few other ways. Dimensionally it is a force per unit length, and is one reason why liquids can rise up capillary tubes, or into porous materials (like a sponge). Surface tension controls how liquids spread or bead up on a surface.
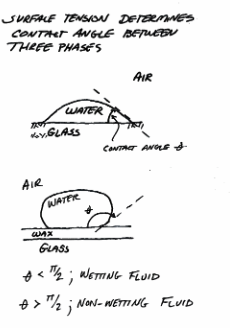
Fig. 29 Wetting and non-wetting fluid-fluid-solid systems.¶
Fig. 29 is a schematic of a wetting and non-wetting drop of fluid onto a surface.
Capillary Rise¶
We can explain capillary rise using a force-balance and the concepts of wetting and non-wetting fluids.
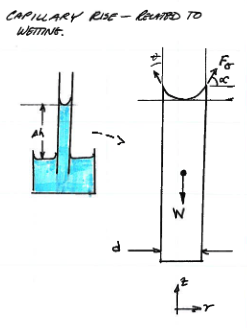
Fig. 30 Schematic of capillary tube¶

Fig. 31 Force balance analysis of portion above free surface.¶
Note
Some of the intermediate algebra is shown below to illustrate the terms that are cancelled. Many equations in the book are shown without intermediate steps; its up to you to trust explicitly, or check the intermediate steps yourselves - textbooks are a bit more reliable than Facebook for facts, but not much (even this notebook should be held suspect until you check the work for errors and ommissions!)
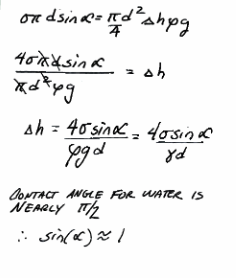
Fig. 32 Intermediate algebra¶
Fig. 32 is some of the intermediate algebra for capillary tubes.
Using our equations and knowledge of contact angle for water in the note above we can calculate the rise in a capillary tube.
Example 3 - Capillary Tube¶
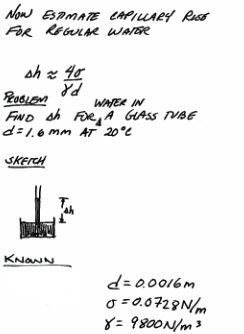
Fig. 33 Intermediate algebra¶
Fig. 33 is a brief problem statement, sketch, and list of known values.

Fig. 34 Intermediate algebra¶
Fig. 34 is the remainder of the solution, with a list of unknowns, the governing equation, and worked out solution. Notice the solution protocol is still followed but greatly simplified in this example.
