Contents

ENGR 1330 Computational Thinking with Data Science

Copyright © 2021 Theodore G. Cleveland and Farhang Forghanparast

Last GitHub Commit Date:

14: Visual display of data

This lesson is a prelude to the matplotlib external module package, used to construct line charts, scatter plots, bar charts, box plot, and histograms. matplotlib is used herein to generate some different plots; with additional detail in a subseqent lesson.

  • plot types

  • plot uses

  • plot conventions

Objectives

  • List common plot types and their uses

  • Identify the parts of a line (or scatter) plot

  1. Define the ordinate, abscissa

  2. Define independent and dependent variables

  • Define how to plot experimental data (observations) and theoretical data (model)

  1. Marker conventions

  2. Line conventions

  3. Legends

About matplotlib

Quoting from: https://matplotlib.org/tutorials/introductory/pyplot.html#sphx-glr-tutorials-introductory-pyplot-py

matplotlib.pyplot is a collection of functions that make matplotlib work like MATLAB. Each pyplot function makes some change to a figure: e.g., creates a figure, creates a plotting area in a figure, plots some lines in a plotting area, decorates the plot with labels, etc.

In matplotlib.pyplot various states are preserved across function calls, so that it keeps track of things like the current figure and plotting area, and the plotting functions are directed to the current axes (please note that “axes” here and in most places in the documentation refers to the axes part of a figure and not the strict mathematical term for more than one axis).

Computational thinking (CT) concepts involved are:

  • Decomposition : Break a problem down into smaller pieces; separating plotting from other parts of analysis simplifies maintenace of scripts

  • Abstraction : Pulling out specific differences to make one solution work for multiple problems; wrappers around generic plot calls enhances reuse

  • Algorithms : A list of steps that you can follow to finish a task; Often the last step and most important to make professional graphics to justify the expense (of paying you to do engineering) to the client.

Graphics Conventions for Plots

Note

This section needs to have graphics replaced with author generated examples in future editions

Terminology: Ordinate, Abscissa, Dependent and Independent Variables

A few terms are used in describing plots:

  • Abscissa – the horizontal axis on a plot (the left-right axis)

  • Ordinate – the vertical axis on a plot (the up-down axis)

A few terms in describing data models

  • Independent Variable (Explainatory, Predictor, Feature, …) – a variable that can be controlled/manipulated in an experiment or theoretical analysis

  • Dependent Variable (Response, Prediction, …) – the variable that measured/observed as a function of the independent variable

Plotting convention in most cases assigns explainatory variables to the horizontal axis (e.g. Independent variable is plotted on the Abscissa) and the response variable(s) to the vertical axis (e.g. Dependent Variable is plotted on the Ordinate)

Conventions for Proper Plots

  • Include a title OR a caption with a brief description of the plot

  • Label both axes clearly

    • Include the variable name, the variable, and the unit in each label

  • If possible, select increments for both the x and y axes that provide for easy interpolation

  • Include gridlines

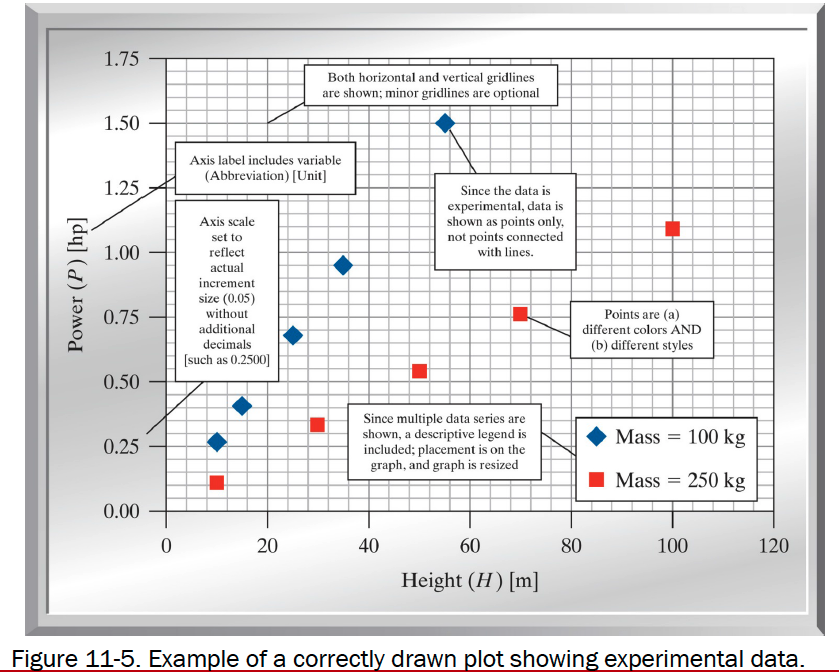
  • Show experimental measurements as symbols

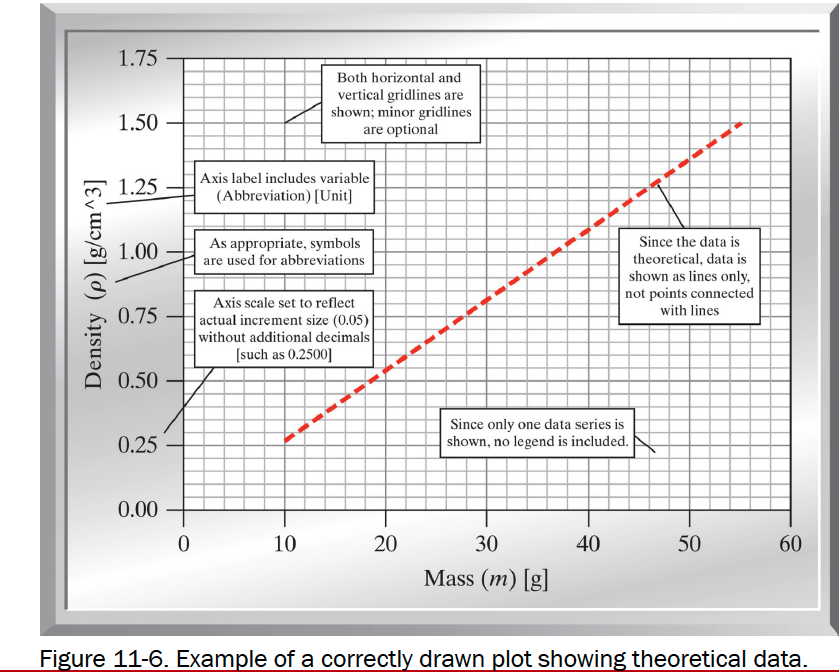
  • Show model (theoretical) relationships as lines

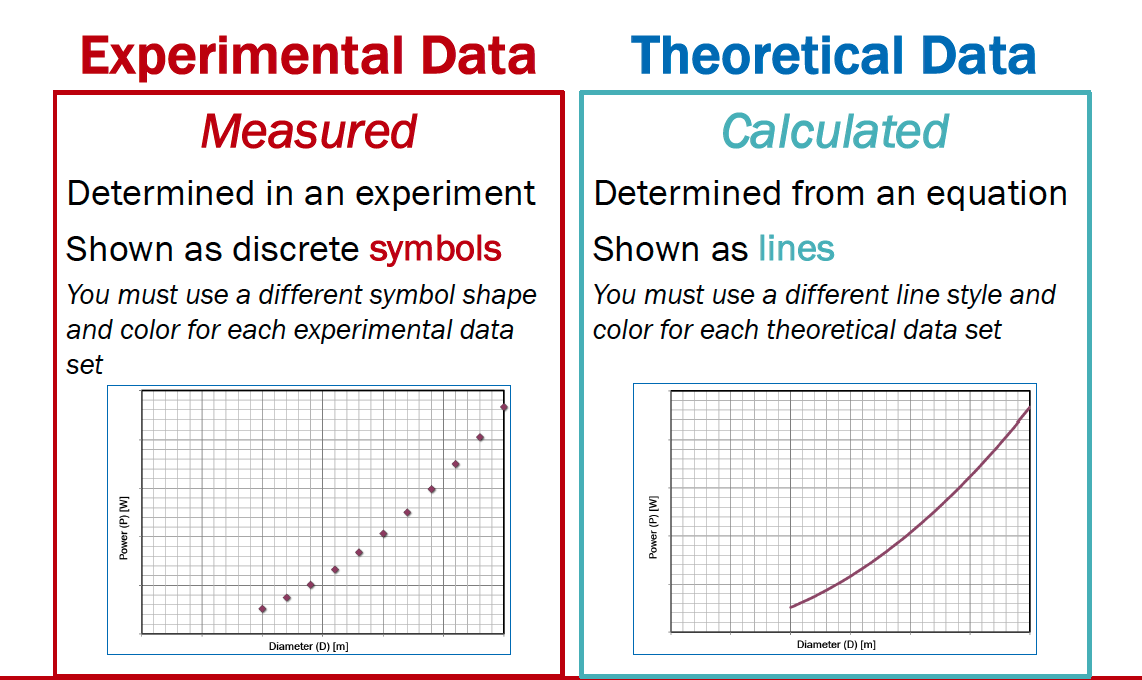
  • Use portrait orientation when making your plot

  • Make the plot large enough to be easily read

  • If more than one experimental dataset is plotted

    • Use different shapes for each dataset

    • Use different colors for each dataset

    • Include a legend defining the datasets

Line Charts using matplotlib

A line chart or line plot or line graph or curve chart is a type of chart which displays information as a series of data points called ‘markers’ connected by straight line segments.

It is a basic type of chart common in many fields. It is similar to a scatter plot (below) except that the measurement points are ordered (typically by their x-axis value) and joined with straight line segments.

A line chart is often used to visualize a trend in data over intervals of time – a time series – thus the line is often drawn chronologically.

The x-axis spacing is sometimes tricky, hence line charts can unintentionally decieve - so be careful that it is the appropriate chart for your application.

Example

Consider the experimental data below

Elapsed Time (s)

Speed (m/s)

0

0

1.0

3

2.0

7

3.0

12

4.0

20

5.0

30

6.0

45.6

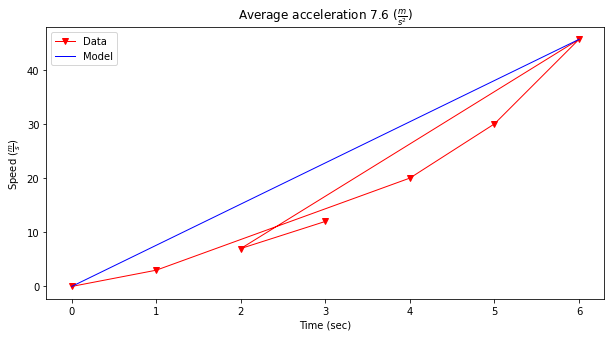
Show the relationship between time and speed. Is the relationship indicating acceleration? How much?

# import the package
from matplotlib import pyplot as plt

# Create two lists; time  and speed.
time = [0,1.0,2.0,3.0,4.0,5.0,6.0]
speed = [0,3,7,12,20,30,45.6]

# Create a line chart of speed on y axis and time on x axis
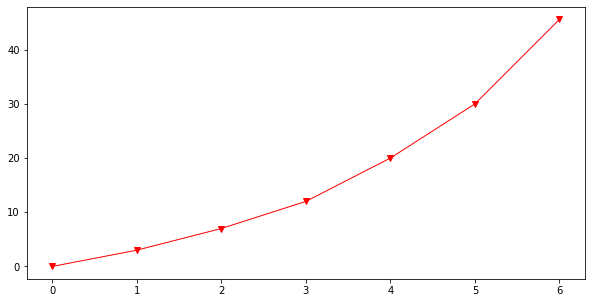
mydata = plt.figure(figsize = (10,5)) # build a square drawing canvass from figure class
plt.plot(time, speed, c='red', marker='v',linewidth=1) # basic line plot
plt.show()
../../_images/lesson14_18_0.png 
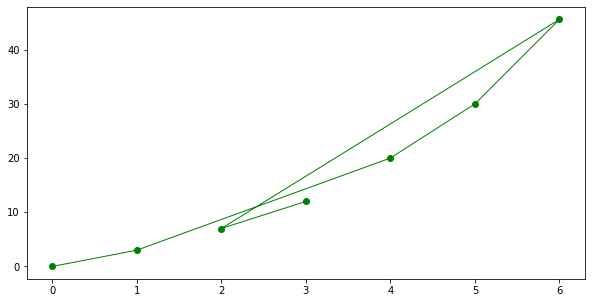
time = [0,1.0,4.0,5.0,6.0,2.0,3.0]
speed = [0,3,20,30,45.6,7,12]
# Create a line chart of speed on y axis and time on x axis
mydata = plt.figure(figsize = (10,5)) # build a square drawing canvass from figure class
plt.plot(time, speed, c='green', marker='o',linewidth=1) # basic line plot
plt.show()
../../_images/lesson14_19_0.png 
# Estimate acceleration (naive)
dvdt = (max(speed) - min(speed))/(max(time)-min(time))
plottitle = 'Average acceleration %.1f' % (dvdt) + r' ($\frac{m}{s^2}$)'
seriesnames = ['Data','Model']
modely = [min(speed),max(speed)]
modelx = [min(time),max(time)]
mydata = plt.figure(figsize = (10,5)) # build a square drawing canvass from figure class
plt.plot(time, speed, c='red', marker='v',linewidth=1) # basic line plot
plt.plot(modelx, modely, c='blue',linewidth=1) # basic line plot
plt.xlabel('Time (sec)')
plt.ylabel('Speed '+r'($\frac{m}{s}$)')
plt.legend(seriesnames)
plt.title(plottitle)
plt.show()
../../_images/lesson14_20_0.png

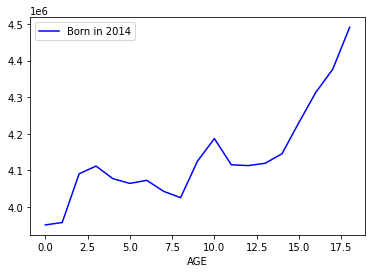
Line Charts in Pandas

The next few examples use graphics in pandas. The example below uses a database table from census_18.csv

import pandas as pd

df = pd.read_csv('census_18.csv')
df.head()
AGE 2010 2014
0 0 3951330 3949775
1 1 3957888 3949776
2 2 4090862 3959664
3 3 4111920 4007079
4 4 4077551 4005716 
df.plot.line(x="AGE", y="2010", label="Born in 2014", c="blue")

<AxesSubplot:xlabel='AGE'>
../../_images/lesson14_23_1.png 
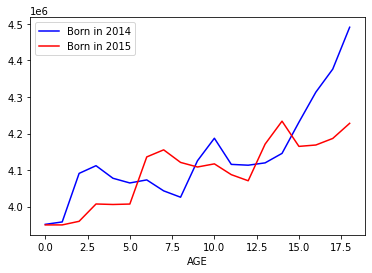
ax = df.plot.line(x="AGE", y="2010", label="Born in 2014", c="blue")
df.plot.line(x="AGE", y="2014", label="Born in 2015", c="red", ax=ax)

<AxesSubplot:xlabel='AGE'>
../../_images/lesson14_24_1.png 
import matplotlib.pyplot as plt

age = df['AGE']
born2010 = df['2010']
born2014 = df['2014']

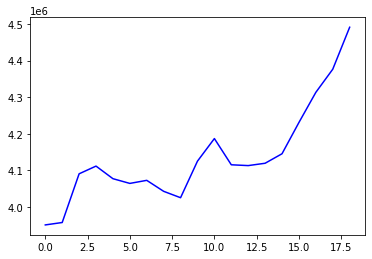
plt.plot(age, born2010, c='blue')
plt.show()
../../_images/lesson14_25_0.png 
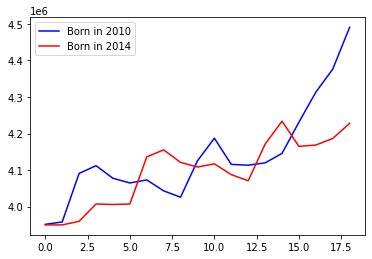
plt.plot(age, born2010, c='blue', label='Born in 2010')
plt.plot(age, born2014, c='red', label='Born in 2014')
plt.legend()
plt.show()
../../_images/lesson14_26_0.png

References

  1. Grus, Joel (2015-04-14). Data Science from Scratch: First Principles with Python (Kindle Locations 1190-1191). O’Reilly Media. Kindle Edition.

  2. Call Expressions in “Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science” https://www.inferentialthinking.com/chapters/03/3/Calls.html

  3. Functions and Tables in “Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science” https://www.inferentialthinking.com/chapters/08/Functions_and_Tables.html

  4. Visualization in “Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science” https://www.inferentialthinking.com/chapters/07/Visualization.html

  5. Documentation; The Python Standard Library; 9. Numeric and Mathematical Modules https://docs.python.org/2/library/math.html

  6. https://matplotlib.org/gallery/lines_bars_and_markers/horizontal_barchart_distribution.html?highlight=horizontal bar chart

  7. https://www.geeksforgeeks.org/bar-plot-in-matplotlib/

Addendum (Scripts that are Interactive)

Note

The addendum is intended for in-class demonstration

# python script to illustrate plotting
# CODE BELOW IS ADAPTED FROM:
# Grus, Joel (2015-04-14). Data Science from Scratch: First Principles with Python
# (Kindle Locations 1190-1191). O'Reilly Media. Kindle Edition. 
#
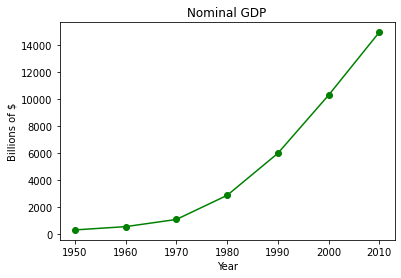
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()

years = [1950, 1960, 1970, 1980, 1990, 2000, 2010]  # define one list for years
gdp = [300.2, 543.3, 1075.9, 2862.5, 5979.6, 10289.7, 14958.3] # and another one for Gross Domestic Product (GDP)
plt.plot( years, gdp, color ='green', marker ='o', linestyle ='solid') # create a line chart, years on x-axis, gdp on y-axis
                                                                       # what if "^", "P", "*" for marker?
                                                                       # what if "red" for color?  
                                                                       # what if "dashdot", '--' for linestyle?  


plt.title("Nominal GDP")# add a title
plt.ylabel("Billions of $")# add a label to the x and y-axes
plt.xlabel("Year")
plt.show() # display the plot
../../_images/lesson14_29_0.png

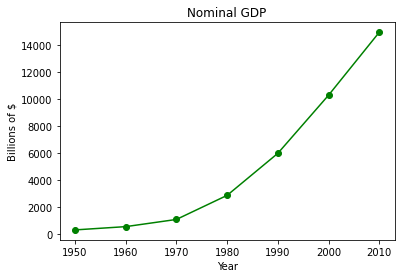
Now lets put the plotting script into a function so we can make line charts of any two numeric lists

def plotAline(list1,list2,strx,stry,strtitle): # plot list1 on x, list2 on y, xlabel, ylabel, title
    from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
    plt.plot( list1, list2, color ='green', marker ='o', linestyle ='solid') # create a line chart, years on x-axis, gdp on y-axis
    plt.title(strtitle)# add a title
    plt.ylabel(stry)# add a label to the x and y-axes
    plt.xlabel(strx)
    plt.show() # display the plot
    return #null return

# wrapper
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010]  # define two lists years and gdp
gdp = [300.2, 543.3, 1075.9, 2862.5, 5979.6, 10289.7, 14958.3]
print(type(years[0]))
print(type(gdp[0]))
plotAline(years,gdp,"Year","Billions of $","Nominal GDP")

<class 'int'>
<class 'float'>
../../_images/lesson14_32_1.png

Example

Use the plotting script and create a function that draws a straight line between two points.

    def Line():
    from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
    x1 = input('Please enter x value for point 1')
    y1 = input('Please enter y value for point 1')
    x2 = input('Please enter x value for point 2')
    y2 = input('Please enter y value for point 2')
    xlist = [x1,x2]
    ylist = [y1,y2]
    plt.plot( xlist, ylist, color ='orange', marker ='*', linestyle ='solid') 
    #plt.title(strtitle)# add a title
    plt.ylabel("Y-axis")# add a label to the x and y-axes
    plt.xlabel("X-axis")
    plt.show() # display the plot
    return #null return

Laboratory 14

Examine (click) Laboratory 15 as a webpage at Laboratory 14.html

Download (right-click, save target as …) Laboratory 15 as a jupyterlab notebook from Laboratory 14.ipynb

Exercise Set 14

Examine (click) Exercise Set 15 as a webpage at Exercise 14.html

Download (right-click, save target as …) Exercise Set 15 as a jupyterlab notebook at Exercise Set 14.ipynb