Contents

ENGR 1330 Computational Thinking with Data Science

Copyright © 2021 Theodore G. Cleveland and Farhang Forghanparast

Last GitHub Commit Date:

8: Vectors and Matrices (as lists)

  • The Matrix: A special data structure

  • Matrix Definition

  • Matrix Arithmetic

  • Multiply a matrix by a scalar .

  • Matrix addition (and subtraction)

  • Multiply a matrix

  • Identity matrix

  • Matrix Inverse

    • Gauss-Jordan method of finding \(A^{−1}\)

Objectives

  1. Demonstrate matrices as a list of lists

  2. Demonstrate matrix arithmetic using fundamental arithmetic and list manipulation

The Matrix: A special data structure

A matrix is a rectangular array of numbers:

Or more for our needs something like:

\( \begin{gather} \begin{pmatrix} 1 & 5 & 7 & 2\\ 2 & 9 & 17 & 5 \\ 11 & 15 & 8 & 3 \\ \end{pmatrix} \end{gather} \)

The size of a matrix is referred to in terms of the number of rows and the number of columns. The enclosing parenthesis are optional above, but become meaningful when writing multiple matrices next to each other. The above matrix is 3 by 4.

When we are discussing matrices we will often refer to specific numbers in the matrix. To refer to a specific element of a matrix we refer to the row number (i) and the column number (j). We will often call a specific element of the matrix, the \(a_{i,j}\) -th element of the matrix. For example \(a_{2,3}\) element in the above matrix is 17.

We have seen in Python that we would refer to the element as \(a_{matrix}[i][j]\) or whatever the name of the matrix is in the program; with the caveat that the elements start counting at 0. For instance in the matrix above \(a_{matrix}[0][0]\) contains the value 1.

A vector is really just a matrix with a single column, but are often treated as different kinds of entities. In python core, a matrix is simply a list of lists - each row is a list, and the matrix is a collection of rows. A vector is simply a collection (list) of elements (we can force a vector to be a matrix, but we would have a structure that builds a collection of single element lists)

For small matrices we can build them with explicit code; but larger ones are usually kept in files (hence the file handling lesson prior to this lesson). Also processing matrices as lists is ultimately cumbersome, so we will later (next lesson) employ the numpy package that greatly facilitates matrix manipulation - here we will learn about matrix manipulation for the pedagogcal aspect.

To complete this section, lets create the matrix above and access its contents.

amatrix = [[1 , 5 , 7 , 2],
           [2 , 9 , 17 , 5],
           [11 , 15 , 8 , 3]]
print('rows = ',len(amatrix),'cols = ',len(amatrix[0]))
for i in range(len(amatrix)): # print by row
    print(amatrix[i][:])

rows =  3 cols =  4
[1, 5, 7, 2]
[2, 9, 17, 5]
[11, 15, 8, 3]

Matrix Arithmetic

Analysis of many problems in engineering result in systems of simultaneous equations. We typically represent systems of equations with a matrix. For example the two- equation system,

\[\begin{split} \begin{gather} \begin{matrix} 2x_1 & ~+~~3x_2 \\ ~\\ 4x_1 & ~-~~3x_2 \\ \end{matrix} \begin{matrix} =~8\\ ~\\ =~-2\\ \end{matrix} \end{gather} \end{split}\]

Could be represented by set of vectors and matrices(Usually called vector-matrix form.
Additionally, a vector is really just a matrix with column rank = 1 (a single column matrix).)

\[\begin{split} \begin{gather} \mathbf{A} = \begin{pmatrix} 2 & ~3 \\ ~\\ 4 & -3 \\ \end{pmatrix} ~ \mathbf{x} = \begin{pmatrix} x_1\\ ~\\ x_2\\ \end{pmatrix} ~ \mathbf{b} = \begin{pmatrix} ~8\\ ~\\ -2\\ \end{pmatrix} \end{gather} \end{split}\]

and the linear system then written as

\[ \begin{gather} \mathbf{A} \cdot \mathbf{x} = \mathbf{b} \end{gather} \]

So the “algebra” is considerably simplified, at least for writing things, however we now have to be able to do things like multiplication (indicated by \( ~\cdot \)) as well as the concept of addition and subtraction, and division (multiplication by an inverse).

There are also several kinds of matrix multiplication – the inner (or dot) product as required by the linear system, the vector (cross product), the exterior (wedge), and outer (tensor) product are a few of importance in both mathematics and engineering.

Matrix Arithmetic

Multiply a matrix by a scalar

A scalar multiple of a matrix is simply each element of the matrix multiplied by the scalar value. Consider the matrix \(\mathbf{A}\) below.

\[\begin{split} \begin{gather} \mathbf{A}= \begin{pmatrix} 1 & 5 & 7 \\ 2 & 9 & 3 \\ 4 & 4 & 8 \\ \end{pmatrix} \end{gather} \end{split}\]

If the scalar is say 2, then \(2 \times \mathbf{A}\) is computed by doubling each element of \(\mathbf{A}\), as

\[\begin{split} \begin{gather} 2\mathbf{A}= \begin{pmatrix} 2 & 10 & 14\\ 4 & 18 & 6 \\ 8 & 8 & 16 \\ \end{pmatrix} \end{gather} \end{split}\]
# interactive input - copy+paste into a notebook and run
amatrix = [[1 , 5 , 7 ],
           [2 , 9 , 3],
           [4 , 4 , 8 ]]
MyScalar = input("Enter scalar value for multiply matrix \n")
MyScalar = float(MyScalar)  # force a float
# now perform element-by-element multiplication
for i in range(0,len(amatrix),1):
   for j in range(0,len(amatrix[0]),1):
       amatrix[i][j] = MyScalar * amatrix[i][j] # this will change contents of amatrix
for i in range(len(amatrix)): # print by row
    print(amatrix[i][:])

Matrix addition (and subtraction)

Matrix addition and subtraction are also element-by-element operations. In order to add or subtract two matrices they must be the same size and shape. This requirement means that they must have the same number of rows and columns. To add or subtract a matrix we simply add or subtract the corresponding elements from each matrix.

For example consider the two matrices \(\mathbf{A}\) and \(\mathbf{B}\) below

\[\begin{split} \begin{gather} \mathbf{A}= \begin{pmatrix} 1 & 5 & 7 \\ 2 & 9 & 3 \\ \end{pmatrix} ~ \mathbf{B}= \begin{pmatrix} 3 & -2 & 1 \\ -2 & 1 & 1 \\ \end{pmatrix} \end{gather} \end{split}\]

For example the sum of these two matrices is the matrix named \(\mathbf{A+B}\), shown below:

\[\begin{split} \begin{gather} \mathbf{A+B}= \begin{pmatrix} 1+3 & 5-2 & 7+1 \\ 2-2 & 9+1 & 3+1 \\ \end{pmatrix} = \begin{pmatrix} 4 & 3 & 8 \\ 0 & 10 & 4 \\ \end{pmatrix} \end{gather} \end{split}\]

Now to do the operation in Python, we need to read in the matrices, perform the addition, and write the result.

amatrix = [[1 , 5 , 7 ],
           [2 , 9 , 3]]
bmatrix = [[3 , -2 , 1 ],
           [-2 , 1 , 1]]
cmatrix = [[0 for j in range(len(amatrix[0]))] for i in range(len(amatrix))] # 2D list to receive input; explicit sizing
for i in range(len(cmatrix)): # print by row
    print(cmatrix[i][:])
print("-----")
for i in range(len(amatrix)):
    for j in range(len(amatrix[0])):
        cmatrix[i][j]= amatrix[i][j] + bmatrix[i][j]
for i in range(len(cmatrix)): # print by row
    print(cmatrix[i][:])

[0, 0, 0]
[0, 0, 0]
-----
[4, 3, 8]
[0, 10, 4]

In the code example above I added a third matrix to store the result – generally we don’t want to clobber existing matrices; Also notice the construction of the third matrix, because I should know the size I can use a double constructor-type iterator assignment to create and fill the matrix with zeros in the correct size and shape.

Sometimes it doesn’t matter if we clobber an existing matrix in which case something like:

amatrix = [[1 , 5 , 7 ],
           [2 , 9 , 3]]
bmatrix = [[3 , -2 , 1 ],
           [-2 , 1 , 1]]
for i in range(len(amatrix)):
    for j in range(len(amatrix[0])):
        amatrix[i][j]= amatrix[i][j] + bmatrix[i][j] # amatrix is replaced with the sum
for i in range(len(cmatrix)): # print by row
    print(amatrix[i][:])

[4, 3, 8]
[0, 10, 4]

would work just fine.

Subtraction is performed in a similar fashion, except the subtraction operator is used.

amatrix = [[1 , 5 , 7 ],
           [2 , 9 , 3]]
bmatrix = [[3 , -2 , 1 ],
           [-2 , 1 , 1]]
cmatrix = [[0 for j in range(len(amatrix[0]))] for i in range(len(amatrix))] # 2D list to receive input; explicit sizing
for i in range(len(amatrix)):
    for j in range(len(amatrix[0])):
        cmatrix[i][j]= amatrix[i][j] - bmatrix[i][j] # subtract bmatrix from amatrix
for i in range(len(cmatrix)): # print by row
    print(cmatrix[i][:])

[-2, 7, 6]
[4, 8, 2]

Matrix multiplication

Matrix multiplication is more complex than addition and subtraction. There are several types of multiplication with respect to matrices, usually when matrix multiplication is mentioned without further qualification ,the implied meaning is the inner (or dot) product of the matrix and a vector (or another matrix) of the correct shapes.

If two matrices such as a matrix \(\mathbf{A}\) (size L x m) and a matrix \(\mathbf{B}\) ( size m x n) are multiplied together, the resulting matrix \(\mathbf{C}\) has a size of L x n. The order of multiplication of matrices is important (Matrix multiplication is not transitive; \(\mathbf{A}~\mathbf{B} ~\ne~ \mathbf{B}~\mathbf{A}\).).

To obtain \(\mathbf{C}\) = \(\mathbf{A}\) \(\mathbf{B}\), the number of columns in \(\mathbf{A}\) must be the same as the number of rows in \(\mathbf{B}\). In order to carry out the matrix operations for multiplication of matrices, the \(i,j\)-th element of \(\mathbf{C}\) is simply equal to the scalar (dot or inner) product of row \(i\) of \(\mathbf{A}\) and column \(j\) of \(\mathbf{B}\).

Consider the example below

\[\begin{split} \begin{gather} \mathbf{A}= \begin{pmatrix} 1 & 5 & 7 \\ 2 & 9 & 3 \\ \end{pmatrix} ~ \mathbf{B}= \begin{pmatrix} 3 & -2 \\ -2 & 1 \\ 1 & 1 \\ \end{pmatrix} \end{gather} \end{split}\]

Suppose we wish to compute the inner product \(\mathbf{A}~\mathbf{B}\)

First, we would evaluate if the operation is even possible, \(\mathbf{A}\) has two rows and three columns. \(\mathbf{B}\) has three rows and two columns.

By our implied multiplication “rules” for the multiplication to be defined the first matrix must have the same number of rows as the second matrix has columns (in this case it does), and the result matrix will have the same number of rows as the first matrix, and the same number of columns as the second matrix (in this case the result will be a 2X2 matrix).

\[\begin{split} \begin{gather} \mathbf{C}=\mathbf{A}\mathbf{B}= \begin{pmatrix} c_{1,1} & c_{1,2} \\ c_{2,1} & c_{2,2} \\ \end{pmatrix} \end{gather} \end{split}\]

And each element of \(\mathbf{C}\) is the dot product of the row vector of \(\mathbf{A}\) and the column vector of \(\mathbf{B}\).

\[\begin{split} \begin{gather} c_{1,1} = \begin{pmatrix} 1 & 5 & 7 \\ \end{pmatrix} \cdot \begin{pmatrix} 3 \\ -2 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} (1)(3) +(5)(-2) + (7)(1)\\ \end{pmatrix} = 0 \end{gather} \end{split}\]
\[\begin{split} \begin{gather} c_{1,2} = \begin{pmatrix} 1 & 5 & 7 \\ \end{pmatrix} \cdot \begin{pmatrix} -2 \\ 1 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} (1)(-2) +(5)(1) + (7)(1)\\ \end{pmatrix} = 10 \end{gather} \end{split}\]
\[\begin{split} \begin{gather} c_{2,1} = \begin{pmatrix} 2 & 9 & 3 \\ \end{pmatrix} \cdot \begin{pmatrix} 3 \\ -2 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} (2)(3) +(9)(-2) + (3)(1)\\ \end{pmatrix} = -9 \end{gather} \end{split}\]
\[\begin{split} \begin{gather} c_{2,2} = \begin{pmatrix} 2 & 9 & 3 \\ \end{pmatrix} \cdot \begin{pmatrix} -2 \\ 1 \\ 1 \\ \end{pmatrix} = \begin{pmatrix} (2)(-2) +(9)(1) + (3)(1)\\ \end{pmatrix} = 8 \end{gather} \end{split}\]

Making the substitutions results in :

\[\begin{split} \begin{gather} \mathbf{C}=\mathbf{A}\mathbf{B}= \begin{pmatrix} 0 & 10 \\ -9 & 8 \\ \end{pmatrix} \end{gather} \end{split}\]

So in an algorithmic sense we will have to deal with three matrices, the two source matrices and the destination matrix.
We will also have to manage element-by-element multiplication and be able to correctly store through rows and columns.

Here is the process in a script. The bmatrix object must be a 2D list, or it won’t work

amatrix = [[1 , 5 , 7 ],
           [2 , 9 , 3]]
bmatrix = [[3 , -2 ], 
           [-2 , 1 ],
           [ 1 , 1]]
# destination matrix, rows count same a amatrix, columns count same as bmatrix
cmatrix = [[0 for j in range(len(bmatrix[0]))] for i in range(len(amatrix))] # 2D list to receive input; explicit sizing
# now for the multiplication
for i in range(0,len(amatrix)):
    for j in range(0,len(bmatrix[0])):
        for k in range(0,len(amatrix[0])):
            cmatrix[i][j]=cmatrix[i][j]+amatrix[i][k]*bmatrix[k][j]
for i in range(len(cmatrix)): # print by row
    print(cmatrix[i][:])

[0, 10]
[-9, 8]

Identity matrix

In computational linear algebra we often need to make use of a special matrix called the “Identity Matrix”.
The Identity Matrix is a square matrix with all zeros except the \(i,i\)-th element (diagonal) which is equal to 1:

\[\begin{split} \begin{gather} \mathbf{I}_{3\times3}= \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{pmatrix} \end{gather} \end{split}\]

Usually we don’t bother with the size subscript used above and just stipulate that the matrix is sized as appropriate.

Multiplying any matrix by (a correctly sized) identity matrix results in no change in the matrix.

\(\mathbf{I}\mathbf{A} = \mathbf{A}\)

Using our script above

amatrix = [[1 , 5 , 7 ],
           [2 , 9 , 3],
           [4 , 4 , 8 ]]
print('A matrix')
for i in range(len(amatrix)): # print by row
    print(amatrix[i][:])
bmatrix = [[1 , 0 , 0 ],
           [0 , 1 , 0],
           [0 , 0 , 1 ]]
print('B matrix')
for i in range(len(bmatrix)): # print by row
    print(bmatrix[i][:])
# destination matrix, rows count same a amatrix, columns count same as bmatrix
cmatrix = [[0 for j in range(len(bmatrix[0]))] for i in range(len(amatrix))] # 2D list to receive input; explicit sizing
# now for the multiplication
for i in range(0,len(amatrix)):
    for j in range(0,len(bmatrix[0])):
        for k in range(0,len(amatrix[0])):
            cmatrix[i][j]=cmatrix[i][j]+amatrix[i][k]*bmatrix[k][j]
print('C = AB matrix')
for i in range(len(cmatrix)): # print by row
    print(cmatrix[i][:])

A matrix
[1, 5, 7]
[2, 9, 3]
[4, 4, 8]
B matrix
[1, 0, 0]
[0, 1, 0]
[0, 0, 1]
C = AB matrix
[1, 5, 7]
[2, 9, 3]
[4, 4, 8]

Matrix Inverse

In many practical computational and theoretical operations we employ the concept of the inverse of a matrix. The inverse is somewhat analogous to “dividing” by the matrix.
Consider our linear system

\[ \begin{gather} \mathbf{A} \cdot \mathbf{x} = \mathbf{b} \end{gather} \]

If we wished to solve for \(\mathbf{x}\) we would “divide” both sides of the equation by \(\mathbf{A}\). Instead of division (which is essentially left undefined for matrices) we instead multiply by the inverse of the matrix (The matrix inverse is the multiplicative inverse of the matrix – we are defining a division operation, just calling it something else.).

The inverse of a matrix \(\mathbf{A}\) is denoted by \(\mathbf{A}^{-1}\) and by definition is a matrix such that when \(\mathbf{A}^{-1}\) and \(\mathbf{A}\) are multiplied together, the identity matrix \(\mathbf{I}\) results. e.g. \(\mathbf{A}^{-1} \mathbf{A} = \mathbf{I}\)

Lets consider the matrixes below

\[\begin{split} \begin{gather} \mathbf{A}= \begin{pmatrix} 2 & 3 \\ 4 & -3 \\ \end{pmatrix} \end{gather} \end{split}\]
\[\begin{split} \begin{gather} \mathbf{A}^{-1}= \begin{pmatrix} \frac{1}{6} & \frac{1}{6} \\ ~\\ \frac{2}{9} & -\frac{1}{9} \\ \end{pmatrix} \end{gather} \end{split}\]

Note

Here we have not actually shown how to invert a matrix, but we can test if two matrices are inversions of each other by taking their produce and seeing if it is an identity matrix.

We can check that the matrices are indeed inverses of each other using our Python code, performing the multiplication and then report the result. The result is the identity matrix regardless of the order of operation.

amatrix = [[2 ,  3 ],
           [4 , -3 ]]
print('A matrix')
for i in range(len(amatrix)): # print by row
    print(amatrix[i][:])
bmatrix = [[1/6 , 1/6 ],
           [2/9 , -1/9]]
print('A-inverse matrix')
for i in range(len(bmatrix)): # print by row
    print(bmatrix[i][:])
# destination matrix, rows count same a amatrix, columns count same as bmatrix
cmatrix = [[0 for j in range(len(bmatrix[0]))] for i in range(len(amatrix))] # 2D list to receive input; explicit sizing
# now for the multiplication
for i in range(0,len(amatrix)):
    for j in range(0,len(bmatrix[0])):
        for k in range(0,len(amatrix[0])):
            cmatrix[i][j]=cmatrix[i][j]+amatrix[i][k]*bmatrix[k][j]
print('C = A*A-inverse matrix')
for i in range(len(cmatrix)): # print by row
    print(cmatrix[i][:])

A matrix
[2, 3]
[4, -3]
A-inverse matrix
[0.16666666666666666, 0.16666666666666666]
[0.2222222222222222, -0.1111111111111111]
C = A*A-inverse matrix
[1.0, 0.0]
[0.0, 1.0]

Gauss-Jordan method of finding \(\mathbf{A}^{-1}\) (Optional)

Note

This section is presented as an introduction to algorithms/recipes for matrix inversion. The method here is gaussian-elimination which is ungodly slow (computationally), requires non-zero diagional elements ,and almost infinite-precision artithmetic being approximated. In practice other methods would likely be more useful.

A good source of practical algorithms is Numerical Recipies

There are a number of methods that can be used to find the inverse of a matrix using elementary row operations.

An elementary row operation is any one of the three operations listed below:

  1. Multiply or divide an entire row by a constant.

  2. Add or subtract a multiple of one row to/from another.

  3. Exchange the position of any 2 rows.

The Gauss-Jordan method of inverting a matrix can be divided into 4 main steps. In order to find the inverse we will be working with the original matrix, augmented with the identity matrix – this new matrix is called the augmented matrix (because no-one has tried to think of a cooler name yet).

\( \begin{gather} \mathbf{A} | \mathbf{I} = \begin{pmatrix} 2 & 3 & | & 1 & 0 \\ 4 & -3 & | & 0 & 1 \\ \end{pmatrix} \end{gather} \)

We will perform elementary row operations based on the left partition to convert it to an identity matrix – we perform the same operations on the right partition and the result when we are done is the inverse of the original matrix.

So here goes – in the theory here, we also get to do infinite-precision arithmetic, no rounding/truncation errors.

Divide row one by the \(a_{1,1}\) value to force a \(1\) in the \(a_{1,1}\) position. This is elementary row operation 1 in our list above.

\[\begin{split} \begin{gather} \mathbf{A} | \mathbf{I} = \begin{pmatrix} 2/2 & 3/2 & | & 1/2 & 0 \\ 4 & -3 & | & 0 & 1 \\ \end{pmatrix} = \begin{pmatrix} 1 & 3/2 & | & 1/2 & 0 \\ 4 & -3 & | & 0 & 1 \\ \end{pmatrix} \end{gather} \end{split}\]

For all rows below the first row, replace \(row_j\) with \(row_j - a_{j,1}*row_1\). This happens to be elementary row operation 2 in our list above.

\[\begin{split} \begin{gather} \mathbf{A} | \mathbf{I} = \begin{pmatrix} 1 & 3/2 & | & 1/2 & 0 \\ 4 - 4(1) & -3 - 4(3/2) & | & 0-4(1/2) & 1-4(0) \\ \end{pmatrix} = \begin{pmatrix} 1 & 3/2 & | & 1/2 & 0 \\ 0 & -9 & | & -2 & 1 \\ \end{pmatrix} \end{gather} \end{split}\]

Now multiply \(row_2\) by \( \frac{1}{ a_{2,2}} \). This is again elementary row operation 1 in our list above.

\[\begin{split} \begin{gather} \mathbf{A} | \mathbf{I} = \begin{pmatrix} 1 & 3/2 & | & 1/2 & 0 \\ 0 & -9/-9 & | & -2/-9 & 1/-9 \\ \end{pmatrix} = \begin{pmatrix} 1 & 3/2 & | & 1/2 & 0 \\ 0 & 1 & | & 2/9 & -1/9 \\ \end{pmatrix} \end{gather} \end{split}\]

For all rows above and below this current row, replace \(row_j\) with \(row_j - a_{2,2}*row_2\). This happens to again be elementary row operation 2 in our list above. What we are doing is systematically converting the left matrix into an identity matrix by multiplication of constants and addition to eliminate off-diagonal values and force 1 on the diagonal.

\[\begin{split} \begin{gather} \mathbf{A} | \mathbf{I} = \\ \begin{pmatrix} 1 & 3/2 - (3/2)(1) & | & 1/2 - (3/2)(2/9) & 0-(3/2)(-1/9) \\ 0 & 1 & | & 2/9 & -1/9 \\ \end{pmatrix} = \\ \begin{pmatrix} 1 & 0 & | & 1/6 & 1/6 \\ 0 & 1 & | & 2/9 & -1/9 \\ \end{pmatrix} \end{gather} \end{split}\]

As far as this example is concerned we are done and have found the inverse. With more than a 2X2 system there will be many operations moving up and down the matrix to eliminate the off-diagonal terms.

So the next logical step is to build an algorithm to perform these operations for us.

The code for inversion is a bit long, but is included as a monolithic block so we dont break things.

Note

Naturally we will need the files these are downloaded from :

The first part reads in the matrix from a file named “A.txt”, and then builds some workspaces for the inversion process. One of the workspaces is a matrix called “bmatrix” which is an identity matrix and is also the augmented portion of the system depicted in the 2X2 example. The actual inverse gets stored in a matrix named “xmatrix”, which is really a column-by-column collection of solutions to a linear system where the right hand side is the different columns of the identity matrix.

# InvertASystem.py
# Code to read A and b
# Then solve Ax = b for x by Gaussian elimination with back substitution
#
print ("invert a matrix by Gaussian elimination - requires diagionally dominant system")

amatrix = [] # null list to store matrix reads
rowNumA = 0
colNumA = 0
afile = open("A.txt","r") # connect and read file for MATRIX A 
for line in afile:
    amatrix.append([float(n) for n in line.strip().split()])
    rowNumA += 1
afile.close() # Disconnect the file
colNumA = len(amatrix[0])
bvector = [0 for i in range(rowNumA)] # will use as rhs in linear solver
cmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
dmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
bmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
xmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
xvector = [0 for i in range(rowNumA)]
for i in range(0,rowNumA,1):
    bmatrix[i][i] = 1.0 #augmented partition
    print (amatrix[i][0:colNumA], bmatrix[i][0:colNumA])
print ("-----------------------------")
dmatrix = [[amatrix[i][j] for j in range(colNumA)]for i in range(rowNumA)] # copy amatrix into dmatrix  -- this is a static copy

# outer wrapper loop
for jcol in range(rowNumA):
    xvector = [0 for i in range(rowNumA)] # empty column of the inverse

    for i in range(rowNumA):
        bvector[i]=bmatrix[i][jcol]
    amatrix = [[dmatrix[i][j] for j in range(colNumA)]for i in range(rowNumA)]
    cmatrix = [[dmatrix[i][j] for j in range(colNumA)]for i in range(rowNumA)]

    for k in range(rowNumA-1): # build the diagonal -- assume diagonally dominant
        l = k+1
        for i in range(l,rowNumA):
            for j in range(colNumA):
                cmatrix[i][j]=amatrix[i][j]-amatrix[k][j]*amatrix[i][k]/amatrix[k][k]
            bvector[i] = bvector[i]-bvector[k]*amatrix[i][k]/amatrix[k][k]
            bmatrix[i][jcol] = bmatrix[i][jcol]-bmatrix[k][jcol]*amatrix[i][k]/amatrix[k][k]
        for i in range(rowNumA):
            for j in range(colNumA):
                amatrix[i][j] = cmatrix[i][j]
# gaussian reduction done
# now for the back substitution
    for k in range(rowNumA-1,-1,-1):
        sum = 0.0
        sum1 = 0.0
        for i in range(rowNumA):
            if i == k:
                continue 
            else:
                sum = sum + amatrix[k][i]*xvector[i]
                sum1 = sum1 + amatrix[k][i]*xmatrix[i][jcol]
            xvector[k]=(bvector[k]-sum)/amatrix[k][k]
            xmatrix[k][jcol]=(bmatrix[k][jcol]-sum1)/amatrix[k][k]
# end of wrapper
print ("[      A-Matrix          ]|[       A-Inverse        ]")
print ("_____________________________________________________")
for i in range(0,rowNumA,1):
    print (dmatrix[i][0:colNumA],"|", xmatrix[i][0:colNumA])
print ("_____________________________________________________")
ofile = open("A-Matrix.txt","w") # "w" clobbers content already there!
for i in range(0,rowNumA,1):
    message = '  '.join(map(repr, dmatrix[i][0:colNumA])) + "\n" 
    ofile.write(message)
ofile.close()
ofile = open("A-Inverse.txt","w") # "w" clobbers content already there!
for i in range(0,rowNumA,1):
    message = '  '.join(map(repr, xmatrix[i][0:colNumA])) + "\n"
    ofile.write(message)
ofile.close()

invert a matrix by Gaussian elimination - requires diagionally dominant system

[4.0, 1.5, 0.7, 1.2, 0.5] [1.0, 0, 0, 0, 0]
[1.0, 6.0, 0.9, 1.4, 0.7] [0, 1.0, 0, 0, 0]
[0.5, 1.0, 3.9, 3.2, 0.9] [0, 0, 1.0, 0, 0]
[0.2, 2.0, 0.2, 7.5, 1.9] [0, 0, 0, 1.0, 0]
[1.7, 0.9, 1.2, 2.3, 4.9] [0, 0, 0, 0, 1.0]
-----------------------------
[      A-Matrix          ]|[       A-Inverse        ]
_____________________________________________________
[4.0, 1.5, 0.7, 1.2, 0.5] | [0.27196423630168165, -0.05581183146290884, -0.032853102922602934, -0.016869919448735553, -0.0072026931722172435]
[1.0, 6.0, 0.9, 1.4, 0.7] | [-0.036786468827077756, 0.18691841183385363, -0.032062455842026744, -0.011456196435011407, -0.012617687833839365]
[0.5, 1.0, 3.9, 3.2, 0.9] | [-0.025949127789423248, -0.0013334022990376664, 0.26826513178341493, -0.10875073215127727, -0.004266180002777282]
[0.2, 2.0, 0.2, 7.5, 1.9] | [0.027047195749338872, -0.05063248905238324, 0.01649816113355711, 0.1486518640705042, -0.05619749842697155]
[1.7, 0.9, 1.2, 2.3, 4.9] | [-0.0939389748254409, 0.009124153146082323, -0.05615458031041434, -0.03518550386250331, 0.23632125710787594]
_____________________________________________________

Yay it worked. In practice we will not code our own inversion scripts, but will use numpy, however we now have a rudimentary script if we need it. How could we test if we indeed have an inverse?

Note

We could check our work using an on-line solver. And systematically solving the system 5 times with different RHS. Not too hard, but a bit of a pain - gets worse as our problem size grows! Here’s a useable solver website https://www.handymath.com/cgi-bin/matrix5.cgi

Solving Linear Systems (Optional)

Note

This optional section is presented as an introduction to algorithms/recipes for linear systems of equations. The method here is so-so computationally, but it does implement partial pivoting (so diagonal dominance is not vital), and finite precision artithmetic will work OK. In practice other methods would likely be more useful. A good source of information is Numerical Recipies

gaussian-elimination

pivoting

# linearsolver with pivoting adapted from 
# https://stackoverflow.com/questions/31957096/gaussian-elimination-with-pivoting-in-python/31959226
def linearsolver(A,b):
    n = len(A)
    M = A # this is equivalence A and M are destroyed during the solution!
    i = 0
    for x in M:
     x.append(b[i])
     i += 1
# row reduction with pivots
    for k in range(n):
     for i in range(k,n):
       if abs(M[i][k]) > abs(M[k][k]):
          M[k], M[i] = M[i],M[k]
       else:
          pass

     for j in range(k+1,n):
         q = float(M[j][k]) / M[k][k]
         for m in range(k, n+1):
            M[j][m] -=  q * M[k][m]
# allocate space for result
    x = [0 for i in range(n)]
# back-substitution
    x[n-1] =float(M[n-1][n])/M[n-1][n-1]
    for i in range (n-1,-1,-1):
      z = 0
      for j in range(i+1,n):
          z = z  + float(M[i][j])*x[j]
      x[i] = float(M[i][n] - z)/M[i][i]
# return result
    return(x)
#######

# Code to read A and b
amatrix = [] # null list to store matrix read
bvector = [] # null list to store vector read
rowNumA = 0
colNumA = 0
rowNumB = 0
afile = open("A.txt","r") # connect and read file for MATRIX A
for line in afile:
    amatrix.append([float(n) for n in line.strip().split()])
    rowNumA += 1
afile.close() # Disconnect the file
colNumA = len(amatrix[0])
afile = open("B.txt","r") # connect and read file for VECTOR b
for line in afile:
    bvector.append(float(line))  # vector read different -- just float the line
    rowNumB += 1
afile.close() # Disconnect the file

# check the arrays
if rowNumA != rowNumB:
    print ("row ranks not same -- aborting now")
    quit()
else:
    print ("row ranks same -- solve for x in Ax=b \n")
# print all columns each row
cmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
dmatrix = [[0 for j in range(colNumA)]for i in range(rowNumA)]
xvector = [0 for i in range(rowNumA)]
dvector = [0 for i in range(rowNumA)]

# copy amatrix into cmatrix to preserve original structure
cmatrix = [[amatrix[i][j] for j in range(colNumA)]for i in range(rowNumA)]
dmatrix = [[amatrix[i][j] for j in range(colNumA)]for i in range(rowNumA)]
dvector = [bvector[i] for i in range(rowNumA)]

dvector = linearsolver(amatrix,bvector) #Solve the linear system

print ("[A]*[x] = b \n")
for i in range(0,rowNumA,1):
    print ( (cmatrix[i][0:colNumA]), "* [","%9.5f"% (dvector[i]),"] = ", "%9.5f"% (bvector[i]))
#print ("-----------------------------")
#for i in range(0,rowNumA,1):
#    print ("%6.3f"% (dvector[i]))
#print ("-----------------------------")

row ranks same -- solve for x in Ax=b 

[A]*[x] = b 

[4.0, 1.5, 0.7, 1.2, 0.5] * [   0.15923 ] =    1.00000
[1.0, 6.0, 0.9, 1.4, 0.7] * [   0.09400 ] =    1.00000
[0.5, 1.0, 3.9, 3.2, 0.9] * [   0.12797 ] =    1.00000
[0.2, 2.0, 0.2, 7.5, 1.9] * [   0.08537 ] =    1.00000
[1.7, 0.9, 1.2, 2.3, 4.9] * [   0.06017 ] =    1.00000

Note

If we compare this result to an online solver with the same problem:

Here is the input

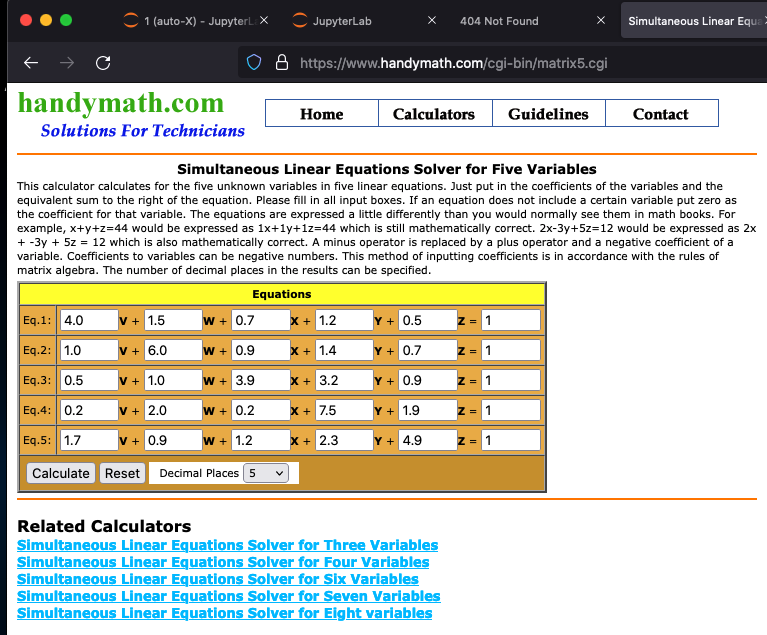
Here is the output

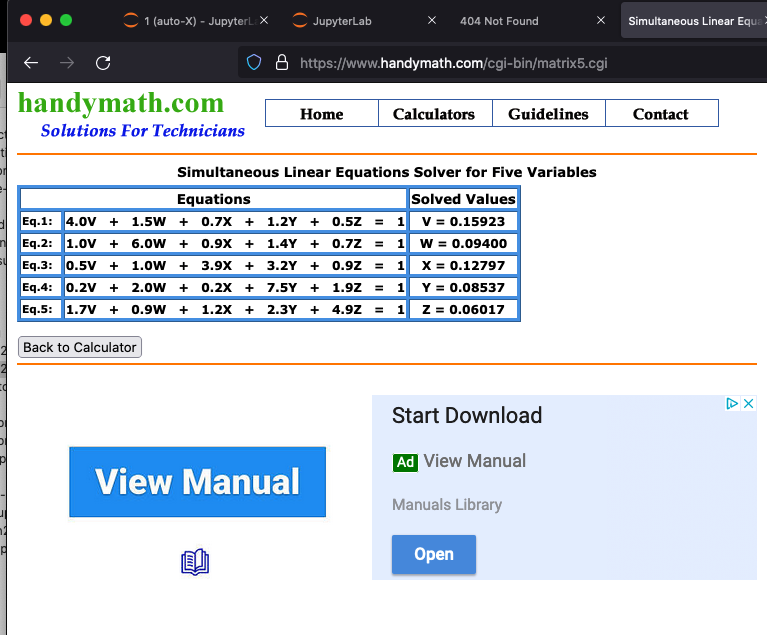
The result is the same as ours!

Future versions – applied examples ?

References

  1. Learn Python in One Day and Learn It Well. Python for Beginners with Hands-on Project. (Learn Coding Fast with Hands-On Project Book – Kindle Edition by LCF Publishing (Author), Jamie Chan https://www.amazon.com/Python-2nd-Beginners-Hands-Project-ebook/dp/B071Z2Q6TQ/ref=sr_1_3?dchild=1&keywords=learn+python+in+a+day&qid=1611108340&sr=8-3

  1. Matrix manipulation using numpy https://www.geeksforgeeks.org/matrix-manipulation-python/

  2. Outer products https://math.stackexchange.com/questions/973559/outer-product-of-two-matrices

  3. Inner products https://mathworld.wolfram.com/InnerProduct.html

  4. Gaussian-elimination (wikipedia)

  5. Pivoting (wikipedia)

  6. Numerical Recipies (website)

  7. Linearsolver with pivoting (code) slightly modded in this lesson.

Laboratory 8

Examine (click) Laboratory 8 as a webpage at Laboratory 8.html

Download (right-click, save target as …) Laboratory 8 as a jupyterlab notebook from Laboratory 8.ipynb

Exercise Set 8

Examine (click) Exercise Set 8 as a webpage at Exercise 8.html

Download (right-click, save target as …) Exercise Set 8 as a jupyterlab notebook at Exercise Set 8.ipynb