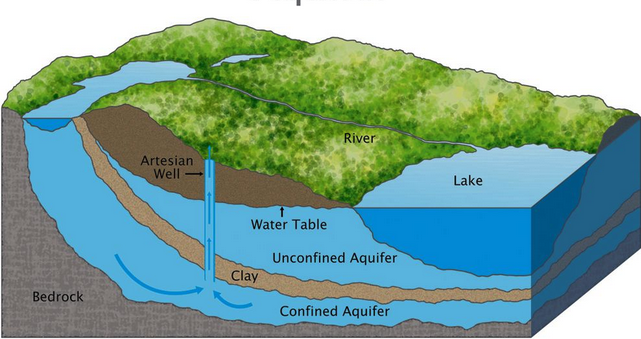
Groundwater Flow to Wells - I (pp. 156-162)¶
Terminology¶
Drawdown
Cone of Depression
Well interference
Have already examined steady flow solutions.
Unsteady Flow Solutions¶
There are two ways to proceede - just apply the groundwater flow equatrions or use a plasuibility argument to infer what solutions might look like.
Infer Structure










Apply Groundwater Flow Equations


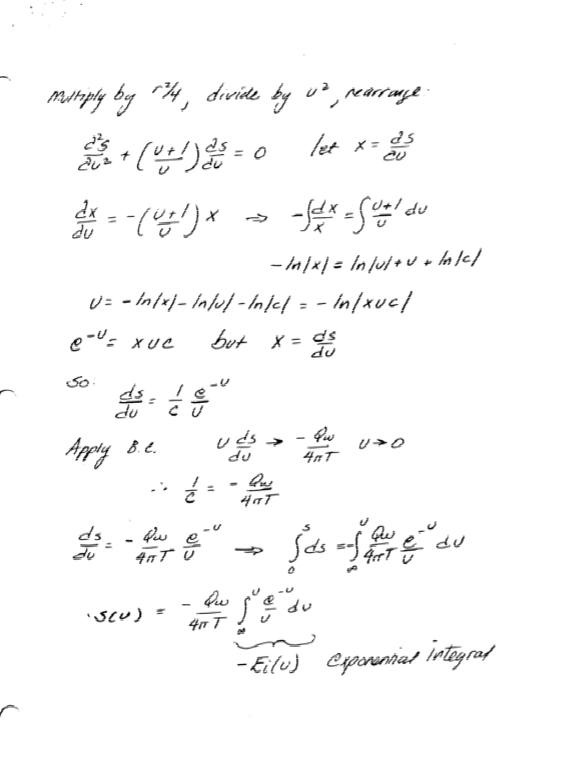



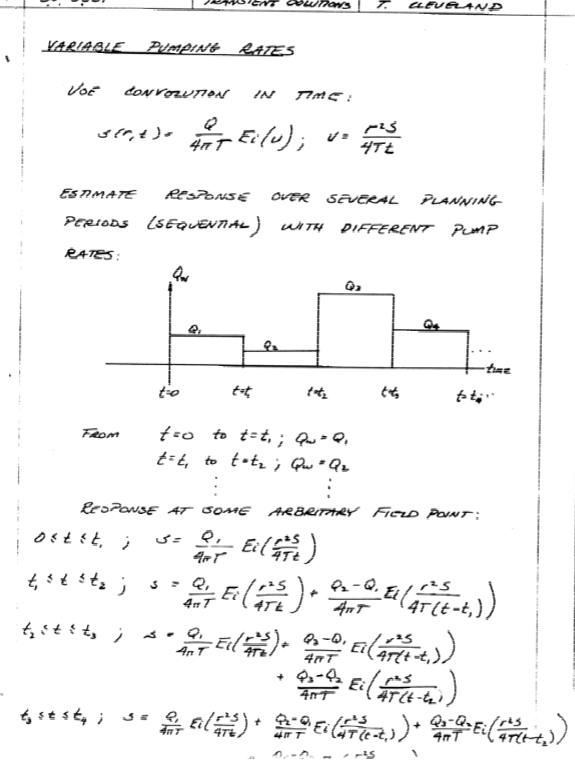
Implementing Solutions¶
In the olden days, one would look up well function values in tabulations such as TWRI BOOK 3 Chapter B3 TYPE CURVES FOR SELECTED PROBLEMS OF FLOW TO WELLS IN CONFINED AQUIFERS
Many of the special functions were leter embedded in the analysis packages for spreadsheets.
Or one can simply program themselves as shown below:
def W(u): # Theis well function using exponential integral
import scipy.special as sc
w = sc.expn(1,u)
return(w)
def s(radius,time,storage,transmissivity,discharge): # Drawdown function using exponential integral
import math
u = ((radius**2)*(storage))/(4*transmissivity*time)
s = ((discharge)/(4*math.pi*transmissivity))*W(u)
return(s)
Lets choose an the example from the book on pg. 162 to illustrate the homebrew script. The relevant problem parametrs are:
\(K = 14.9 m/d\)
\(b = 20.1 m\)
\(T = Kb = 299 m^2/d\)
\(S = 0.0051\)
\(Q_w = 2725 m^3/d\)
\(r = 7.0 m \)
\(t = 1 d\)
radius=7.0
time=1.0
storage=0.0051
transmissivity=299
discharge=2725
print("Drawdown is ",round(s(radius,time,storage,transmissivity,discharge),2)," meters")
Drawdown is 5.73 meters