Groundwater Models¶

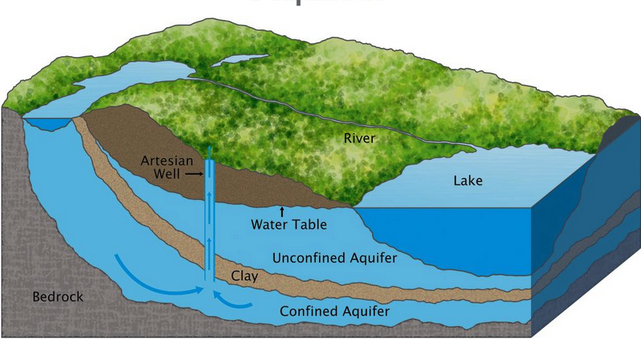
Flow in porous media is a topic that appears in many branches of engineering and science, e.g., ground water hydrology, reservoir engineering, soil science, soil mechanics, and chemical engineering (filtration). The aquifer, which is the porous medium domain of the hydrologist, or the oil reservoir, which is the porous medium of the petroleum engineer are typical examples. Fig. 14 is a sketch of different aquifer classifications.

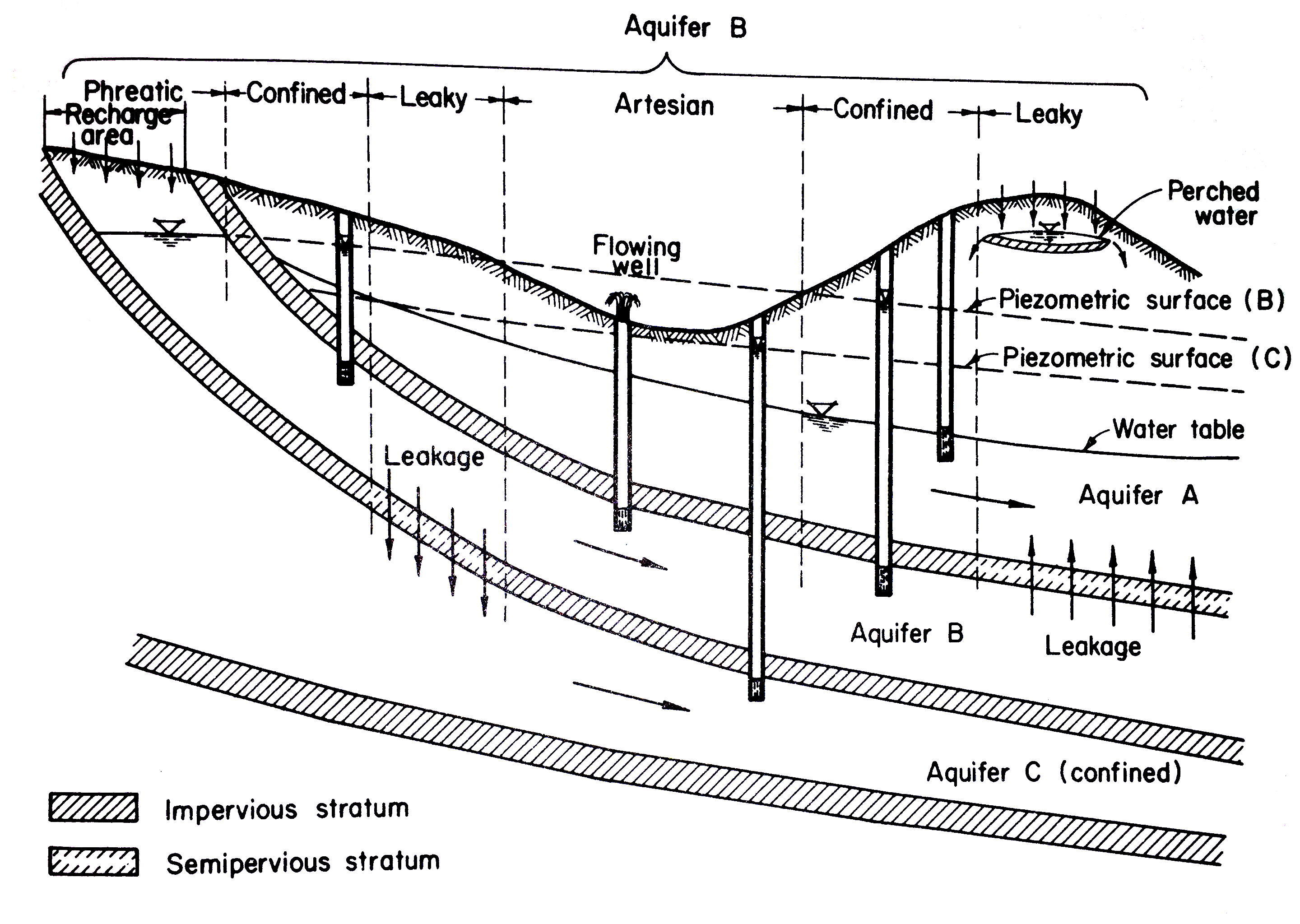
Fig. 14 Aquifer Schematic¶

A confined aquifer (pressure aquifer) is one bounded above and below by impermeable formations. In a well penetrating such an aquifer, the water level will rise above the base of the confining formation. Water levels in wells that sample a certain aquifer define an imaginary surface called the piezometric surface.

An unconfined aquifer (water table aquifer; phreatic aquifer) is one with the water table as its upper boundary. The classifications are important because the equations of motion are different in different kinds of aquifers.

Storativity¶

Storativity of an aquifer is the relationship between changes in head within the aquifer and the quantity of water stored in the aquifer. The dominant mechanism of storage is different for confined and unconfined aquifers. Fig. 15 is a sketch depicting the storage process in a confined, and an unconfined aquifer.

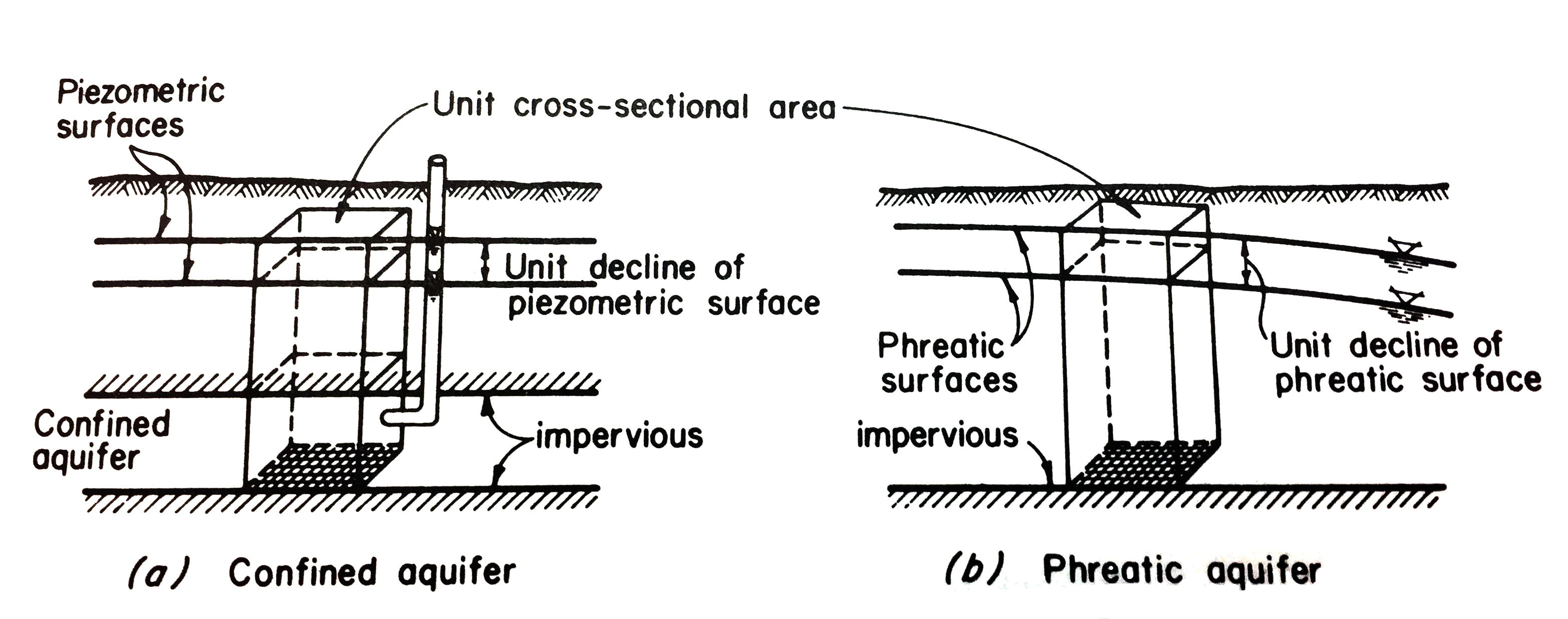
Fig. 15 Storage Mechanisms¶

In a confined aquifer the water is stored or released by compression and decompression of water and the solid matrix (like a sponge squeezed while wrapped in plastic wrap). In an unconfined aquifer the water is stored or released from the pore space when the water table elevation changes.

The storage coefficient (confined) or specific yield (unconfined) is the volume of water added to (or removed from) storage per unit area of aquifer per unit change in head. The usual symbols are \(S\), and \(S_y\).

Permeability¶

Permeability is the material property that relates the resistance of flow through the porous medium to the hydraulic gradient.

Head Loss Models¶

Darcy’s law (a linear flux model) is the head loss model used for porous media flow.

Darcy’s law is usually presented as a discharge model

\[Q = -KA\frac{\Delta h}{\Delta x}\]

Expressed as a head loss model it is rearranged as

\[ h_L = \frac{QL}{KA} \]

where \(Q\) is the discharge in the aquifer, \(L\) is the length in the flow direction, \(A\) is the cross sectional area of aquifer (pore space and solid phase), \(K\) is the hydraulic conductivity (sometimes called the permeability).

A more useful (for computation) form of the head loss model, is to express it (the loss equation) as an equation of motion as in

\[Q = -KA\frac{\partial h}{\partial x}\]

where \(- \frac{\partial h}{\partial x}\) is the hydraulic gradient (slope of the hydraulic grade line) in the aquifer.

Fig. 16 is a diagram that illustrates the relationships expressed by Darcy’s law.

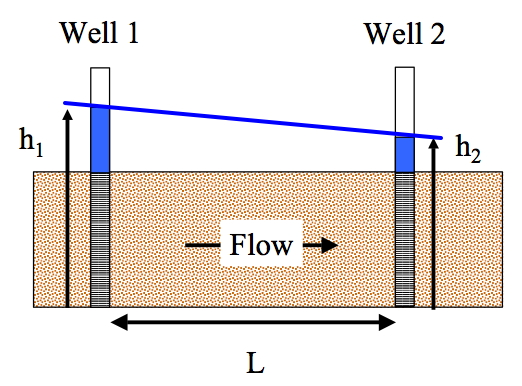
Fig. 16 Schematic diagram of unidirectional flow in a generic aquifer, showing heads in two measuring wells located distance \(L\) apart¶

The cross-sectional flow area, \(A\), is the product of height of the aquifer block and its width (in this case the width is into the plane of the paper).
The distance between two measurement points is \(L\). The head at the two points is \(h_1\) and \(h_2\).
The gradient of head, \(\frac{\partial h}{\partial x}\), is \(\frac{h_2 - h_1}{L}\).
The hydraulic gradient is \(- \frac{\partial h}{\partial x}\), is \(\frac{h_1 - h_2}{L}\).

Finally Darcy’s law (for the drawing) is \(Q = K A \frac{h_1 - h_2}{L}\).

Equilibrium Models¶

Equilibrium models imply that the head distribution is constant in time.

Note

Steady-state is a common, thermodynamically incorrect way to refer to an equilibrium model. Keep in mind, flow is non zero, hence the flow is steady, but the thermodynamic state of the system is not. It’s an almost trivial point - but relevant when the model is used for geochemistry explaination.

Confined Aquifer Flow Modeling Theory¶

Using Figure Fig. 16 as a starting point, one can develop a computational model of flow in a confined aquifer. Let’s decide that the distance \(L\) in the figure is going to be divided into a series of connected, small blocks. The flow direction in the figure will be declared the \(x\) direction, the depth into the drawing is declared the \(y\) direction, and the height of the block is declared the \(z\) direction.

Fig. 17 is a diagram of one such small block.

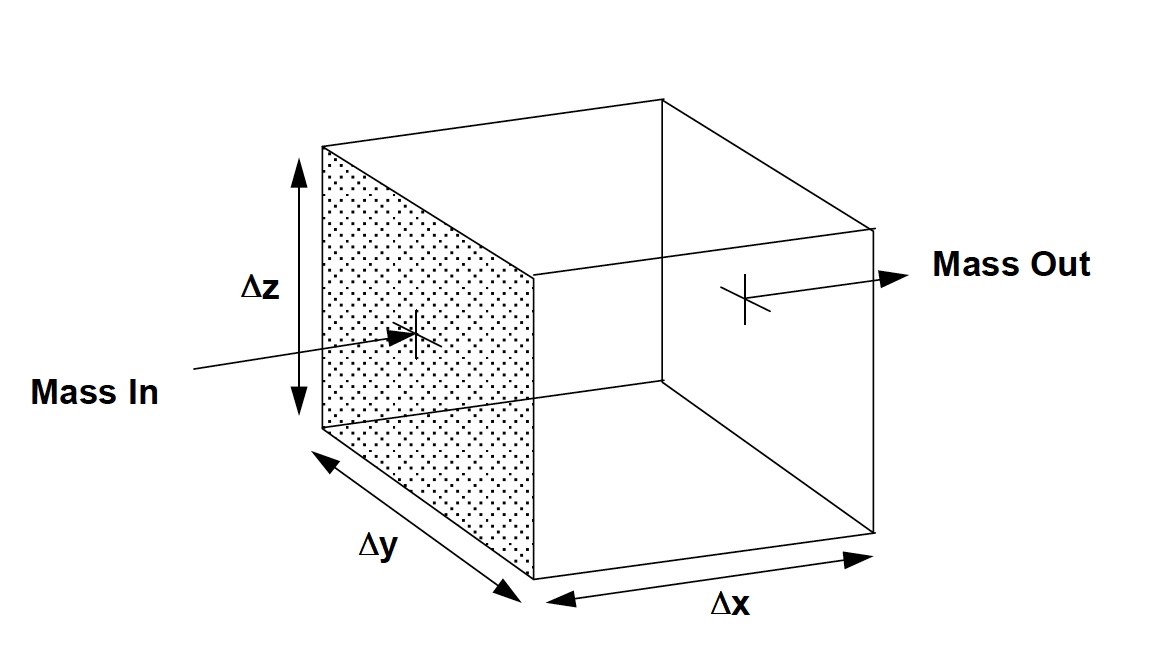
../../_images/single-computational-cell.png

Fig. 17 Single computational cell definition sketch¶

Using this diagram we can now develop a set of expressions for the cell volume, solids volume in the cell, pore volume in the cell (where water actually can flow), and solids mass.

First some definitional expressions for each cell:

Cell Volume: \(V_{cell} = \Delta x \times \Delta y \times \Delta z\)

Solids Volume: \(V_{solid} =(1-\omega) \Delta x \times \Delta y \times \Delta z\)

Void (Pore) Volume: \(V_{pore} = \omega \Delta x \times \Delta y \times \Delta z\)

Solids Mass: \(M_{solid} = \rho_{s} (1-\omega) \Delta x \times \Delta y \times \Delta z\)

Next write a mass balance for water in the cell;

\[ \frac{d M_{water}}{dt} = M_{Inflow} - M_{Outlfow} \]

The left side of the expression is simply the storage term, and in the context of storage coefficients and aquifer head is replaced by

\[ {\frac{d M_{water}}{dt}\mid}_{cell} =\rho_{w} S_{s} \Delta x \Delta y \Delta z \frac{\partial h_i}{\partial t} \]

where \(h_i\) is the head in the \(i-\)th cell.

The right hand side of the expression is based on writing Darcy’s law for the cell, and using values in adjacent (hydraulically connected) cells.

Fig. 18 is a diagram of three such connected blocks.

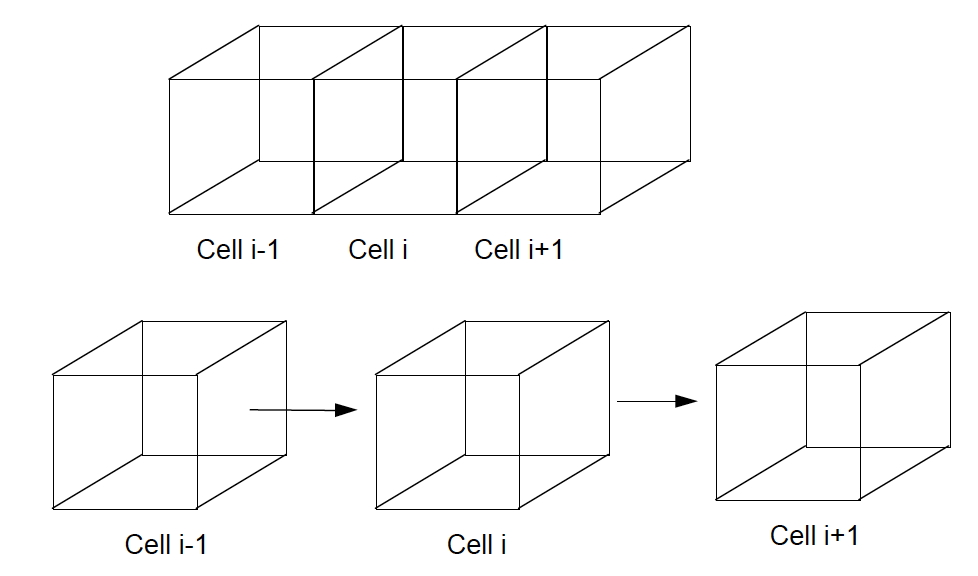
../../_images/multiple-computational-cell.png

Fig. 18 Multiple computational cell definition sketch¶

The \(i-\)th cell is the cell of interest, the cell to the left is cell ID \(i-1\), and the cell to the right is cell ID \(i+1\).

We now write Darcy’s law for each face of cell \(i\), treating the head in each of the cell centers as if they were the sampling wells of Fig. 16 (In the context of Fig. 16, the cell face is halfway between the two wells; the cell centers are at the wells.)

Darcy’s law for the left face is

\[ M_{Inflow} = Q_{left} =\rho_{w} K \Delta y \Delta z \frac{h_{i-1} - h_{i}}{\Delta x} \]

Similarly for the right face,

\[ M_{Outflow} = Q_{right} =\rho_{w} K \Delta y \Delta z \frac{h_{i} - h_{i+1}}{\Delta x} \]

Now combine these together in the mass balance

\[ \rho_{w} S_{s} \Delta x \Delta y \Delta z \frac{\partial h_i}{\partial t} = (\rho_{w} K \Delta y \Delta z \frac{h_{i-1} - h_{i}}{\Delta x}) - (\rho_{w} K \Delta y \Delta z \frac{h_{i} - h_{i+1}}{\Delta x}) \]

Next divide by the water density \(\rho_{w}\),

\[ S_{s} \Delta x \Delta y \Delta z \frac{\partial h_i}{\partial t} = (K \Delta y \Delta z \frac{h_{i-1} - h_{i}}{\Delta x}) - (K \Delta y \Delta z \frac{h_{i} - h_{i+1}}{\Delta x}) \]

Then divide by cell width \(\Delta y \),

\[ S_{s} \Delta x \Delta z \frac{\partial h_i}{\partial t} = (K \Delta z \frac{h_{i-1} - h_{i}}{\Delta x}) - (K \Delta z \frac{h_{i} - h_{i+1}}{\Delta x}) \]

Rewrite the right hand side into gradient of head form

\[ S_{s} \Delta x \Delta z \frac{\partial h_i}{\partial t} = (K \Delta z \frac{h_{i+1} - h_{i}}{\Delta x}) - (K \Delta z \frac{h_{i} - h_{i-1}}{\Delta x}) = {K \Delta z \frac{\partial h}{\partial x}}\mid_{i~\rightarrow i+1} - {K \Delta z \frac{\partial h}{\partial x}}\mid_{i-1~\rightarrow i} \]

Divide by cell distance, \(\Delta x\),

\[ S_{s} \Delta z \frac{\partial h_i}{\partial t} = \frac{{K \Delta z \frac{\partial h}{\partial x}}\mid_{i~\rightarrow i+1} - {K \Delta z\frac{\partial h}{\partial x}}\mid_{i-1~\rightarrow i}}{\Delta x} \]

Take limit as \(\Delta x~\rightarrow0\),

\[ S_{s} \Delta z \frac{\partial h}{\partial t} = \frac{\partial}{\partial x}({K \Delta z \frac{\partial h}{\partial x}}) \]

Finally, stipulate that \(S_{s} \Delta z = S\), the storage coefficient (for confined aquifer), and define the aquifer transmissivity as \(K \Delta z = T\) and we have performed a nicely back-handed way to get the partial differential equation of aquifer flow.

\[ S \frac{\partial h}{\partial t} = \frac{\partial}{\partial x}({T \frac{\partial h}{\partial x}}) \]

Solution Methods¶

Ironically, the analysis actually provides an algorithm to approximate head in the aquifer

Finite-Difference Methods – 1 Spatial Dimension¶

Here we will use the equation obtained after dividing by the water density as a starting point for simulating aquifer behavior.

As a first model, lets consider the steady flow situation, in which case the left hand side vanishes (there is no change in storage).

\[ 0 = (K \Delta y \Delta z \frac{h_{i-1} - h_{i}}{\Delta x}) - (K \Delta y \Delta z \frac{h_{i} - h_{i+1}}{\Delta x}) \]

Next we will use the arithmetic mean values of the material properties (\(K\)) at the cell interfaces, so the difference equation becomes

Note

Other spatial averaging formulas are employed, but the arithmetic mean is quite common

\[ 0 = (\frac{1}{2}(K_{i-1}+K_{i}) \Delta y \Delta z \frac{h_{i-1} - h_{i}}{\Delta x}) - (\frac{1}{2}(K_{i}+K_{i-1}) \Delta y \Delta z \frac{h_{i} - h_{i+1}}{\Delta x}) \]

Now lets group some constants:

\[\begin{split} \begin{matrix} A_{i} = \frac{1}{2 \Delta x}(K_{i-1}+K_{i}) \Delta y \Delta z \\ B_{i} = \frac{1}{2 \Delta x}(K_{i}+K_{i+1}) \Delta y \Delta z \end{matrix} \end{split}\]

Now substitute into the difference equation

\[ 0 = A_{i}(h_{i-1}) -(A_{i}+B_{i})(h_{i}) + B_{i}(h_{i+1}) \]

Now all that remains is to specify boundary conditions, and then implement an algorithm to solve the resulting system of algebraic equations.

Note

I have assumed that the spatial step, \(\Delta x\) is the same for each cell – it doesn’t have to be, but relaxing that assumption complicates the specifications of the constants \(A\) and \(B\).

Some of the plausible boundary conditions are:

Specified head boundary (pretty easy to specify in a computer representation).
Zero-flux boundary (also easy to specify using the cell-centered formulation herein).
Specified flux boundary (using a modeling trick not too hard to specify).

These three types of conditions should handle the majority of practical situations where one would need to model an aquifer system.

Lets examine the difference equation a little bit – assume we have the correct values then

\[ h_{i} = \frac{A_{i}(h_{i-1}) + B_{i}(h_{i+1})}{(A_{i}+B_{i})} \]

which suggests a nice algorithm.

We will simply apply boundary conditions, then evaluate the expression for each cell, and after we compute the expression for all the cells, we will repeat the process until the solution stops changing.

Computationally, we are employing a Jacobi iteration scheme, which will work nicely for this particular problem structure.
An alternative, equally valid, would be to construct the linear system of equations (in this case it will be a three-banded matrix), and apply an appropriate row reduction technique to find the solution.

The example 1D applications are presented below as special cases of 2D models.

Finite-Difference Methods – 2 Spatial Dimensions¶

If we perform an analysis in the same way as we did to arrive at

\[ S \frac{\partial h}{\partial t} = \frac{\partial}{\partial x}({T \frac{\partial h}{\partial x}}) \]

except now include another direction (the y-direction) we will have an aquifer in two spatial dimensions. The governing equation becomes

\[ S \frac{\partial h}{\partial t} = \frac{\partial}{\partial x}({T_x \frac{\partial h}{\partial x}}) + \frac{\partial}{\partial y}({T_y \frac{\partial h}{\partial y}}) \]

The meanings of the terms are the same, except the transmissivity terms now have subscripts to indicate they can have different values depending on direction

Then as before we will construct the difference-equation model from a multiple-cell balance model of the aquifer at a cell of interest, then extend the equations to cover the entire model domain.

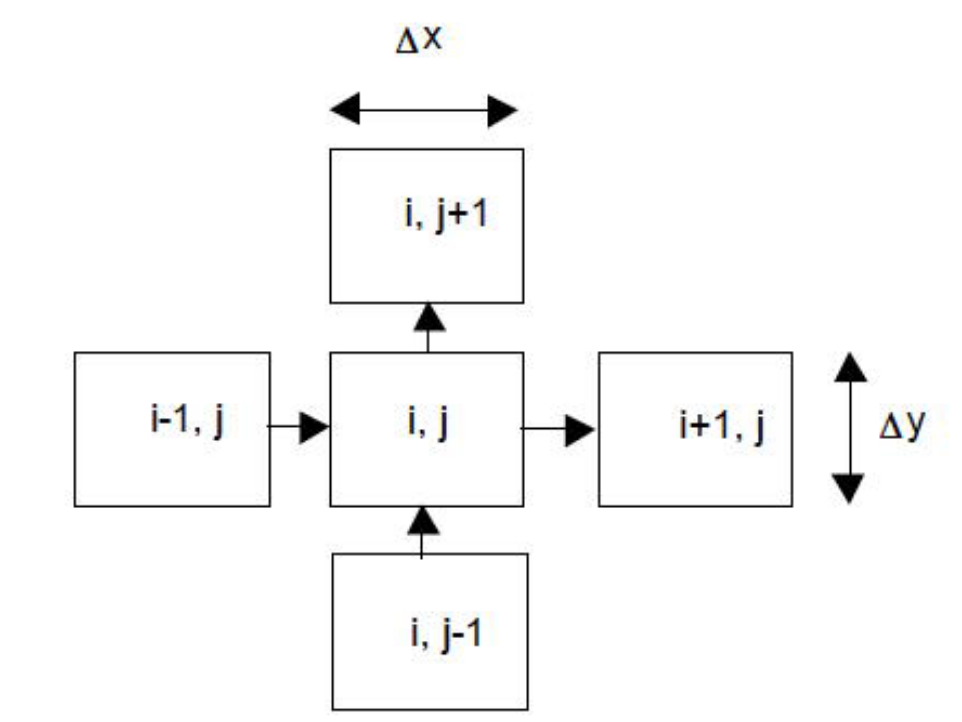
Fig. 19 Plan view schematic of 2-dimensional multiple cell balance computational stencil.¶

Fig. 19 is a plan view schematic of a aquifer with flow to be computed in two directions (x and y). The cell indexing convention in the sketch is that rows are in- dexed by the letter j and columns are indexed by the letter i. This naming convention is arbitrary; in some instances it may be preferable to reverse the convention. The schematic also shows the assumed flow directions; for column i, flows are upward in the drawing, and for row j, flows are from left to right. If indeed the opposite is true for a given set of boundary conditions and material properties, then the flows will be computed as negative numbers – hence the convention here is that “positive flow” is right and up.

As in the one-dimensional development the storage term is

\[ \frac{dM_{water}}{dt}\mid_cell = \rho_w S_s \Delta x \Delta y \Delta z \frac{\partial h_{i,j}}{\partial t} (218) \]

where \(h_{i,j}\) is the head in the (i−th, j−th) cell.

The mass flows entering the (i−th, j−th) cell are:

\[ M_{Inflow} = Q_{left} + Q_{bottom} = \rho_w K_x\Delta y\Delta z \frac{h_{i−1,j} − h_{i,j}}{∆x} + \rho_w K_y \Delta x \Delta z \frac{h_{i,j−1} − h_{i,j}}{\Delta y} \]

The mass flows leaving the (i − th, j − th} cell are:

\[ M_{Outflow} = Q_{right} + Q_{top} = \rho_w K_x\Delta y\Delta z \frac{h_{i,j} − h_{i+1,j}}{\Delta x} + \rho_w K_y \Delta x \Delta z \frac{h_{i,j} − h_{i,j+1}}{\Delta y} \]

Now write the entire balance equation

\[ \rho_w S_s \Delta x \Delta y \Delta z \frac{\partial h_{i,j}}{\partial t}= [\rho_w K_x\Delta y\Delta z \frac{h_{i−1,j} − h_{i,j}}{∆x} + \rho_w K_y \Delta x \Delta z \frac{h_{i,j−1} − h_{i,j}}{\Delta y}]−[\rho_w K_x\Delta y\Delta z \frac{h_{i,j} − h_{i+1,j}}{\Delta x} + \rho_w K_y \Delta x \Delta z \frac{h_{i,j} − h_{i,j+1}}{\Delta y} ] \]

Next replace \(S_s \Delta z\) with the storage coefficient \(S\), and the \(K_{x,y}\Delta z\) with the transmissivity T_{x,y} terms, and divide by the density of the fluid and the cell plan view area \(\Delta x \Delta y\) to obtain a more compact form of the difference equation.

\[ S \frac{\partial h_{i,j}}{\partial t} = [ \frac{1}{\Delta x} T_x \frac{h_{i−1,j} − h_{i,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j-1} − h_{i,j}}{\Delta y}]-[\frac{1}{\Delta x} T_x \frac{h_{i,j} − h_{i+1,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j} − h_{i,j+1}}{\Delta y}] \]

As in the one-dimensional case, lets again consider steady flow (we will do transient flows later on)

\[ 0 = [ \frac{1}{\Delta x} T_x \frac{h_{i−1,j} − h_{i,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j-1} − h_{i,j}}{\Delta y}]-[\frac{1}{\Delta x} T_x \frac{h_{i,j} − h_{i+1,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j} − h_{i,j+1}}{\Delta y}] \]

Also as in the one-dimensional case, we will approximate the spatial variation of the material properties (transmissivity) as arithmetic mean values between two cells, so making the following definitions:

\[\begin{split} A_{i,j} = \frac{1}{2∆x^2} (T_{x,(i−1,j)} + T_{x,(i,j)})\\ B_{i,j} = \frac{1}{2∆x^2} (T_{x,(i,j)} + T_{x,(i+1,j)})\\ C_{i,j} = \frac{1}{2∆y^2} (T_{y,(i,j−1)} + T_{y,(i,j)})\\ D_{i,j} = \frac{1}{2∆y^2} (T_{y,(i,j)} + T_{y,(i,j+1)})\\ \end{split}\]

Substitution into the difference equation yields

\[ 0 = A_{i,j} h_{i−1,j} + B_{i,j} h_{i+1,j} − (A_{i,j} + B_{i,j} + C_{i,j} + D_{i,j} )h_{i,j} + C_{i,j} h_{i,j−1} + D_{i,j} h_{i,j+1} \]

As before we can explicitly write the cell equation for hi,j as

\[ h_{i,j} = \frac{A_{i,j} h_{i−1,j} + B_{i,j} h_{i+1,j} + C_{i,j} h_{i,j−1} + D_{i,j} h_{i,j+1}}{A_{i,j} + B_{i,j} + C_{i,j} + D_{i,j} } \]

This difference equation represents an approximation to the governing flow equation, the accuracy depending on the cell size. Boundary conditions are applied directly into the analogs (another name for the difference equations) at appropriate locations on the computational grid. Also as in the one-dimensional case we can generate solutions either by iteration or solving the resulting linear system.

Homebrew - Example 1¶

2D Steady Flow in a Confined Aquifer using Jacobi Iteration We will start the example with a simple physical condition and use Jacobi iteration to obtain a solution. We will also incorporate two kinds of boundary conditions (fixed head, and no-flow boundaries).

Note

Jacobi iteration for large domain problems (say 200x200) or bigger, is pretty inefficient – better iterative methods are available; however they simply represent clever changes to the basic iteration methods explained here, hence Jacobi is a good place to start, and is incredibly easy to program.

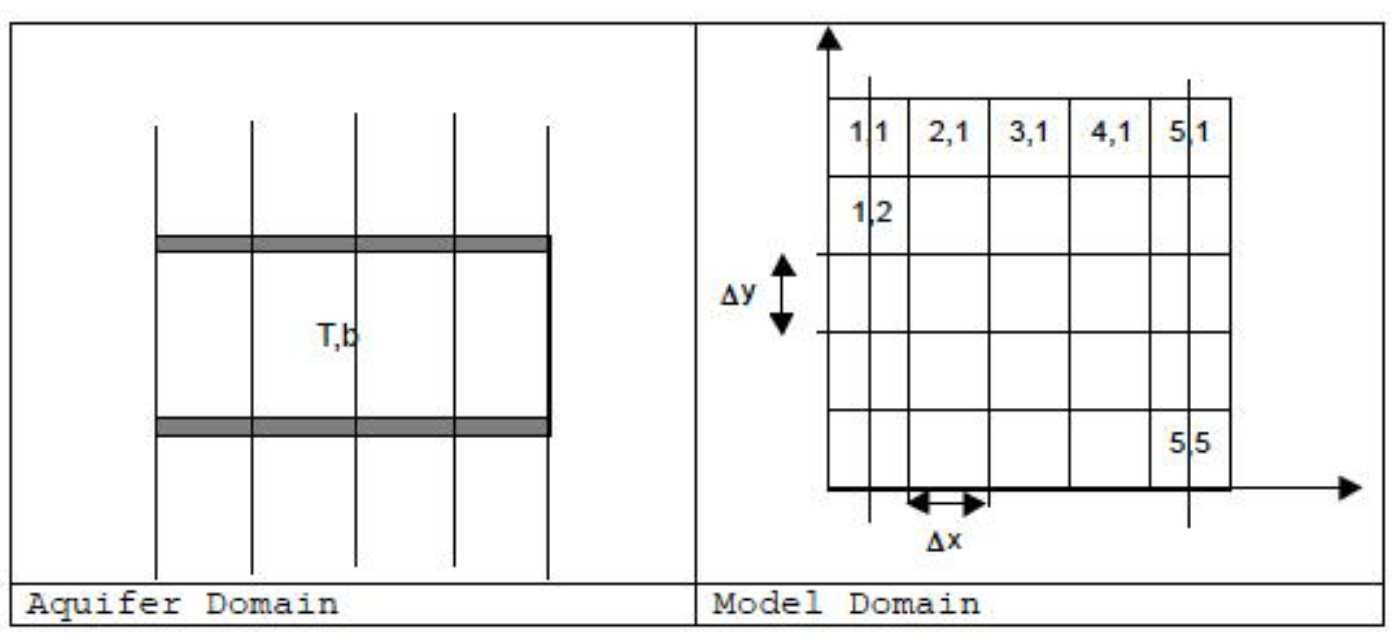
Fig. 20 Plan view schematic of 2-dimensional multiple cell balance computational stencil.¶

Fig. 20 is a schematic of this example. The right panel of the figure shows the index naming convention. The known material properties are transmissivity (in each direction, at each cell center, and the thickness of the aquifer (b == ∆z). Our task is to simulate the aquifer with the 5 x 5 model shown. The left and right boundaries will be treated as specified head boundaries. The upper and lower boundary will be treated as no flow boundaries. The head on the left is 100 meters and the right is 60 meters (same as before). The transmissivity (\(K_{x,y}\Delta z=10\)) square meters per second for this exampls suppose \(K = 0.2\) meters per second, and \(\Delta z = 50\) meters. The spatial dimensions are \(\Delta x = 100\) meters and \(\Delta y = 100\) meters

The listing below implements the method – in this case there are data read/write methods (to read and build matrices), and notice how the no-flow boundary conditions are implemented.

The data are stored in an input file to generalize the script

input1.txt contents:

100
100
50
5
5
1e-4
100
200 300 400 500
200 300 400 500
100 100 100 60
100 100 100 60
100 100 100 60
100 100 100 60
100 100 100 60
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2
2 0.2 0.2 0.2 0.2

def sse(matrix1,matrix2):
    sse=0.0
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            sse=sse+(matrix1[ir][jc]-matrix2[ir][jc])**2
    return(sse)

def update(matrix1,matrix2):
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            matrix2[ir][jc]=matrix1[ir][jc]
    return(matrix2)

def writearray(matrix):
    nr=len(matrix) # get row count
    nc=len(matrix[0]) # get column count
    import numpy as np
    new_list = list(np.around(np.array(matrix), 1))    
    for ir in range(nr):
        print(ir,new_list[ir][:])
    return()

localfile = open("input1.txt","r") # connect and read file for 2D gw model
deltax = float(localfile.readline())
deltay = float(localfile.readline())
deltaz = float(localfile.readline())
nrows = int(localfile.readline())
ncols = int(localfile.readline())
tolerance = float(localfile.readline())
maxiter = int(localfile.readline())
distancex = [] # empty list
distancex.append([float(n) for n in localfile.readline().strip().split()])
distancey = [] # empty list
distancey.append([float(n) for n in localfile.readline().strip().split()])
head =[] # empty list
for irow in range(nrows):
        head.append([float(n) for n in localfile.readline().strip().split()])
hydcondx = [] # empty list
for irow in range(nrows):
        hydcondx.append([float(n) for n in localfile.readline().strip().split()])
hydcondy = [] # empty list
for irow in range(nrows):
        hydcondy.append([float(n) for n in localfile.readline().strip().split()])
localfile.close() # Disconnect the file
##
amat = [[0 for j in range(ncols)] for i in range(nrows)]
bmat = [[0 for j in range(ncols)] for i in range(nrows)]
cmat = [[0 for j in range(ncols)] for i in range(nrows)]
dmat = [[0 for j in range(ncols)] for i in range(nrows)]
##
for irow in range(1,nrows-1):
    for jcol in range(1,ncols-1):
        amat[irow][jcol] = (( hydcondx[irow-1][jcol  ]+ hydcondx[irow  ][jcol  ]) * deltaz ) /(2.0*deltax**2)
        bmat[irow][jcol] = (( hydcondx[irow  ][jcol  ]+ hydcondx[irow+1][jcol  ]) * deltaz ) /(2.0*deltax**2)
        cmat[irow][jcol] = (( hydcondy[irow  ][jcol-1]+ hydcondy[irow  ][jcol  ]) * deltaz ) /(2.0*deltay**2)
        dmat[irow][jcol] = (( hydcondy[irow  ][jcol  ]+ hydcondy[irow  ][jcol+1]) * deltaz ) /(2.0*deltay**2)
##
headold = [[0 for jc in range(ncols)] for ir in range(nrows)] #force new matrix
headold = update(head,headold) # update
##writearray(head)
##print("----")
##writearray(headold)
##print("--------")
tolflag = False
for iter in range(maxiter):
##    print("begin iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
##    print("--------")
# first and last row special == no flow boundaries
    for jcol in range(ncols):
        head [0    ][jcol ] = head[1][jcol ]
        head [nrows-1][jcol ] = head[nrows-2][jcol ]
# interior updates
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            head[irow][jcol]=( amat[irow][jcol]*head[irow-1][jcol  ] 
                              +bmat[irow][jcol]*head[irow+1][jcol  ] 
                              +cmat[irow][jcol]*head[irow  ][jcol-1] 
                              +dmat[irow][jcol]*head[irow  ][jcol+1])/(amat[ irow][jcol ]+ bmat[ irow][jcol ]+ cmat[ irow][jcol ]+ dmat[ irow][jcol ])
# test for stopping iterations
##    print("end iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
    percentdiff = sse(head,headold)
    if  percentdiff <= tolerance:
        print("Exit iterations in velocity potential because tolerance met ")
        print("Iterations =" , iter+1 ) ;
        tolflag = True
        break
    headold = update(head,headold)
print("End Calculations")
print("Iterations    = ",iter+1)
print("Closure Error = ",round(percentdiff,3))
print("Head Map")
print("----")
writearray(head)
print("----")

Exit iterations in velocity potential because tolerance met 
Iterations = 31
End Calculations
Iterations    =  31
Closure Error =  0.0
Head Map
----

[100.  90.  80.  70.  60.]
[100.  90.  80.  70.  60.]
[100.  90.  80.  70.  60.]
[100.  90.  80.  70.  60.]
[100.  90.  80.  70.  60.]
----

Homebrew - Example 2¶

2D Vertical Slice in a Confined Aquifer using Jacobi Iteration with Low Permeability Inclusion Fig. 21 is a schematic of a different situation that now only requires us to change the contents of the data file, and re-run the scripts unchanged.

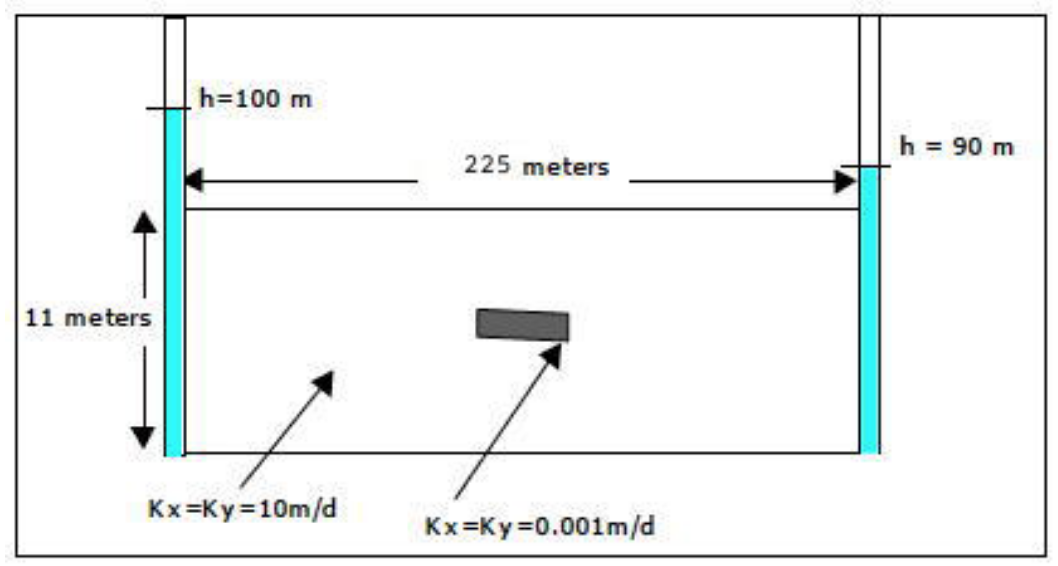
Fig. 21 Plan view schematic of 2-dimensional multiple cell balance computational stencil.¶

The input file is listed below. The boundary conditions are still directly coded into the algorithm, and that would be a useful modification to the code - general boundary condition information. Another useful addition is to generate graphical output, as the model size increases the output is harder to interpret - a contour map would be quite useful!

input2.txt contents

1
10
1
13
23
1e-9 
9000
15 25 35 45 55 65 75 85 95 105 115 125 135 145 155 165 175 185 195 205 215 225
5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10

def sse(matrix1,matrix2):
    sse=0.0
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            sse=sse+(matrix1[ir][jc]-matrix2[ir][jc])**2
    return(sse)

def update(matrix1,matrix2):
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    ##print(nr,nc)
    for ir in range(nr):
        for jc in range(nc):
            ##print(ir,jc)
            matrix2[ir][jc]=matrix1[ir][jc]
    return(matrix2)

def writearray(matrix):
    nr=len(matrix) # get row count
    nc=len(matrix[0]) # get column count
    import numpy as np
    new_list = list(np.around(np.array(matrix), 3))    
    for ir in range(nr):
        print(ir,new_list[ir][:])
    return()

localfile = open("input2.txt","r") # connect and read file for 2D gw model
deltax = float(localfile.readline())
deltay = float(localfile.readline())
deltaz = float(localfile.readline())
nrows = int(localfile.readline())
ncols = int(localfile.readline())
tolerance = float(localfile.readline())
maxiter = int(localfile.readline())
distancex = [] # empty list
distancex.append([float(n) for n in localfile.readline().strip().split()])
distancey = [] # empty list
distancey.append([float(n) for n in localfile.readline().strip().split()])
head =[] # empty list
for irow in range(nrows):
        head.append([float(n) for n in localfile.readline().strip().split()])
hydcondx = [] # empty list
for irow in range(nrows):
        hydcondx.append([float(n) for n in localfile.readline().strip().split()])
hydcondy = [] # empty list
for irow in range(nrows):
        hydcondy.append([float(n) for n in localfile.readline().strip().split()])
localfile.close() # Disconnect the file
##
amat = [[0 for j in range(ncols)] for i in range(nrows)]
bmat = [[0 for j in range(ncols)] for i in range(nrows)]
cmat = [[0 for j in range(ncols)] for i in range(nrows)]
dmat = [[0 for j in range(ncols)] for i in range(nrows)]
##
for irow in range(1,nrows-1):
    for jcol in range(1,ncols-1):
        amat[irow][jcol] = (( hydcondx[irow-1][jcol  ]+ hydcondx[irow  ][jcol  ]) * deltaz ) /(2.0*deltax**2)
        bmat[irow][jcol] = (( hydcondx[irow  ][jcol  ]+ hydcondx[irow+1][jcol  ]) * deltaz ) /(2.0*deltax**2)
        cmat[irow][jcol] = (( hydcondy[irow  ][jcol-1]+ hydcondy[irow  ][jcol  ]) * deltaz ) /(2.0*deltay**2)
        dmat[irow][jcol] = (( hydcondy[irow  ][jcol  ]+ hydcondy[irow  ][jcol+1]) * deltaz ) /(2.0*deltay**2)
##
headold = [[0 for jc in range(ncols)] for ir in range(nrows)] #force new matrix
headold = update(head,headold) # update
##writearray(head)
##print("----")
##writearray(headold)
##print("--------")
tolflag = False
for iter in range(maxiter):
##    print("begin iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
##    print("--------")
# first and last row special == no flow boundaries
    for jcol in range(ncols):
        head [0    ][jcol ] = head[1][jcol ]
        head [nrows-1][jcol ] = head[nrows-2][jcol ]
# interior updates
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            head[irow][jcol]=( amat[irow][jcol]*head[irow-1][jcol  ] 
                              +bmat[irow][jcol]*head[irow+1][jcol  ] 
                              +cmat[irow][jcol]*head[irow  ][jcol-1] 
                              +dmat[irow][jcol]*head[irow  ][jcol+1])/(amat[ irow][jcol ]+ bmat[ irow][jcol ]+ cmat[ irow][jcol ]+ dmat[ irow][jcol ])
# test for stopping iterations
##    print("end iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
    percentdiff = sse(head,headold)
    if  percentdiff <= tolerance:
        print("Exit iterations in velocity potential because tolerance met ")
        print("Iterations =" , iter+1 ) ;
        tolflag = True
        break
    headold = update(head,headold)
print("End Calculations")
print("Iterations    = ",iter+1)
print("Closure Error = ",round(percentdiff,3))
print("Head Map")
print("----")
writearray(head)
print("----")

Exit iterations in velocity potential because tolerance met 
Iterations = 7972
End Calculations
Iterations    =  7972
Closure Error =  0.0
Head Map
----
[100.     99.758  99.513  99.259  98.995  98.715  98.417  98.098  97.755
383  96.9    96.329  95.729  95.167  94.674  94.159  93.617  93.053
468  91.866  91.252  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.715  98.416  98.097  97.755
383  96.9    96.329  95.728  95.167  94.674  94.158  93.617  93.053
468  91.866  91.252  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.714  98.416  98.097  97.754
383  96.9    96.329  95.727  95.166  94.674  94.158  93.617  93.052
468  91.866  91.251  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.714  98.416  98.097  97.754
385  96.901  96.329  95.726  95.164  94.674  94.158  93.617  93.052
468  91.866  91.251  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.714  98.416  98.097  97.754
387  96.903  96.328  95.724  95.161  94.673  94.158  93.617  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
39   96.908  96.328  95.718  95.156  94.673  94.158  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
392  97.39   96.328  95.156  95.154  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
39   96.908  96.328  95.718  95.156  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.754
386  96.903  96.328  95.723  95.16   94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.754
384  96.901  96.328  95.725  95.163  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.753
382  96.899  96.328  95.726  95.165  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.753
381  96.899  96.328  95.727  95.166  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
382  96.899  96.328  95.727  95.166  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
----

Now when you run the script, it seems to take a long time and many iterations. This observation is indeed correct – the ratio of conductivity terms and spatial discretiza- tion exerts a lot of influence on how fast the script can find a solution. This problem exists for most iterative methods. One could use linear solver packages, and simply solve the linear system without regard to structure, but assembly of the system matrix is non-trivial. The head “array” would need to be addressed as a vector (we can use pointers to accomplish this task — not too hard, but we would need to build the coefficient matrix, solve the system, and de-construct the result).

Generalizing the Boundary Conditions¶

In the prior examples the boundary conditions for the problems were kind of glossed over. We applied a fixed head boundary on the left and right edges of the rectangular domain, and zero-flux boundary at the top and bottom edges. A useful improvement is to allow the user to choose which type by supplying information in the input file. I find the easiest way (as we are just learning) is to assume the entire model is always surrounded by a constant head condition and use a mask to tell the program when that is not true.

The code fragments for making this change are pretty straightforward, and are dis- played in the listing below. We need to read in boundary indicators for the top, bottom, left, and right boundaries. Then convert them into numeric values for later. Here I choose to use a zero to indicate a zero-flux boundary and any non-zero (usually a 1) to indicate a fixed head boundary.

Next we apply the conditions within the solver loop by assigning the compued value of the adjacent cell (either above, below, left, or right as appropriate). The remainder of the script is unchanged, of course we need to include the new input values in the data file - I chose to insert the boundary mask just before the head array read.

input2GB contents

1
10
1
13
23
1e-5 
9000
15 25 35 45 55 65 75 85 95 105 115 125 135 145 155 165 175 185 195 205 215 225
5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 
1 1 1 1 1 1 1 1 1 1 1 1 
1 1 1 1 1 1 1 1 1 1 1 1 
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 100 90
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 0.0001 0.0001 0.0001 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10
10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10

def sse(matrix1,matrix2):
    sse=0.0
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            sse=sse+(matrix1[ir][jc]-matrix2[ir][jc])**2
    return(sse)

def update(matrix1,matrix2):
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    ##print(nr,nc)
    for ir in range(nr):
        for jc in range(nc):
            ##print(ir,jc)
            matrix2[ir][jc]=matrix1[ir][jc]
    return(matrix2)

def writearray(matrix):
    nr=len(matrix) # get row count
    nc=len(matrix[0]) # get column count
    import numpy as np
    new_list = list(np.around(np.array(matrix), 3))    
    for ir in range(nr):
        print(ir,new_list[ir][:])
    return()

localfile = open("input2GB.txt","r") # connect and read file for 2D gw model
deltax = float(localfile.readline())
deltay = float(localfile.readline())
deltaz = float(localfile.readline())
nrows = int(localfile.readline())
ncols = int(localfile.readline())
tolerance = float(localfile.readline())
maxiter = int(localfile.readline())
distancex = [] # empty list
distancex.append([float(n) for n in localfile.readline().strip().split()])
distancey = [] # empty list
distancey.append([float(n) for n in localfile.readline().strip().split()])
boundarytop = [] #empty list
boundarytop.append([float(n) for n in localfile.readline().strip().split()])
boundarybottom = [] #empty list
boundarybottom.append([int(n) for n in localfile.readline().strip().split()])
boundaryleft = [] #empty list
boundaryleft.append([int(n) for n in localfile.readline().strip().split()])
boundaryright = [] #empty list
boundaryright.append([int(n) for n in localfile.readline().strip().split()])
head =[] # empty list
for irow in range(nrows):
        head.append([float(n) for n in localfile.readline().strip().split()])
hydcondx = [] # empty list
for irow in range(nrows):
        hydcondx.append([float(n) for n in localfile.readline().strip().split()])
hydcondy = [] # empty list
for irow in range(nrows):
        hydcondy.append([float(n) for n in localfile.readline().strip().split()])
localfile.close() # Disconnect the file
##
amat = [[0 for j in range(ncols)] for i in range(nrows)]
bmat = [[0 for j in range(ncols)] for i in range(nrows)]
cmat = [[0 for j in range(ncols)] for i in range(nrows)]
dmat = [[0 for j in range(ncols)] for i in range(nrows)]
##
for irow in range(1,nrows-1):
    for jcol in range(1,ncols-1):
        amat[irow][jcol] = (( hydcondx[irow-1][jcol  ]+ hydcondx[irow  ][jcol  ]) * deltaz ) /(2.0*deltax**2)
        bmat[irow][jcol] = (( hydcondx[irow  ][jcol  ]+ hydcondx[irow+1][jcol  ]) * deltaz ) /(2.0*deltax**2)
        cmat[irow][jcol] = (( hydcondy[irow  ][jcol-1]+ hydcondy[irow  ][jcol  ]) * deltaz ) /(2.0*deltay**2)
        dmat[irow][jcol] = (( hydcondy[irow  ][jcol  ]+ hydcondy[irow  ][jcol+1]) * deltaz ) /(2.0*deltay**2)
##
headold = [[0 for jc in range(ncols)] for ir in range(nrows)] #force new matrix
headold = update(head,headold) # update
##writearray(head)
##print("----")
##writearray(headold)
##print("--------")
tolflag = False
for iter in range(maxiter):
##    print("begin iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
##    print("--------")

# Boundary Conditions

# first and last row special == no flow boundaries
    for jcol in range(ncols):
        if boundarytop[0][jcol] == 0: # no - flow at top
            head [0][jcol ] = head[1][jcol ]
        if boundarybottom[0][ jcol ] == 0: # no - flow at bottom
            head [nrows-1][jcol ] = head[nrows-2][jcol ]
# first and last column special == no flow boundaries     
    for irow in range(nrows): 
        if  boundaryleft[0][ irow ] == 0:
            head[irow][0] = head [irow][1] # no - flow at left
        if boundaryright[0][ irow ] == 0: 
            head [irow][ncols-1] = head[ irow ][ncols-2] # no - flow at right
# interior updates
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            head[irow][jcol]=( amat[irow][jcol]*head[irow-1][jcol  ] 
                              +bmat[irow][jcol]*head[irow+1][jcol  ] 
                              +cmat[irow][jcol]*head[irow  ][jcol-1] 
                              +dmat[irow][jcol]*head[irow  ][jcol+1])/(amat[ irow][jcol ]+ bmat[ irow][jcol ]+ cmat[ irow][jcol ]+ dmat[ irow][jcol ])
# test for stopping iterations
##    print("end iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
    percentdiff = sse(head,headold)
    if  percentdiff <= tolerance:
        print("Exit iterations in velocity potential because tolerance met ")
        print("Iterations =" , iter+1 ) ;
        tolflag = True
        break
    headold = update(head,headold)
print("End Calculations")
print("Iterations    = ",iter+1)
print("Closure Error = ",round(percentdiff,3))
print("Head Map")
print("----")
writearray(head)
print("----")

Exit iterations in velocity potential because tolerance met 
Iterations = 7972
End Calculations
Iterations    =  7972
Closure Error =  0.0
Head Map
----
[100.     99.758  99.513  99.259  98.995  98.715  98.417  98.098  97.755
383  96.9    96.329  95.729  95.167  94.674  94.159  93.617  93.053
468  91.866  91.252  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.715  98.416  98.097  97.755
383  96.9    96.329  95.728  95.167  94.674  94.158  93.617  93.053
468  91.866  91.252  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.714  98.416  98.097  97.754
383  96.9    96.329  95.727  95.166  94.674  94.158  93.617  93.052
468  91.866  91.251  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.714  98.416  98.097  97.754
385  96.901  96.329  95.726  95.164  94.674  94.158  93.617  93.052
468  91.866  91.251  90.628  90.   ]
[100.     99.758  99.513  99.259  98.994  98.714  98.416  98.097  97.754
387  96.903  96.328  95.724  95.161  94.673  94.158  93.617  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
39   96.908  96.328  95.718  95.156  94.673  94.158  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
392  97.39   96.328  95.156  95.154  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
39   96.908  96.328  95.718  95.156  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.754
386  96.903  96.328  95.723  95.16   94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.754
384  96.901  96.328  95.725  95.163  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.753
382  96.899  96.328  95.726  95.165  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.096  97.753
381  96.899  96.328  95.727  95.166  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
[100.     99.758  99.512  99.259  98.994  98.714  98.416  98.097  97.754
382  96.899  96.328  95.727  95.166  94.673  94.157  93.616  93.052
467  91.866  91.251  90.628  90.   ]
----

Contour Plotting¶

This is really a separate topic, but its a useful way to view output, so we will just append some code here.

# https://clouds.eos.ubc.ca/~phil/docs/problem_solving/06-Plotting-with-Matplotlib/06.14-Contour-Plots.html
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.griddata.html
# https://stackoverflow.com/questions/332289/how-do-you-change-the-size-of-figures-drawn-with-matplotlib
# https://stackoverflow.com/questions/18730044/converting-two-lists-into-a-matrix
# https://stackoverflow.com/questions/3242382/interpolation-over-an-irregular-grid
# https://stackoverflow.com/questions/33919875/interpolate-irregular-3d-data-from-a-xyz-file-to-a-regular-grid
# build XYZ structure from head map
my_xyz = [] # empty list
for irow in range(nrows):
    for jcol in range(ncols):
        my_xyz.append([distancex[0][jcol],distancey[0][irow],head[irow][jcol]])

import pandas
my_xyz = pandas.DataFrame(my_xyz) # convert into a data frame
#print(my_xyz) # activate to examine the dataframe
import numpy 
import matplotlib.pyplot
from scipy.interpolate import griddata
# extract lists from the dataframe
coord_x = my_xyz[0].values.tolist() # column 0 of dataframe
coord_y = my_xyz[1].values.tolist() # column 1 of dataframe
coord_z = my_xyz[2].values.tolist() # column 2 of dataframe
coord_xy = numpy.column_stack((coord_x, coord_y))
# Set plotting range in original data units
lon = numpy.linspace(min(coord_x), max(coord_x), 45)
lat = numpy.linspace(min(coord_y), max(coord_y), 21)
X, Y = numpy.meshgrid(lon, lat)
# Grid the data; use linear interpolation (choices are nearest, linear, cubic)
Z = griddata(numpy.array(coord_xy), numpy.array(coord_z), (X, Y), method='cubic')
# Build the map
fig, ax = matplotlib.pyplot.subplots()
fig.set_size_inches(14, 7)
CS = ax.contour(X, Y, Z, levels = 12)
ax.clabel(CS, inline=2, fontsize=16)
ax.set_title('Contour Plot from Gridded Data File')

Text(0.5, 1.0, 'Contour Plot from Gridded Data File')

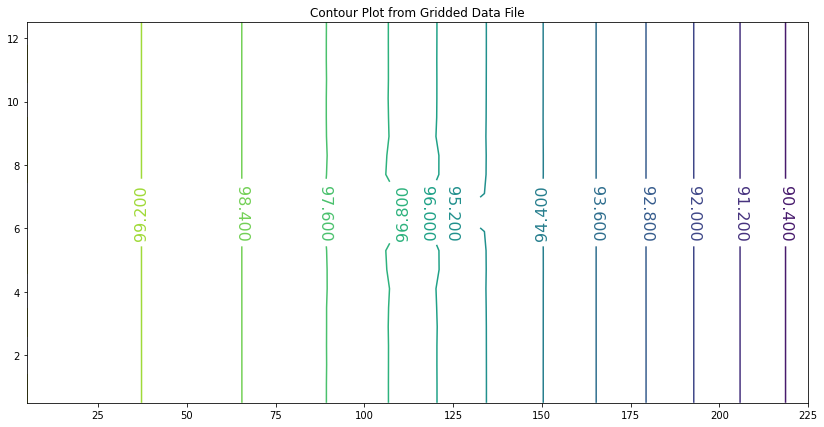
Addition of the generalized boundary conditions, and contour plotting expands the utility of our script as illustrated in the next example.

Homebrew - Example 3: Pore Pressure under a Dam¶

Fig. 22 is a schematic of a dam built upon a permeable ground layer 80 meters thick (segment A to I).

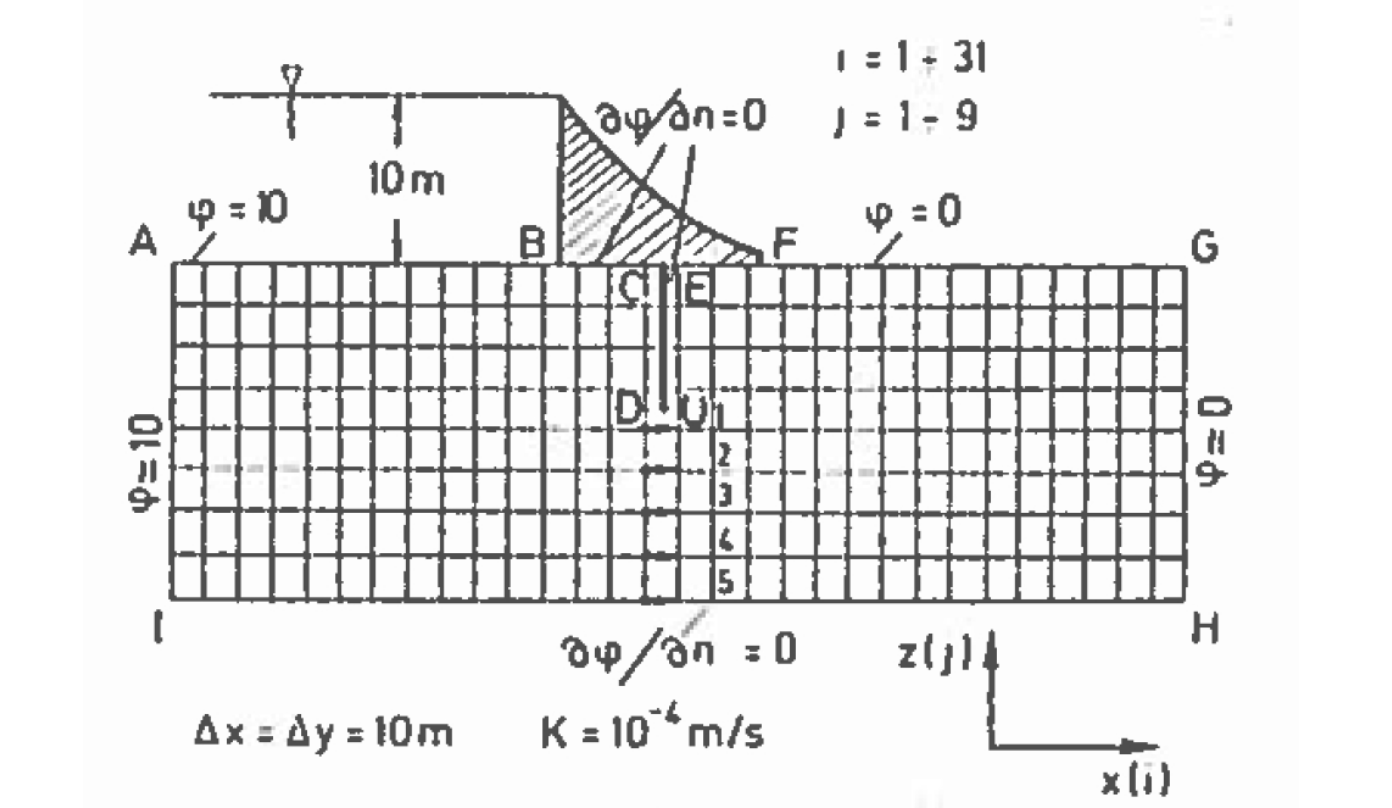
Fig. 22 Schematic of a dam on permeable soil with the sheet pile curtain underneath the dam.¶

The dam has a base 60 meters wide (segment B to F), with an upstream water depth of 10 meters. The downstream side of the dam is at 0 meters depth (otherwise its not a very good dam!). A sheetpile cutoff wall is installed beneath the dam (segment C to D to U to E). The ground layer has a hydraulic conductivity of K = 1 × 10−4 meters per second.

Important engineering questions are what is the pore water pressure under the dam, and is what is the total seepage under the dam? The pore water pressure can be found by solving for heads under the dam then subtracting the elevation of the computation location relative to a datum. The flow is found by Darcy’s law applied under the dam (shown as locations 1,2,3,4, and 5 in the sketch), which in turn requires computation of head under the dam. Thus the questions are answered by finding the head distribution under the dam.

The flow field (mathematically) extends an infinite distance upstream and downstream, but as a practical matter the contribution to seepage far upstream of the dam is negligible, and hence is approximated by the finite domain depicted.

Using the tools we have already built we can simply build an input file, run our script and determine the head distribution (and thus compute the discharges under the dam. There are two ways to conceptualize the model domain, we will examine both.

The first is to represent the domain as shown, and make the following specifications in the boundary condition information, and we will treat the sheetpile cutoff wall as a low permeability inclusion (much like the the prior example). The boundary conditions are:

The segment from A to B is a constant head boundary with value equal to 10.
The segment from B to F is a zero-flux boundary.
The segment from B to C to D to U to E to F should be treated as a zero-flux boundary, but our mask does not extend into the interior – however the sheetpile itself can be approximated by providing a very small permeability. Alternately we could (should) modify the code to handle interior boundaries – but that is outside the scope of this chapter.
The segment from F to G is a constant head boundary with value equal to 0.
The segment form G to H is a constant head boundary with value equal to 0.
The segment from H to I is a zero-flux boundary.
The segment from I to A is a constant head boundary with value equal to 10.

input3.txt contents

10
10
1
9
31
1e-12
5000
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300
70 60 50 40 30 20 10 0
1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
10 10 10 10 10 10 10 10 10 10 10 10 10 10 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.00010
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0000001 0.0000001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001
0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.0001 0.00010

def sse(matrix1,matrix2):
    sse=0.0
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            sse=sse+(matrix1[ir][jc]-matrix2[ir][jc])**2
    return(sse)

def update(matrix1,matrix2):
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    ##print(nr,nc)
    for ir in range(nr):
        for jc in range(nc):
            ##print(ir,jc)
            matrix2[ir][jc]=matrix1[ir][jc]
    return(matrix2)

def writearray(matrix):
    nr=len(matrix) # get row count
    nc=len(matrix[0]) # get column count
    import numpy as np
    new_list = list(np.around(np.array(matrix), 3))    
    for ir in range(nr):
        print(ir,new_list[ir][:])
    return()

localfile = open("input3.txt","r") # connect and read file for 2D gw model
deltax = float(localfile.readline())
deltay = float(localfile.readline())
deltaz = float(localfile.readline())
nrows = int(localfile.readline())
ncols = int(localfile.readline())
tolerance = float(localfile.readline())
maxiter = int(localfile.readline())
distancex = [] # empty list
distancex.append([float(n) for n in localfile.readline().strip().split()])
distancey = [] # empty list
distancey.append([float(n) for n in localfile.readline().strip().split()])
boundarytop = [] #empty list
boundarytop.append([float(n) for n in localfile.readline().strip().split()])
boundarybottom = [] #empty list
boundarybottom.append([int(n) for n in localfile.readline().strip().split()])
boundaryleft = [] #empty list
boundaryleft.append([int(n) for n in localfile.readline().strip().split()])
boundaryright = [] #empty list
boundaryright.append([int(n) for n in localfile.readline().strip().split()])
head =[] # empty list
for irow in range(nrows):
        head.append([float(n) for n in localfile.readline().strip().split()])
hydcondx = [] # empty list
for irow in range(nrows):
        hydcondx.append([float(n) for n in localfile.readline().strip().split()])
hydcondy = [] # empty list
for irow in range(nrows):
        hydcondy.append([float(n) for n in localfile.readline().strip().split()])
localfile.close() # Disconnect the file
##
amat = [[0 for j in range(ncols)] for i in range(nrows)]
bmat = [[0 for j in range(ncols)] for i in range(nrows)]
cmat = [[0 for j in range(ncols)] for i in range(nrows)]
dmat = [[0 for j in range(ncols)] for i in range(nrows)]
##
for irow in range(1,nrows-1):
    for jcol in range(1,ncols-1):
        amat[irow][jcol] = (( hydcondx[irow-1][jcol  ]+ hydcondx[irow  ][jcol  ]) * deltaz ) /(2.0*deltax**2)
        bmat[irow][jcol] = (( hydcondx[irow  ][jcol  ]+ hydcondx[irow+1][jcol  ]) * deltaz ) /(2.0*deltax**2)
        cmat[irow][jcol] = (( hydcondy[irow  ][jcol-1]+ hydcondy[irow  ][jcol  ]) * deltaz ) /(2.0*deltay**2)
        dmat[irow][jcol] = (( hydcondy[irow  ][jcol  ]+ hydcondy[irow  ][jcol+1]) * deltaz ) /(2.0*deltay**2)
##
headold = [[0 for jc in range(ncols)] for ir in range(nrows)] #force new matrix
headold = update(head,headold) # update
##writearray(head)
##print("----")
##writearray(headold)
##print("--------")
tolflag = False
for iter in range(maxiter):
##    print("begin iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
##    print("--------")

# Boundary Conditions

# first and last row special == no flow boundaries
    for jcol in range(ncols):
        if boundarytop[0][jcol] == 0: # no - flow at top
            head [0][jcol ] = head[1][jcol ]
        if boundarybottom[0][ jcol ] == 0: # no - flow at bottom
            head [nrows-1][jcol ] = head[nrows-2][jcol ]
# first and last column special == no flow boundaries     
    for irow in range(nrows): 
        if  boundaryleft[0][ irow ] == 0:
            head[irow][0] = head [irow][1] # no - flow at left
        if boundaryright[0][ irow ] == 0: 
            head [irow][ncols-1] = head[ irow ][ncols-2] # no - flow at right
# interior updates
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            head[irow][jcol]=( amat[irow][jcol]*head[irow-1][jcol  ] 
                              +bmat[irow][jcol]*head[irow+1][jcol  ] 
                              +cmat[irow][jcol]*head[irow  ][jcol-1] 
                              +dmat[irow][jcol]*head[irow  ][jcol+1])/(amat[ irow][jcol ]+ bmat[ irow][jcol ]+ cmat[ irow][jcol ]+ dmat[ irow][jcol ])
# test for stopping iterations
##    print("end iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
    percentdiff = sse(head,headold)
    if  percentdiff <= tolerance:
        print("Exit iterations in velocity potential because tolerance met ")
        print("Iterations =" , iter+1 ) ;
        tolflag = True
        break
    headold = update(head,headold)
print("End Calculations")
print("Iterations    = ",iter+1)
print("Closure Error = ",round(percentdiff,3))
print("Head Map")
print("----")
writearray(head)
print("----")

Exit iterations in velocity potential because tolerance met 
Iterations = 519
End Calculations
Iterations    =  519
Closure Error =  0.0
Head Map
----
[10.    10.    10.    10.    10.    10.    10.    10.    10.    10.
   10.     8.819  8.595  8.593  1.414  1.412  1.187  0.     0.
    0.     0.     0.     0.     0.     0.     0.     0.     0.
  ]
[10.     9.977  9.954  9.928  9.899  9.866  9.826  9.777  9.715  9.633
512  9.3    8.819  8.595  8.593  1.414  1.412  1.187  0.705  0.492
371  0.289  0.228  0.18   0.141  0.109  0.082  0.058  0.037  0.018
  ]
[10.     9.956  9.91   9.86   9.803  9.738  9.661  9.567  9.451  9.305
116  8.868  8.562  8.372  8.37   1.638  1.636  1.446  1.139  0.891
703  0.557  0.443  0.35   0.275  0.212  0.16   0.114  0.073  0.036
  ]
[10.     9.936  9.87   9.798  9.717  9.623  9.512  9.379  9.217  9.019
778  8.493  8.189  7.959  7.957  2.051  2.05   1.82   1.515  1.231
991  0.795  0.635  0.504  0.396  0.306  0.23   0.164  0.106  0.052
  ]
[10.     9.92   9.836  9.745  9.642  9.524  9.385  9.219  9.019  8.776
485  8.139  7.743  7.316  6.481  3.529  2.694  2.267  1.872  1.527
236  0.996  0.798  0.635  0.5    0.387  0.291  0.208  0.134  0.065
  ]
[10.     9.906  9.809  9.703  9.584  9.447  9.286  9.093  8.862  8.583
245  7.834  7.327  6.665  5.647  4.364  3.346  2.684  2.178  1.768
431  1.154  0.926  0.738  0.581  0.45   0.339  0.242  0.156  0.076
  ]
[10.     9.897  9.79   9.674  9.543  9.393  9.217  9.007  8.754  8.449
078  7.626  7.067  6.369  5.493  4.518  3.642  2.945  2.387  1.936
567  1.264  1.014  0.809  0.637  0.494  0.371  0.265  0.171  0.084
  ]
[10.     9.893  9.781  9.659  9.523  9.366  9.182  8.963  8.699  8.381
994  7.522  6.947  6.252  5.439  4.572  3.76   3.065  2.491  2.021
636  1.32   1.06   0.845  0.666  0.516  0.388  0.277  0.178  0.087
  ]
[10.     9.893  9.781  9.659  9.523  9.366  9.182  8.963  8.699  8.381
994  7.522  6.947  6.252  5.439  4.572  3.76   3.065  2.491  2.021
636  1.32   1.06   0.845  0.666  0.516  0.388  0.277  0.178  0.087
  ]
----

# https://clouds.eos.ubc.ca/~phil/docs/problem_solving/06-Plotting-with-Matplotlib/06.14-Contour-Plots.html
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.griddata.html
# https://stackoverflow.com/questions/332289/how-do-you-change-the-size-of-figures-drawn-with-matplotlib
# https://stackoverflow.com/questions/18730044/converting-two-lists-into-a-matrix
# https://stackoverflow.com/questions/3242382/interpolation-over-an-irregular-grid
# https://stackoverflow.com/questions/33919875/interpolate-irregular-3d-data-from-a-xyz-file-to-a-regular-grid
# build XYZ structure from head map
my_xyz = [] # empty list
for irow in range(nrows):
    for jcol in range(ncols):
        my_xyz.append([distancex[0][jcol],distancey[0][irow],head[irow][jcol]])
import pandas
my_xyz = pandas.DataFrame(my_xyz) # convert into a data frame
#print(my_xyz) # activate to examine the dataframe
import numpy 
import matplotlib.pyplot
from scipy.interpolate import griddata
# extract lists from the dataframe
coord_x = my_xyz[0].values.tolist() # column 0 of dataframe
coord_y = my_xyz[1].values.tolist() # column 1 of dataframe
coord_z = my_xyz[2].values.tolist() # column 2 of dataframe
coord_xy = numpy.column_stack((coord_x, coord_y))
# Set plotting range in original data units
lon = numpy.linspace(min(coord_x), max(coord_x), 300)
lat = numpy.linspace(min(coord_y), max(coord_y), 80)
X, Y = numpy.meshgrid(lon, lat)
# Grid the data; use linear interpolation (choices are nearest, linear, cubic)
Z = griddata(numpy.array(coord_xy), numpy.array(coord_z), (X, Y), method='cubic')
# Build the map
fig, ax = matplotlib.pyplot.subplots()
fig.set_size_inches(14, 7)
CS = ax.contour(X, Y, Z, levels = 12)
ax.clabel(CS, inline=2, fontsize=16)
ax.set_title('Contour Plot from Gridded Data File')

Text(0.5, 1.0, 'Contour Plot from Gridded Data File')

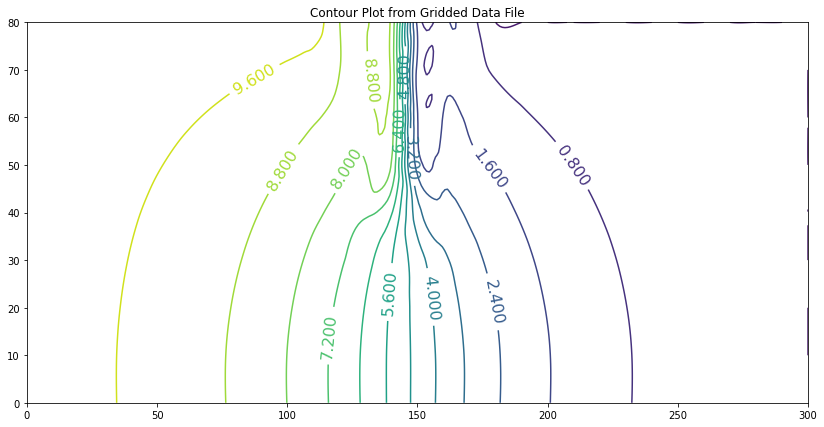
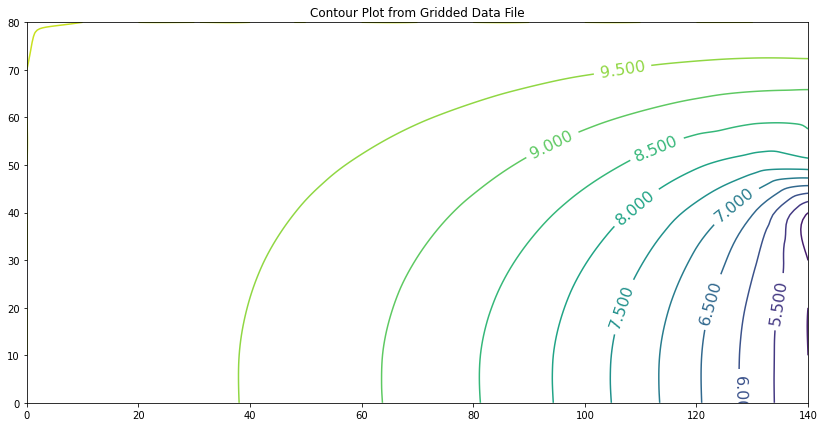
If we apply Darcy’s law to the portion in the vertical direction (where flow must be vertical to seep under the dam) the result is about \(3.76 m^3\) per day, per meter of width.

This example (like most roll-your-own) requires some specific knowledge of hydraulics to interpret the results, in this case knowing to apply Darcy’s law along the bottom of the reservoir to determine the flow rate, and to integrate (sum up) the individual cell flows to obtain total flow.

Homebrew - Example 4 : Pore Pressure under a Dam (Domain Decomposition approach)¶

The second way to solve this example, and perhaps better is to take advantage of the symmetry and cut the domain in half, as in Fig. 23.

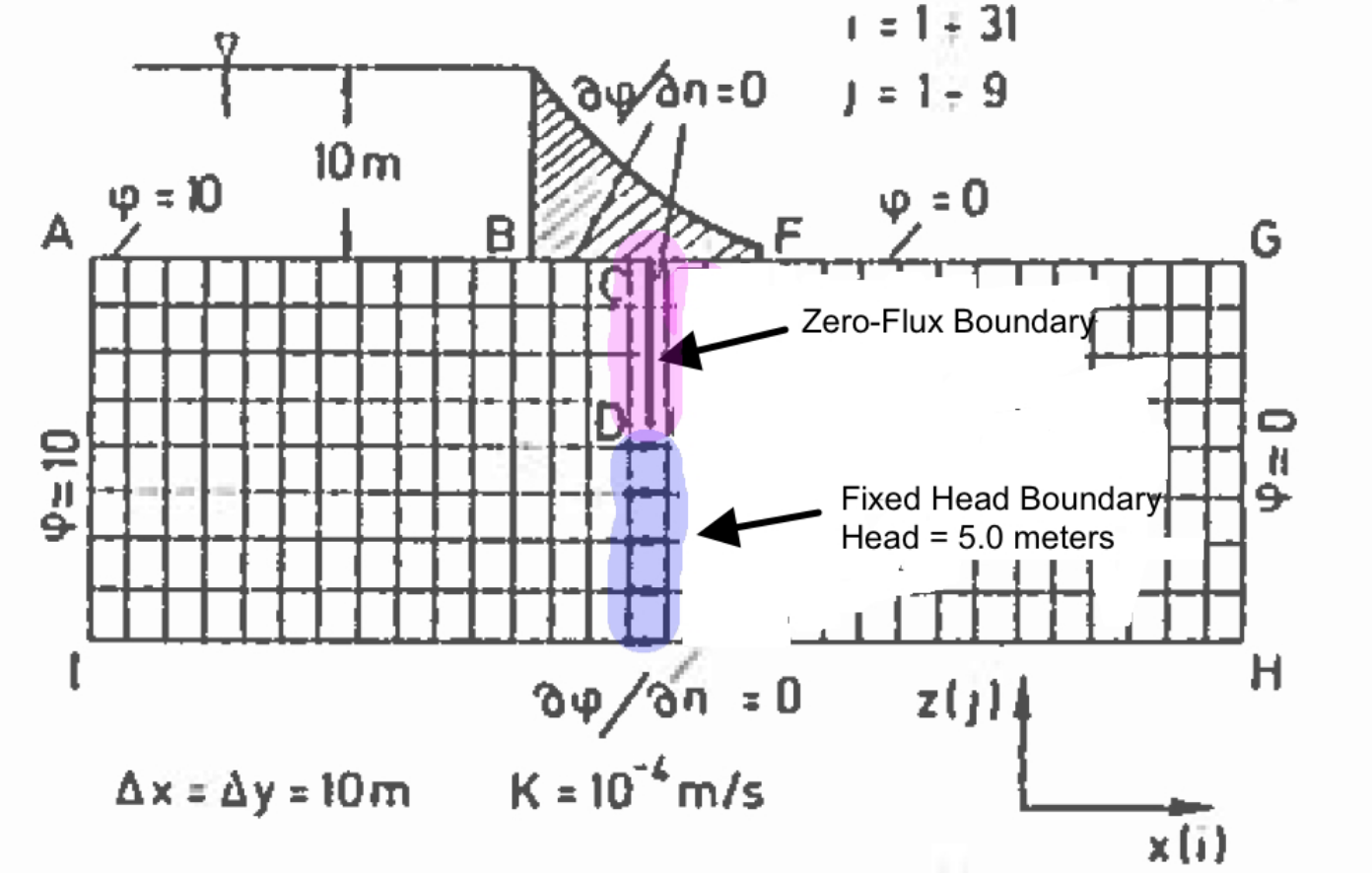
Fig. 23 Schematic of a dam on permeable soil with the sheet pile curtain underneath the dam.¶

In this method we can actually specify the sheetpile as a boundary, and we will obtain the same results, but only need to supply half as much input data.

def sse(matrix1,matrix2):
    sse=0.0
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            sse=sse+(matrix1[ir][jc]-matrix2[ir][jc])**2
    return(sse)

def update(matrix1,matrix2):
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    ##print(nr,nc)
    for ir in range(nr):
        for jc in range(nc):
            ##print(ir,jc)
            matrix2[ir][jc]=matrix1[ir][jc]
    return(matrix2)

def writearray(matrix):
    nr=len(matrix) # get row count
    nc=len(matrix[0]) # get column count
    import numpy as np
    new_list = list(np.around(np.array(matrix), 3))    
    for ir in range(nr):
        print(ir,new_list[ir][:])
    return()

localfile = open("input4.txt","r") # connect and read file for 2D gw model
deltax = float(localfile.readline())
deltay = float(localfile.readline())
deltaz = float(localfile.readline())
nrows = int(localfile.readline())
ncols = int(localfile.readline())
tolerance = float(localfile.readline())
maxiter = int(localfile.readline())
distancex = [] # empty list
distancex.append([float(n) for n in localfile.readline().strip().split()])
distancey = [] # empty list
distancey.append([float(n) for n in localfile.readline().strip().split()])
boundarytop = [] #empty list
boundarytop.append([float(n) for n in localfile.readline().strip().split()])
boundarybottom = [] #empty list
boundarybottom.append([int(n) for n in localfile.readline().strip().split()])
boundaryleft = [] #empty list
boundaryleft.append([int(n) for n in localfile.readline().strip().split()])
boundaryright = [] #empty list
boundaryright.append([int(n) for n in localfile.readline().strip().split()])
head =[] # empty list
for irow in range(nrows):
        head.append([float(n) for n in localfile.readline().strip().split()])
hydcondx = [] # empty list
for irow in range(nrows):
        hydcondx.append([float(n) for n in localfile.readline().strip().split()])
hydcondy = [] # empty list
for irow in range(nrows):
        hydcondy.append([float(n) for n in localfile.readline().strip().split()])
localfile.close() # Disconnect the file
##
amat = [[0 for j in range(ncols)] for i in range(nrows)]
bmat = [[0 for j in range(ncols)] for i in range(nrows)]
cmat = [[0 for j in range(ncols)] for i in range(nrows)]
dmat = [[0 for j in range(ncols)] for i in range(nrows)]
##
for irow in range(1,nrows-1):
    for jcol in range(1,ncols-1):
        amat[irow][jcol] = (( hydcondx[irow-1][jcol  ]+ hydcondx[irow  ][jcol  ]) * deltaz ) /(2.0*deltax**2)
        bmat[irow][jcol] = (( hydcondx[irow  ][jcol  ]+ hydcondx[irow+1][jcol  ]) * deltaz ) /(2.0*deltax**2)
        cmat[irow][jcol] = (( hydcondy[irow  ][jcol-1]+ hydcondy[irow  ][jcol  ]) * deltaz ) /(2.0*deltay**2)
        dmat[irow][jcol] = (( hydcondy[irow  ][jcol  ]+ hydcondy[irow  ][jcol+1]) * deltaz ) /(2.0*deltay**2)
##
headold = [[0 for jc in range(ncols)] for ir in range(nrows)] #force new matrix
headold = update(head,headold) # update
##writearray(head)
##print("----")
##writearray(headold)
##print("--------")
tolflag = False
for iter in range(maxiter):
##    print("begin iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
##    print("--------")

# Boundary Conditions

# first and last row special == no flow boundaries
    for jcol in range(ncols):
        if boundarytop[0][jcol] == 0: # no - flow at top
            head [0][jcol ] = head[1][jcol ]
        if boundarybottom[0][ jcol ] == 0: # no - flow at bottom
            head [nrows-1][jcol ] = head[nrows-2][jcol ]
# first and last column special == no flow boundaries     
    for irow in range(nrows): 
        if  boundaryleft[0][ irow ] == 0:
            head[irow][0] = head [irow][1] # no - flow at left
        if boundaryright[0][ irow ] == 0: 
            head [irow][ncols-1] = head[ irow ][ncols-2] # no - flow at right
# interior updates
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            head[irow][jcol]=( amat[irow][jcol]*head[irow-1][jcol  ] 
                              +bmat[irow][jcol]*head[irow+1][jcol  ] 
                              +cmat[irow][jcol]*head[irow  ][jcol-1] 
                              +dmat[irow][jcol]*head[irow  ][jcol+1])/(amat[ irow][jcol ]+ bmat[ irow][jcol ]+ cmat[ irow][jcol ]+ dmat[ irow][jcol ])
# test for stopping iterations
##    print("end iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
    percentdiff = sse(head,headold)
    if  percentdiff <= tolerance:
        print("Exit iterations in velocity potential because tolerance met ")
        print("Iterations =" , iter+1 ) ;
        tolflag = True
        break
    headold = update(head,headold)
print("End Calculations")
print("Iterations    = ",iter+1)
print("Closure Error = ",round(percentdiff,3))
print("Head Map")
print("----")
writearray(head)
print("----")

Exit iterations in velocity potential because tolerance met 
Iterations = 412
End Calculations
Iterations    =  412
Closure Error =  0.0
Head Map
----
0 [10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10. 10.]
1 [10.     9.975  9.949  9.921  9.889  9.853  9.811  9.761  9.701  9.632
  9.552  9.466  9.384  9.329  9.329]
2 [10.     9.951  9.9    9.845  9.783  9.712  9.629  9.531  9.413  9.274
  9.111  8.928  8.742  8.602  8.602]
3 [10.     9.93   9.856  9.776  9.687  9.584  9.463  9.319  9.147  8.939
  8.69   8.393  8.056  7.734  7.734]
4 [10.     9.911  9.818  9.717  9.604  9.473  9.32   9.137  8.916  8.647
  8.316  7.9    7.353  6.544  5.   ]
5 [10.     9.896  9.788  9.67   9.538  9.385  9.206  8.992  8.733  8.416
  8.026  7.538  6.913  6.088  5.   ]
6 [10.     9.886  9.767  9.637  9.492  9.325  9.127  8.891  8.607  8.26
  7.835  7.313  6.672  5.895  5.   ]
7 [10.     9.881  9.756  9.621  9.469  9.293  9.087  8.84   8.543  8.181
  7.741  7.207  6.566  5.82   5.   ]
8 [10.     9.881  9.756  9.621  9.469  9.293  9.087  8.84   8.543  8.181
  7.741  7.207  6.566  5.82   5.   ]
----

# https://clouds.eos.ubc.ca/~phil/docs/problem_solving/06-Plotting-with-Matplotlib/06.14-Contour-Plots.html
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.griddata.html
# https://stackoverflow.com/questions/332289/how-do-you-change-the-size-of-figures-drawn-with-matplotlib
# https://stackoverflow.com/questions/18730044/converting-two-lists-into-a-matrix
# https://stackoverflow.com/questions/3242382/interpolation-over-an-irregular-grid
# https://stackoverflow.com/questions/33919875/interpolate-irregular-3d-data-from-a-xyz-file-to-a-regular-grid
# build XYZ structure from head map
my_xyz = [] # empty list
for irow in range(nrows):
    for jcol in range(ncols):
        my_xyz.append([distancex[0][jcol],distancey[0][irow],head[irow][jcol]])
import pandas
my_xyz = pandas.DataFrame(my_xyz) # convert into a data frame
#print(my_xyz) # activate to examine the dataframe
import numpy 
import matplotlib.pyplot
from scipy.interpolate import griddata
# extract lists from the dataframe
coord_x = my_xyz[0].values.tolist() # column 0 of dataframe
coord_y = my_xyz[1].values.tolist() # column 1 of dataframe
coord_z = my_xyz[2].values.tolist() # column 2 of dataframe
coord_xy = numpy.column_stack((coord_x, coord_y))
# Set plotting range in original data units
lon = numpy.linspace(min(coord_x), max(coord_x), 300)
lat = numpy.linspace(min(coord_y), max(coord_y), 80)
X, Y = numpy.meshgrid(lon, lat)
# Grid the data; use linear interpolation (choices are nearest, linear, cubic)
Z = griddata(numpy.array(coord_xy), numpy.array(coord_z), (X, Y), method='cubic')
# Build the map
fig, ax = matplotlib.pyplot.subplots()
fig.set_size_inches(14, 7)
CS = ax.contour(X, Y, Z, levels = 12)
ax.clabel(CS, inline=2, fontsize=16)
ax.set_title('Contour Plot from Gridded Data File')

Text(0.5, 1.0, 'Contour Plot from Gridded Data File')

If we repeat the flow calculations, this time along the portion at the bottom of the sheetpile, we obtain nearly the same result, \(3.74 m^3\) per day, per meter of width.

This second way of solving the problem is far more correct because we didn’t have to choose an artificial value to mimic the effect of the sheetpile

The next concept is to illustrate a means to approximate the effect of a localized source (recharge or an injection well) or sink (pumping well). To incorporate these kinds of inputs we add terms to the governing equation as

\[ S \frac{\partial h}{\partial t} = \frac{\partial}{\partial x}({T_x \frac{\partial h}{\partial x}}) + \frac{\partial}{\partial y}({T_y \frac{\partial h}{\partial y}}) + R - Q \]

where R and Q are recharge and pumping expressed in dimensions of \(\frac{L^3}{T}\).

The resulting difference equation is

\[ S \frac{\partial h_{i,j}}{\partial t} = [ \frac{1}{\Delta x} T_x \frac{h_{i−1,j} − h_{i,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j-1} − h_{i,j}}{\Delta y}]-[\frac{1}{\Delta x} T_x \frac{h_{i,j} − h_{i+1,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j} − h_{i,j+1}}{\Delta y}] + \frac{R_{i,j}}{\Delta x \Delta y} - \frac{Q_{i,j}}{\Delta x \Delta y}\]

At equilibrium the time derivative vanishes and we have

\[ 0 = [ \frac{1}{\Delta x} T_x \frac{h_{i−1,j} − h_{i,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j-1} − h_{i,j}}{\Delta y}]-[\frac{1}{\Delta x} T_x \frac{h_{i,j} − h_{i+1,j}}{\Delta x} + \frac{1}{\Delta y} T_y \frac{h_{i,j} − h_{i,j+1}}{\Delta y}] + \frac{R_{i,j}}{\Delta x \Delta y} - \frac{Q_{i,j}}{\Delta x \Delta y}\]

These additions are incorporated into our program by only adding a few code fragments in certain places. The next listing shows the various added components to handle a well field. Observe we can incorporate recharge as if it were a well with a negative pumping rate so for this document it is not considered separately, although in many practical cases that might be a preferable way to incorporate the process.

Note

To clarify, we are entering net pumping which is \(R-Q\) as a single value for each cell.

Homebrew - Example 5: Wells in a rectangular aquifer¶

Fig. 24 is a rectangular aquifer with 4 wells as shown.

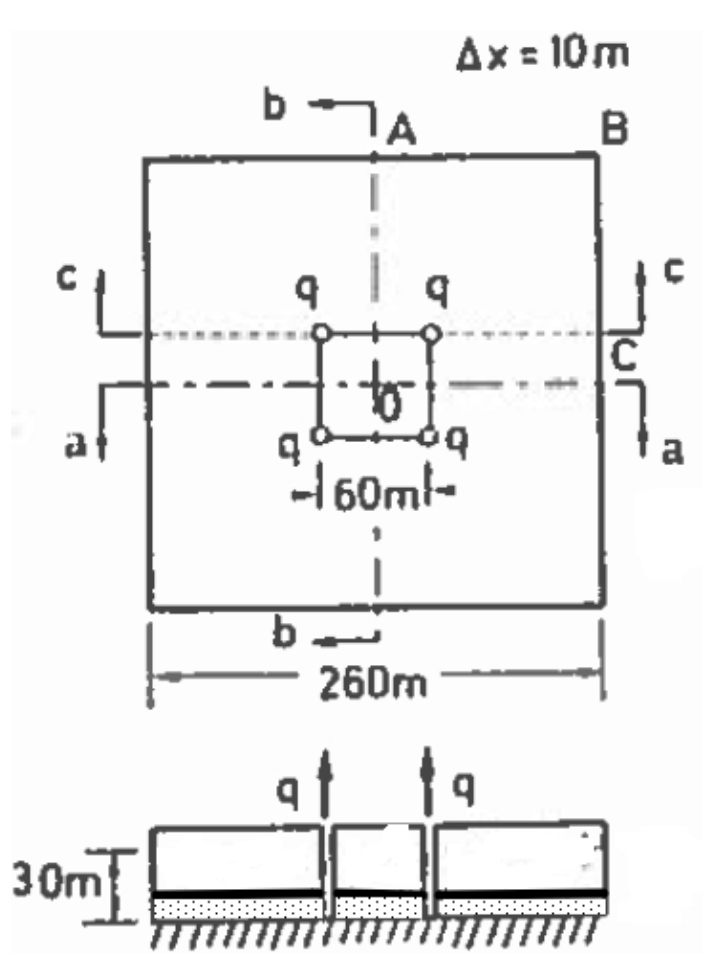
Fig. 24 Confined rectangular aquifer with 4 wells.¶

The aquifer thickness is 1 meters. The aquifer is surrounded with a constant head boundary of 30 meters. The hydraulic conductivity is \(K = 0.033\) m/day. Using a 10 meter × 10 meter grid spacing estimate the pumping rate in each well so that the head within the rectangular area defined by the well field is no smaller than 15 meters.

The script is modified to read an additional net pumping array just after the \(K_{x,y}\) terms.

The input file is a bit more complex because of its growing size; as the input requirements become substantial, one would write separate scripts just to build input files to structure them properly.

Note

We are essentially constructing a specialized database, and manually building that database can become tedious whereas we can automatically populate portions of the database with a script.

input5.txt contents

10
10
1
28
28
1e-9
5000
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270
10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30 30
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033 0.033
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.430 0.000 0.000 0.000 0.000 0.430 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.430 0.000 0.000 0.000 0.000 0.430 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000

The script is listed below:

def sse(matrix1,matrix2):
    sse=0.0
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            sse=sse+(matrix1[ir][jc]-matrix2[ir][jc])**2
    return(sse)

def update(matrix1,matrix2):
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    ##print(nr,nc)
    for ir in range(nr):
        for jc in range(nc):
            ##print(ir,jc)
            matrix2[ir][jc]=matrix1[ir][jc]
    return(matrix2)

def writearray(matrix):
    nr=len(matrix) # get row count
    nc=len(matrix[0]) # get column count
    import numpy as np
    new_list = list(np.around(np.array(matrix), 3))    
    for ir in range(nr):
        print(ir,new_list[ir][:])
    return()

localfile = open("input5.txt","r") # connect and read file for 2D gw model
deltax = float(localfile.readline())
deltay = float(localfile.readline())
deltaz = float(localfile.readline())
nrows = int(localfile.readline())
ncols = int(localfile.readline())
tolerance = float(localfile.readline())
maxiter = int(localfile.readline())
distancex = [] # empty list
distancex.append([float(n) for n in localfile.readline().strip().split()])
distancey = [] # empty list
distancey.append([float(n) for n in localfile.readline().strip().split()])
boundarytop = [] #empty list
boundarytop.append([float(n) for n in localfile.readline().strip().split()])
boundarybottom = [] #empty list
boundarybottom.append([int(n) for n in localfile.readline().strip().split()])
boundaryleft = [] #empty list
boundaryleft.append([int(n) for n in localfile.readline().strip().split()])
boundaryright = [] #empty list
boundaryright.append([int(n) for n in localfile.readline().strip().split()])
head =[] # empty list
for irow in range(nrows):
        head.append([float(n) for n in localfile.readline().strip().split()])
#writearray(head)
hydcondx = [] # empty list
for irow in range(nrows):
        hydcondx.append([float(n) for n in localfile.readline().strip().split()])
#writearray(hydcondx)
hydcondy = [] # empty list
for irow in range(nrows):
        hydcondy.append([float(n) for n in localfile.readline().strip().split()])
#writearray(hydcondy)
pumping = [] # empty list
for irow in range(nrows):
        pumping.append([float(n) for n in localfile.readline().strip().split()])
#writearray(pumping)
localfile.close() # Disconnect the file
##
amat = [[0 for j in range(ncols)] for i in range(nrows)]
bmat = [[0 for j in range(ncols)] for i in range(nrows)]
cmat = [[0 for j in range(ncols)] for i in range(nrows)]
dmat = [[0 for j in range(ncols)] for i in range(nrows)]
qrat = [[0 for j in range(ncols)] for i in range(nrows)]
## Transmissivity Arrays
for irow in range(1,nrows-1):
    for jcol in range(1,ncols-1):
        amat[irow][jcol] = (( hydcondx[irow-1][jcol  ]+ hydcondx[irow  ][jcol  ]) * deltaz ) /(2.0*deltax**2)
        bmat[irow][jcol] = (( hydcondx[irow  ][jcol  ]+ hydcondx[irow+1][jcol  ]) * deltaz ) /(2.0*deltax**2)
        cmat[irow][jcol] = (( hydcondy[irow  ][jcol-1]+ hydcondy[irow  ][jcol  ]) * deltaz ) /(2.0*deltay**2)
        dmat[irow][jcol] = (( hydcondy[irow  ][jcol  ]+ hydcondy[irow  ][jcol+1]) * deltaz ) /(2.0*deltay**2)
## Net Pumping Array
for irow in range(nrows):
    for jcol in range(ncols):
        qrat[irow][jcol] = (-1*pumping[irow][jcol]) /(deltax*deltay)
## Headold array
headold = [[0 for jc in range(ncols)] for ir in range(nrows)] #force a new matrix
headold = update(head,headold) # update
##writearray(head)
##print("----")
##writearray(headold)
##print("--------")
tolflag = False
for iter in range(maxiter):
##    print("begin iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
##    print("--------")

# Boundary Conditions

# first and last row special == no flow boundaries
    for jcol in range(ncols):
        if boundarytop[0][jcol] == 0: # no - flow at top
            head [0][jcol ] = head[1][jcol ]
        if boundarybottom[0][ jcol ] == 0: # no - flow at bottom
            head [nrows-1][jcol ] = head[nrows-2][jcol ]
# first and last column special == no flow boundaries     
    for irow in range(nrows): 
        if  boundaryleft[0][ irow ] == 0:
            head[irow][0] = head [irow][1] # no - flow at left
        if boundaryright[0][ irow ] == 0: 
            head [irow][ncols-1] = head[ irow ][ncols-2] # no - flow at right
# interior updates
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            head[irow][jcol]=(qrat[irow][jcol] 
                              +amat[irow][jcol]*head[irow-1][jcol  ] 
                              +bmat[irow][jcol]*head[irow+1][jcol  ] 
                              +cmat[irow][jcol]*head[irow  ][jcol-1] 
                              +dmat[irow][jcol]*head[irow  ][jcol+1])/(amat[ irow][jcol ]+ bmat[ irow][jcol ]+ cmat[ irow][jcol ]+ dmat[ irow][jcol ])
# test for stopping iterations
##    print("end iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
    percentdiff = sse(head,headold)
    if  percentdiff <= tolerance:
        print("Exit iterations in velocity potential because tolerance met ")
        print("Iterations =" , iter+1 ) ;
        tolflag = True
        break
    headold = update(head,headold)
print("End Calculations")
print("Iterations    = ",iter+1)
print("Closure Error = ",round(percentdiff,3))
# special messaging to report min head to adjust pump rates
import numpy
b = numpy.array(head)
print("Minimum Head",round(b.min(),3))
#
print("Head Map")
print("----")
writearray(head)
print("----")

Exit iterations in velocity potential because tolerance met 
Iterations = 806
End Calculations
Iterations    =  806
Closure Error =  0.0
Minimum Head 15.09
Head Map
----
[30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30.
30. 30. 30. 30. 30. 30. 30. 30. 30.]
[30.    29.914 29.828 29.743 29.659 29.577 29.499 29.426 29.36  29.303
258 29.225 29.206 29.202 29.211 29.235 29.271 29.318 29.374 29.436
503 29.572 29.643 29.715 29.787 29.858 29.929 30.   ]
[30.    29.827 29.655 29.484 29.315 29.15  28.992 28.844 28.71  28.595
502 28.436 28.398 28.389 28.409 28.457 28.531 28.627 28.74  28.867
002 29.143 29.286 29.43  29.574 29.716 29.858 30.   ]
[30.    29.74  29.481 29.223 28.968 28.717 28.476 28.248 28.042 27.864
721 27.619 27.56  27.547 27.579 27.654 27.769 27.918 28.094 28.29
497 28.711 28.928 29.145 29.361 29.575 29.788 30.   ]
[30.    29.653 29.306 28.96  28.615 28.275 27.945 27.632 27.346 27.098
899 26.757 26.677 26.66  26.705 26.811 26.973 27.183 27.429 27.7
985 28.277 28.57  28.862 29.151 29.436 29.719 30.   ]
[30.    29.566 29.131 28.695 28.258 27.823 27.397 26.988 26.611 26.282
019 25.835 25.732 25.711 25.771 25.911 26.129 26.411 26.739 27.096
466 27.841 28.214 28.582 28.943 29.299 29.651 30.   ]
[30.    29.48  28.957 28.43  27.898 27.363 26.831 26.313 25.828 25.401
061 24.83  24.706 24.681 24.755 24.935 25.221 25.593 26.021 26.477
943 27.407 27.863 28.308 28.742 29.167 29.585 30.   ]
[30.    29.396 28.787 28.17  27.541 26.901 26.252 25.606 24.986 24.431
995 23.719 23.58  23.552 23.633 23.851 24.228 24.72  25.273 25.849
422 26.982 27.522 28.044 28.549 29.041 29.523 30.   ]
[30.    29.317 28.626 27.922 27.196 26.446 25.67  24.873 24.079 23.344
769 22.47  22.344 22.312 22.375 22.61  23.118 23.784 24.505 25.223
915 26.575 27.201 27.798 28.37  28.924 29.465 30.   ]
[30.    29.245 28.479 27.693 26.877 26.018 25.107 24.137 23.115 22.095
268 21.048 21.013 20.979 20.945 21.096 21.85  22.795 23.738 24.622
442 26.201 26.909 27.576 28.21  28.82  29.414 30.   ]
[30.    29.183 28.353 27.496 26.599 25.642 24.604 23.453 22.147 20.653
161 19.44  19.681 19.645 19.332 18.978 20.393 21.807 23.028 24.088
028 25.878 26.659 27.386 28.074 28.732 29.37  30.   ]
[30.    29.134 28.253 27.341 26.379 25.347 24.213 22.925 21.368 19.208
281 17.872 18.626 18.589 17.758 15.09  18.937 21.012 22.481 23.673
704 25.624 26.462 27.238 27.967 28.662 29.336 30.   ]
[30.    29.1   28.184 27.234 26.231 25.154 23.976 22.667 21.19  19.531
916 18.139 18.364 18.325 18.022 17.719 19.252 20.824 22.209 23.42
491 25.452 26.327 27.135 27.893 28.615 29.313 30.   ]
[30.    29.083 28.149 27.18  26.157 25.061 23.872 22.577 21.193 19.812
711 18.405 18.364 18.325 18.286 18.511 19.528 20.821 22.112 23.307
388 25.366 26.259 27.083 27.856 28.591 29.301 30.   ]
[30.    29.083 28.149 27.18  26.157 25.061 23.872 22.577 21.193 19.812
711 18.405 18.364 18.325 18.286 18.511 19.528 20.821 22.112 23.307
388 25.366 26.259 27.083 27.856 28.591 29.301 30.   ]
[30.    29.1   28.184 27.234 26.231 25.154 23.976 22.667 21.19  19.531
916 18.139 18.364 18.325 18.022 17.719 19.252 20.824 22.209 23.42
491 25.452 26.327 27.135 27.893 28.615 29.313 30.   ]
[30.    29.134 28.253 27.341 26.379 25.347 24.213 22.925 21.368 19.208
281 17.872 18.626 18.589 17.758 15.09  18.937 21.012 22.481 23.673
704 25.624 26.462 27.238 27.967 28.662 29.336 30.   ]
[30.    29.183 28.353 27.496 26.599 25.642 24.604 23.453 22.147 20.653
161 19.44  19.681 19.645 19.332 18.978 20.393 21.807 23.028 24.088
028 25.878 26.659 27.386 28.074 28.732 29.37  30.   ]
[30.    29.245 28.479 27.693 26.877 26.018 25.107 24.137 23.115 22.095
268 21.048 21.013 20.979 20.945 21.096 21.85  22.795 23.738 24.622
442 26.201 26.909 27.576 28.21  28.82  29.414 30.   ]
[30.    29.317 28.626 27.922 27.196 26.446 25.67  24.873 24.079 23.344
769 22.47  22.344 22.312 22.375 22.61  23.118 23.784 24.504 25.223
915 26.575 27.201 27.798 28.37  28.924 29.465 30.   ]
[30.    29.396 28.787 28.17  27.541 26.901 26.252 25.606 24.986 24.431
995 23.719 23.58  23.552 23.633 23.851 24.228 24.72  25.273 25.849
422 26.982 27.522 28.044 28.549 29.041 29.523 30.   ]
[30.    29.48  28.957 28.43  27.898 27.363 26.831 26.313 25.828 25.401
061 24.83  24.706 24.681 24.755 24.935 25.221 25.593 26.021 26.477
943 27.407 27.863 28.308 28.742 29.167 29.585 30.   ]
[30.    29.566 29.131 28.695 28.258 27.823 27.397 26.988 26.611 26.282
019 25.835 25.732 25.711 25.771 25.911 26.129 26.411 26.739 27.096
466 27.841 28.214 28.582 28.943 29.299 29.651 30.   ]
[30.    29.653 29.306 28.96  28.615 28.275 27.945 27.632 27.346 27.098
899 26.757 26.677 26.66  26.705 26.811 26.973 27.183 27.429 27.7
985 28.277 28.57  28.862 29.151 29.436 29.719 30.   ]
[30.    29.74  29.481 29.223 28.968 28.717 28.476 28.248 28.042 27.864
721 27.619 27.56  27.547 27.579 27.654 27.769 27.918 28.094 28.29
497 28.711 28.928 29.145 29.361 29.575 29.788 30.   ]
[30.    29.827 29.655 29.484 29.315 29.15  28.992 28.844 28.71  28.595
502 28.436 28.398 28.389 28.409 28.457 28.531 28.627 28.74  28.867
002 29.143 29.286 29.43  29.574 29.716 29.858 30.   ]
[30.    29.914 29.828 29.743 29.659 29.577 29.499 29.426 29.36  29.303
258 29.225 29.206 29.202 29.211 29.235 29.271 29.318 29.374 29.436
503 29.572 29.643 29.715 29.787 29.858 29.929 30.   ]
[30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30.
30. 30. 30. 30. 30. 30. 30. 30. 30.]
----

Then the contour plot

# https://clouds.eos.ubc.ca/~phil/docs/problem_solving/06-Plotting-with-Matplotlib/06.14-Contour-Plots.html
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.griddata.html
# https://stackoverflow.com/questions/332289/how-do-you-change-the-size-of-figures-drawn-with-matplotlib
# https://stackoverflow.com/questions/18730044/converting-two-lists-into-a-matrix
# https://stackoverflow.com/questions/3242382/interpolation-over-an-irregular-grid
# https://stackoverflow.com/questions/33919875/interpolate-irregular-3d-data-from-a-xyz-file-to-a-regular-grid
# build XYZ structure from head map
my_xyz = [] # empty list
for irow in range(nrows):
    for jcol in range(ncols):
        my_xyz.append([distancex[0][jcol],distancey[0][irow],head[irow][jcol]])
import pandas
my_xyz = pandas.DataFrame(my_xyz) # convert into a data frame
#print(my_xyz) # activate to examine the dataframe
import numpy 
import matplotlib.pyplot
from scipy.interpolate import griddata
# extract lists from the dataframe
coord_x = my_xyz[0].values.tolist() # column 0 of dataframe
coord_y = my_xyz[1].values.tolist() # column 1 of dataframe
coord_z = my_xyz[2].values.tolist() # column 2 of dataframe
coord_xy = numpy.column_stack((coord_x, coord_y))
# Set plotting range in original data units
lon = numpy.linspace(min(coord_x), max(coord_x), 300)
lat = numpy.linspace(min(coord_y), max(coord_y), 80)
X, Y = numpy.meshgrid(lon, lat)
# Grid the data; use linear interpolation (choices are nearest, linear, cubic)
Z = griddata(numpy.array(coord_xy), numpy.array(coord_z), (X, Y), method='cubic')
# Build the map
fig, ax = matplotlib.pyplot.subplots()
fig.set_size_inches(14, 7)
CS = ax.contour(X, Y, Z, levels = 15)
ax.clabel(CS, inline=2, fontsize=16)
ax.set_title('Contour Plot from Gridded Data File')

Text(0.5, 1.0, 'Contour Plot from Gridded Data File')

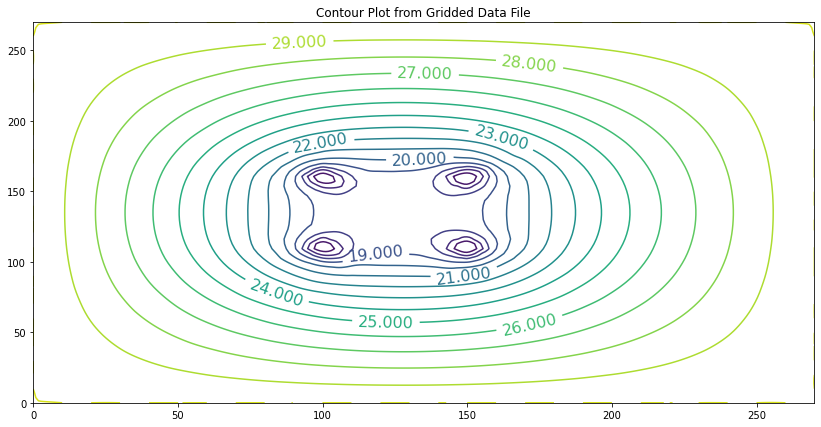
The contour plot shows the “cone of depression” around the well field. The script has an added message that reports the smallest head, and that report was used to adjust the pumping rates at the four wells until the value is close to the prescribed 15 meters.

The value for a single well is \(0.430 m^3/day\) (using the units of hydraulic conductivity as a guide). If the goal was then to specify particular pumps, that flow value and the required lift would be used to specify and purchase pumps for the system. We will repeat the problem in the next section of the workbook, except the aquifer will be unconfined — we expect different results, but will be able to re-use the input file.

Unconfined Aquifer Flow¶

Unconfined aquifer flow is simply a replacement of the transmissivity term by the product of saturated thickness and hydraulic conductivity.

\[ S \frac{\partial h}{\partial t} = \frac{\partial}{\partial x}({K_x \bar h \frac{\partial h}{\partial x}}) + \frac{\partial}{\partial y}({K_y \bar h \frac{\partial h}{\partial y}}) + R - Q \]

As a difference equation it becomes

\[ S \frac{\partial h_{i,j}}{\partial t} = [ \frac{1}{\Delta x} K_x \bar h \frac{h_{i−1,j} − h_{i,j}}{\Delta x} + \frac{1}{\Delta y} K_y \bar h \frac{h_{i,j-1} − h_{i,j}}{\Delta y}]-[\frac{1}{\Delta x} K_x \bar h \frac{h_{i,j} − h_{i+1,j}}{\Delta x} + \frac{1}{\Delta y} K_y \bar h \frac{h_{i,j} − h_{i,j+1}}{\Delta y}] + \frac{R_{i,j}}{\Delta x \Delta y} - \frac{Q_{i,j}}{\Delta x \Delta y} \]

Using the same spatial variation scheme we have

\[\begin{split} A_{i,j} = \frac{1}{2∆x^2} (K_{x,(i−1,j)} h_{i−1,j} + K_{x,(i,j)} h_{i−1,j})\\ B_{i,j} = \frac{1}{2∆x^2} (K_{x,(i,j)} h_{i,j} + K_{x,(i+1,j)} h_{i+1,j})\\ C_{i,j} = \frac{1}{2∆y^2} (K_{y,(i,j−1)} h_{i,j-1} + K_{y,(i,j)} h_{i,j})\\ D_{i,j} = \frac{1}{2∆y^2} (K_{y,(i,j)} h_{i,j} + K_{y,(i,j+1)} h_{i,j+1})\\ \end{split}\]

As before we can explicitly write the cell equation for \(h_{i,j}\), however the system is non-linear so the A, B, C, D coefficients are themselves functions of the current cell values.

This difference equation represents an approximation to the governing flow equation, the accuracy depending on the cell size. Boundary conditions are applied directly into the analogs (another name for the difference equations) at appropriate locations on the computational grid. Also as in the one-dimensional case we can generate solutions either by iteration or solving the resulting non-linear system. Fortunately theses kinds of systems are pretty well conditioned and one can usually compute the \(A, B, C, D\) coefficients from the most recent value (in an iterative sense) of \(h\) and proceeds as if the system is linear and it usually eventually converges.

Note

The approach here is called the variable transmissivity approach – as long as there is not too much curvature in the head distribution or dramatic changes in material properties in adjacent cells the Jacobi iteration method already employed will function, albeit slowly compared to more elaborate methods. In this discourse we are satisfied with these relatively primitive constructs, and more sophisticated approaches are presented elsewhere.

Homebrew - Example 6: Wells in a rectangular unconfined aquifer¶

Fig. 25 is a rectangular aquifer with 4 wells as shown – the drawing is identi- cal to the previous example, except the aquifer is now an unconfined aquifer.

The saturated thickness before the pumps are turned on is 30 meters. The aquifer is sur- rounded with a constant head boundary of 30 meters. The hydraulic conductivity is K = 0.033 m/day.

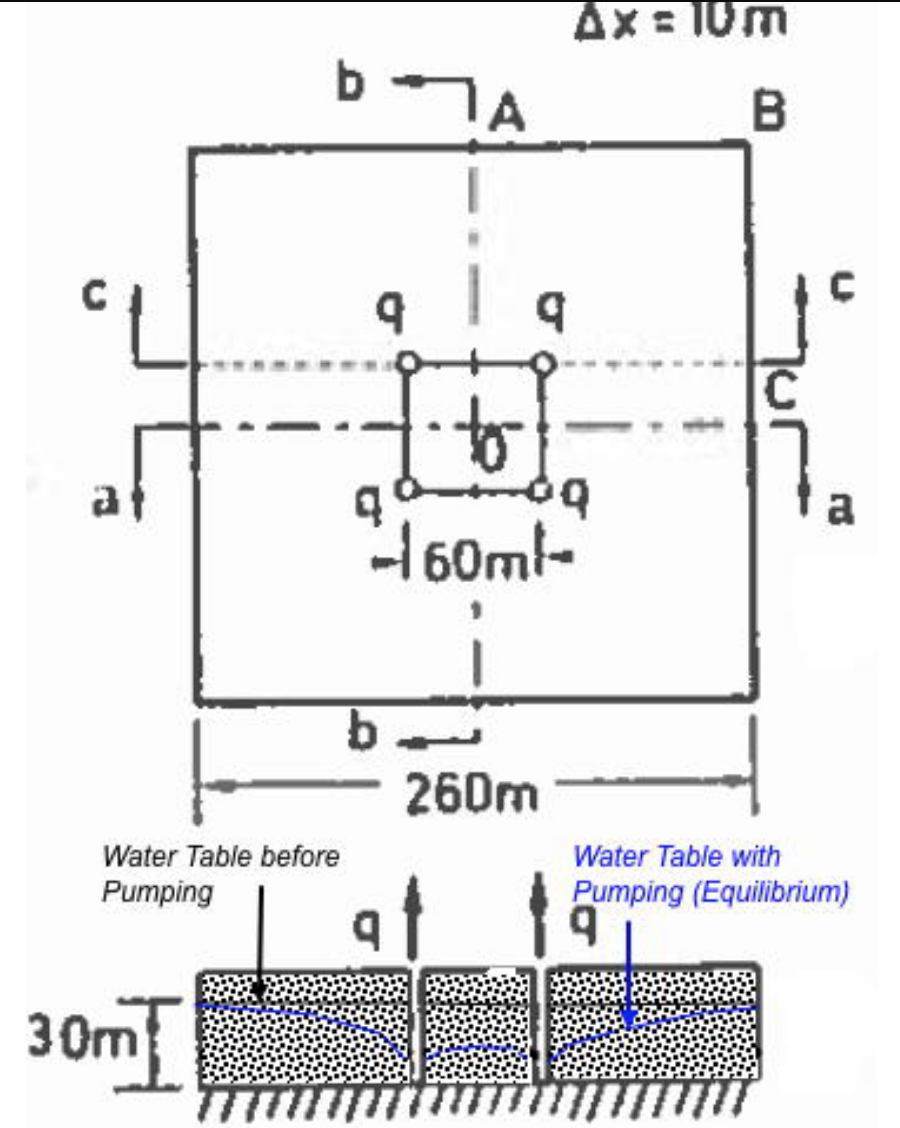
Fig. 25 Unconfined rectangular aquifer with 4 wells.¶

Using a 10 meter × 10 meter grid spacing estimate the pumping rate in each well so that the head within the rectangular area defined by the well field is no less than 15 meters. In this example, the pumping rates will be quite a bit larger because the saturated thickness at the desired drawdown is 15 times larger that the previous example.

The listing below is a script that performs the indicated computations. Upon initial inspection it appears nearly identical to the confined flow script, except the \(A, B, C, D\) computations are moved into the iteration loop, so they are updated after each iteration.

Observe that the \(∆z\) value is still read into the script, but never used. We are being somewhat lazy here; however it illustrates a code development protocol to re-use as much code as possible until the program functions as desired, then we could go back and delete unused components. I choose to retain the \(∆z\) so I would only have to change the input file pumping array and not create an entirely new input file structure. As stated earlier, as the problems get big, we would write scripts that build the input files before we run the computation engines.

input6.txt Relevant portion of the input file for the example. The remainder of the file is unchanged from the previous example (hence the reason I retained the ∆z variable).

000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 9.710 0.000 0.000 0.000 0.000 9.710 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 9.710 0.000 0.000 0.000 0.000 9.710 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000
000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000

def sse(matrix1,matrix2):
    sse=0.0
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    for ir in range(nr):
        for jc in range(nc):
            sse=sse+(matrix1[ir][jc]-matrix2[ir][jc])**2
    return(sse)

def update(matrix1,matrix2):
    nr=len(matrix1) # get row count
    nc=len(matrix1[0]) # get column count
    ##print(nr,nc)
    for ir in range(nr):
        for jc in range(nc):
            ##print(ir,jc)
            matrix2[ir][jc]=matrix1[ir][jc]
    return(matrix2)

def writearray(matrix):
    nr=len(matrix) # get row count
    nc=len(matrix[0]) # get column count
    import numpy as np
    new_list = list(np.around(np.array(matrix), 3))    
    for ir in range(nr):
        print(ir,new_list[ir][:])
    return()

localfile = open("input6.txt","r") # connect and read file for 2D gw model
deltax = float(localfile.readline())
deltay = float(localfile.readline())
deltaz = float(localfile.readline())
nrows = int(localfile.readline())
ncols = int(localfile.readline())
tolerance = float(localfile.readline())
maxiter = int(localfile.readline())
distancex = [] # empty list
distancex.append([float(n) for n in localfile.readline().strip().split()])
distancey = [] # empty list
distancey.append([float(n) for n in localfile.readline().strip().split()])
boundarytop = [] #empty list
boundarytop.append([float(n) for n in localfile.readline().strip().split()])
boundarybottom = [] #empty list
boundarybottom.append([int(n) for n in localfile.readline().strip().split()])
boundaryleft = [] #empty list
boundaryleft.append([int(n) for n in localfile.readline().strip().split()])
boundaryright = [] #empty list
boundaryright.append([int(n) for n in localfile.readline().strip().split()])
head =[] # empty list
for irow in range(nrows):
        head.append([float(n) for n in localfile.readline().strip().split()])
#writearray(head)
hydcondx = [] # empty list
for irow in range(nrows):
        hydcondx.append([float(n) for n in localfile.readline().strip().split()])
#writearray(hydcondx)
hydcondy = [] # empty list
for irow in range(nrows):
        hydcondy.append([float(n) for n in localfile.readline().strip().split()])
#writearray(hydcondy)
pumping = [] # empty list
for irow in range(nrows):
        pumping.append([float(n) for n in localfile.readline().strip().split()])
#writearray(pumping)
localfile.close() # Disconnect the file
##
amat = [[0 for j in range(ncols)] for i in range(nrows)]
bmat = [[0 for j in range(ncols)] for i in range(nrows)]
cmat = [[0 for j in range(ncols)] for i in range(nrows)]
dmat = [[0 for j in range(ncols)] for i in range(nrows)]
qrat = [[0 for j in range(ncols)] for i in range(nrows)]
## Net Pumping Array
for irow in range(nrows):
    for jcol in range(ncols):
        qrat[irow][jcol] = (-1*pumping[irow][jcol]) /(deltax*deltay)
## Headold array
headold = [[0 for jc in range(ncols)] for ir in range(nrows)] #force a new matrix
headold = update(head,headold) # update
##writearray(head)
##print("----")
##writearray(headold)
##print("--------")
tolflag = False
for iter in range(maxiter):
##    print("begin iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
##    print("--------")
## Transmissivity Arrays
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            amat[irow][jcol] = ((head[irow-1][jcol  ] * hydcondx[irow-1][jcol  ]+ head[irow  ][jcol  ] * hydcondx[irow  ][jcol  ]) * deltaz ) /(2.0*deltax**2)
            bmat[irow][jcol] = ((head[irow  ][jcol  ] * hydcondx[irow  ][jcol  ]+ head[irow+1][jcol  ] * hydcondx[irow+1][jcol  ]) * deltaz ) /(2.0*deltax**2)
            cmat[irow][jcol] = ((head[irow  ][jcol-1] * hydcondy[irow  ][jcol-1]+ head[irow  ][jcol  ] * hydcondy[irow  ][jcol  ]) * deltaz ) /(2.0*deltay**2)
            dmat[irow][jcol] = ((head[irow  ][jcol  ] * hydcondy[irow  ][jcol  ]+ head[irow  ][jcol+1] * hydcondy[irow  ][jcol+1]) * deltaz ) /(2.0*deltay**2)

# Boundary Conditions

# first and last row special == no flow boundaries
    for jcol in range(ncols):
        if boundarytop[0][jcol] == 0: # no - flow at top
            head [0][jcol ] = head[1][jcol ]
        if boundarybottom[0][ jcol ] == 0: # no - flow at bottom
            head [nrows-1][jcol ] = head[nrows-2][jcol ]
# first and last column special == no flow boundaries     
    for irow in range(nrows): 
        if  boundaryleft[0][ irow ] == 0:
            head[irow][0] = head [irow][1] # no - flow at left
        if boundaryright[0][ irow ] == 0: 
            head [irow][ncols-1] = head[ irow ][ncols-2] # no - flow at right

# interior updates
    for irow in range(1,nrows-1):
        for jcol in range(1,ncols-1):
            head[irow][jcol]=(qrat[irow][jcol] 
                              +amat[irow][jcol]*head[irow-1][jcol  ] 
                              +bmat[irow][jcol]*head[irow+1][jcol  ] 
                              +cmat[irow][jcol]*head[irow  ][jcol-1] 
                              +dmat[irow][jcol]*head[irow  ][jcol+1])/(amat[ irow][jcol ]+ bmat[ irow][jcol ]+ cmat[ irow][jcol ]+ dmat[ irow][jcol ])
# test for stopping iterations
##    print("end iteration")
##    writearray(head)
##    print("----")
##    writearray(headold)
    percentdiff = sse(head,headold)
    if  percentdiff <= tolerance:
        print("Exit iterations in velocity potential because tolerance met ")
        print("Iterations =" , iter+1 ) ;
        tolflag = True
        break
    headold = update(head,headold)
print("End Calculations")
print("Iterations    = ",iter+1)
print("Closure Error = ",round(percentdiff,5))
# special messaging to report min head to adjust pump rates
import numpy
b = numpy.array(head)
print("Minimum Head",round(b.min(),3))
#
print("Head Map")
print("----")
writearray(head)
print("----")

Exit iterations in velocity potential because tolerance met 
Iterations = 807
End Calculations
Iterations    =  807
Closure Error =  0.0
Minimum Head 15.054
Head Map
----
[30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30.
30. 30. 30. 30. 30. 30. 30. 30. 30.]
[30.    29.935 29.87  29.806 29.742 29.68  29.62  29.564 29.514 29.471
436 29.411 29.396 29.393 29.4   29.418 29.446 29.482 29.525 29.572
623 29.676 29.73  29.785 29.839 29.893 29.947 30.   ]
[30.    29.87  29.739 29.609 29.48  29.354 29.232 29.117 29.013 28.923
851 28.799 28.769 28.762 28.778 28.815 28.873 28.948 29.036 29.135
24  29.348 29.458 29.568 29.677 29.786 29.893 30.   ]
[30.    29.804 29.607 29.409 29.213 29.018 28.83  28.651 28.488 28.346
232 28.15  28.104 28.093 28.119 28.179 28.271 28.39  28.53  28.684
847 29.014 29.182 29.35  29.515 29.679 29.84  30.   ]
[30.    29.738 29.473 29.207 28.939 28.672 28.411 28.161 27.931 27.729
567 27.451 27.385 27.371 27.408 27.495 27.628 27.799 27.998 28.216
443 28.674 28.904 29.131 29.354 29.572 29.788 30.   ]
[30.    29.672 29.339 29.001 28.659 28.314 27.972 27.64  27.33  27.057
837 26.681 26.594 26.576 26.627 26.746 26.929 27.165 27.436 27.728
028 28.328 28.624 28.913 29.194 29.468 29.736 30.   ]
[30.    29.606 29.204 28.794 28.374 27.945 27.512 27.083 26.675 26.311
018 25.817 25.708 25.686 25.751 25.908 26.157 26.476 26.838 27.219
603 27.98  28.346 28.698 29.037 29.366 29.686 30.   ]
[30.    29.542 29.073 28.589 28.088 27.569 27.032 26.487 25.953 25.466
076 24.826 24.699 24.673 24.748 24.946 25.284 25.72  26.202 26.693
174 27.635 28.073 28.49  28.887 29.269 29.639 30.   ]
[30.    29.481 28.947 28.392 27.81  27.194 26.541 25.854 25.152 24.482
947 23.663 23.542 23.512 23.572 23.796 24.273 24.885 25.531 26.158
749 27.3   27.814 28.294 28.747 29.179 29.595 30.   ]
[30.    29.426 28.833 28.21  27.549 26.836 26.058 25.203 24.27  23.302
487 22.264 22.229 22.194 22.16  22.313 23.064 23.971 24.843 25.635
346 26.989 27.576 28.116 28.621 29.098 29.556 30.   ]
[30.    29.379 28.733 28.052 27.32  26.517 25.618 24.583 23.352 21.86
26  20.569 20.832 20.793 20.45  20.055 21.59  23.021 24.19  25.159
989 26.718 27.37  27.964 28.513 29.03  29.522 30.   ]
[30.    29.341 28.655 27.927 27.138 26.265 25.272 24.093 22.586 20.313
339 18.768 19.655 19.612 18.631 15.054 20.009 22.228 23.673 24.784
706 26.502 27.207 27.843 28.428 28.976 29.496 30.   ]
[30.    29.315 28.601 27.84  27.015 26.099 25.059 23.85  22.408 20.669
821 19.087 19.351 19.306 18.948 18.583 20.361 22.036 23.413 24.553
519 26.355 27.095 27.76  28.37  28.939 29.478 30.   ]
[30.    29.302 28.573 27.797 26.953 26.018 24.964 23.765 22.411 20.973
752 19.399 19.352 19.306 19.26  19.522 20.665 22.033 23.319 24.448
427 26.282 27.038 27.718 28.34  28.92  29.469 30.   ]
[30.    29.302 28.573 27.797 26.953 26.018 24.964 23.765 22.411 20.973
752 19.399 19.352 19.306 19.26  19.522 20.665 22.033 23.319 24.448
427 26.282 27.038 27.718 28.34  28.92  29.469 30.   ]
[30.    29.315 28.601 27.84  27.015 26.099 25.059 23.85  22.408 20.669
821 19.087 19.351 19.306 18.948 18.583 20.361 22.036 23.413 24.553
519 26.355 27.095 27.76  28.37  28.939 29.478 30.   ]
[30.    29.341 28.655 27.927 27.138 26.265 25.272 24.093 22.586 20.313
338 18.768 19.655 19.612 18.631 15.054 20.009 22.228 23.673 24.784
706 26.502 27.207 27.843 28.428 28.976 29.496 30.   ]
[30.    29.379 28.733 28.052 27.32  26.517 25.618 24.583 23.352 21.86
26  20.569 20.832 20.793 20.45  20.055 21.59  23.021 24.19  25.159
989 26.718 27.37  27.964 28.513 29.03  29.522 30.   ]
[30.    29.426 28.833 28.21  27.549 26.836 26.058 25.203 24.27  23.302
487 22.264 22.229 22.194 22.16  22.313 23.064 23.971 24.843 25.635
346 26.989 27.575 28.116 28.621 29.098 29.556 30.   ]
[30.    29.481 28.947 28.392 27.81  27.194 26.541 25.854 25.152 24.482
947 23.663 23.542 23.512 23.572 23.796 24.273 24.885 25.531 26.158
749 27.3   27.814 28.294 28.747 29.179 29.595 30.   ]
[30.    29.542 29.073 28.589 28.088 27.569 27.032 26.487 25.953 25.466
076 24.826 24.699 24.673 24.748 24.946 25.284 25.72  26.202 26.693
174 27.635 28.073 28.49  28.887 29.269 29.639 30.   ]
[30.    29.606 29.204 28.794 28.374 27.945 27.512 27.083 26.675 26.311
018 25.817 25.708 25.686 25.751 25.908 26.157 26.476 26.838 27.219
603 27.98  28.346 28.698 29.037 29.366 29.686 30.   ]
[30.    29.672 29.339 29.001 28.659 28.314 27.972 27.64  27.33  27.057
837 26.681 26.594 26.576 26.627 26.746 26.929 27.165 27.436 27.728
028 28.328 28.624 28.913 29.194 29.468 29.736 30.   ]
[30.    29.738 29.473 29.207 28.939 28.672 28.411 28.161 27.931 27.729
567 27.451 27.385 27.371 27.408 27.495 27.628 27.799 27.998 28.216
443 28.674 28.904 29.131 29.354 29.572 29.788 30.   ]
[30.    29.804 29.607 29.409 29.213 29.018 28.83  28.651 28.488 28.346
232 28.15  28.104 28.093 28.118 28.179 28.271 28.39  28.53  28.684
847 29.014 29.182 29.35  29.515 29.679 29.84  30.   ]
[30.    29.87  29.739 29.609 29.48  29.354 29.232 29.117 29.013 28.923
851 28.799 28.769 28.762 28.778 28.815 28.873 28.948 29.036 29.135
24  29.348 29.458 29.568 29.677 29.786 29.893 30.   ]
[30.    29.935 29.87  29.806 29.742 29.68  29.62  29.564 29.514 29.471
436 29.411 29.396 29.393 29.4   29.418 29.446 29.482 29.525 29.572
623 29.676 29.73  29.785 29.839 29.893 29.947 30.   ]
[30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30. 30.
30. 30. 30. 30. 30. 30. 30. 30. 30.]
----

# https://clouds.eos.ubc.ca/~phil/docs/problem_solving/06-Plotting-with-Matplotlib/06.14-Contour-Plots.html
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.griddata.html
# https://stackoverflow.com/questions/332289/how-do-you-change-the-size-of-figures-drawn-with-matplotlib
# https://stackoverflow.com/questions/18730044/converting-two-lists-into-a-matrix
# https://stackoverflow.com/questions/3242382/interpolation-over-an-irregular-grid
# https://stackoverflow.com/questions/33919875/interpolate-irregular-3d-data-from-a-xyz-file-to-a-regular-grid
# build XYZ structure from head map
my_xyz = [] # empty list
for irow in range(nrows):
    for jcol in range(ncols):
        my_xyz.append([distancex[0][jcol],distancey[0][irow],head[irow][jcol]])
import pandas
my_xyz = pandas.DataFrame(my_xyz) # convert into a data frame
#print(my_xyz) # activate to examine the dataframe
import numpy 
import matplotlib.pyplot
from scipy.interpolate import griddata
# extract lists from the dataframe
coord_x = my_xyz[0].values.tolist() # column 0 of dataframe
coord_y = my_xyz[1].values.tolist() # column 1 of dataframe
coord_z = my_xyz[2].values.tolist() # column 2 of dataframe
coord_xy = numpy.column_stack((coord_x, coord_y))
# Set plotting range in original data units
lon = numpy.linspace(min(coord_x), max(coord_x), 300)
lat = numpy.linspace(min(coord_y), max(coord_y), 80)
X, Y = numpy.meshgrid(lon, lat)
# Grid the data; use linear interpolation (choices are nearest, linear, cubic)
Z = griddata(numpy.array(coord_xy), numpy.array(coord_z), (X, Y), method='cubic')
# Build the map
fig, ax = matplotlib.pyplot.subplots()
fig.set_size_inches(14, 7)
CS = ax.contour(X, Y, Z, levels = 15)
ax.clabel(CS, inline=2, fontsize=16)
ax.set_title('Contour Plot from Gridded Data File')

Text(0.5, 1.0, 'Contour Plot from Gridded Data File')

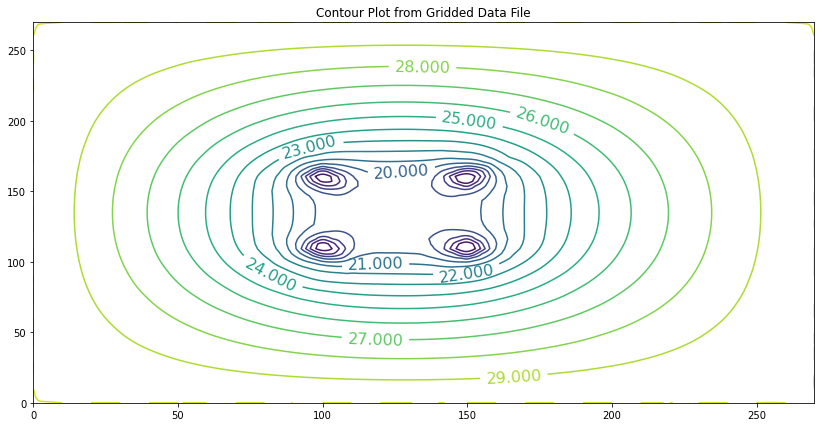
The plot is practically the same as in the previous example (in fact of the labels were not moved on the contour lines, the figures would look identical) however the pumping rate is 20 times larger for apparently the same head distribution — so if the dewatering effort were in an unconfined aquifer, perhaps for an excavation for a foundation, choosing the correct conditions would be kind of important.

Interim Summary¶

As a quick summary of this chapter we started with a 1D situation and built a finite-difference models to illustrate the structure for the Jacobi iteration method. Next we progressed to a 2D situation (it can either be a slice or a layer) and used the Jacobi iteration method.

Note

Using a formal linear solver would also work quite well, but the matrix assembly is a bit tedious – so that was left unaddressed.

Once we had the 2D computation engine working we extended capability by adding generalized boundary condition capability to the exterior boundaries (the same can be done for interior cells – the matrix assembly logic is awkward, so that too is left undone). Once the generalized boundary modification was built, we then added a recharge/pumping capability.

This last model is functionally useful (although it needs testing against known solutions to detect any coding errors). To complete the discussion, a simple modification using the variable transmissivity construct allowed us to extend our capability to unconfined aquifers. The next chapter will illustrate unsteady flow where the left hand side of the PDEs is no longer zero.

1D cases were not explicitly explored, however the tool so far can handle such cases by making the model 3 cells wide in the un-needed axis and it will accomplish the same goal (and avoid having separate codes for different dimensions).

Groundwater Hydrology

Groundwater Models¶

Storativity¶

Permeability¶

Head Loss Models¶

Equilibrium Models¶

Confined Aquifer Flow Modeling Theory¶

Solution Methods¶

Finite-Difference Methods – 1 Spatial Dimension¶

Finite-Difference Methods – 2 Spatial Dimensions¶

Homebrew - Example 1¶

Homebrew - Example 2¶

Generalizing the Boundary Conditions¶

Contour Plotting¶

Homebrew - Example 3: Pore Pressure under a Dam¶

Homebrew - Example 4 : Pore Pressure under a Dam (Domain Decomposition approach)¶

Homebrew - Example 5: Wells in a rectangular aquifer¶

Unconfined Aquifer Flow¶

Homebrew - Example 6: Wells in a rectangular unconfined aquifer¶

Interim Summary¶