Contents

Conservation of Angular Momentum

Lesson Outline

  • Definition of angular momentum

  • Example appliocation

Background

Angular momentum (moment of momentum) relates forces to changes in rotational velocity. Reynolds Transport Theorem is used to generate integral expressions of angular momentum balances in a control volume.

The ideas are fundamental in pumps, compressors, turbines, and similar machines.

Angular Momentum

../../_images/angular-p1-1.png

Caption

angular-p1-1 relates the extensive property of angular momentum for a system to the intensive property of moment of momentum per unit mass which is \(\bar r \times \bar V\).

../../_images/angular-p1-2.png

Caption

The result of application of the Reynolds Transport Theorem to the linear momentum term is an integral equation that relates the sum of external forces to the rate of change of linear momentum in the control volume plus the net momentum leaving across the control surface as depicted in angular-p1-2

Example 1: Application of Angular Momentum to a Reaction Turbine

Application of angular momentum often involves use of continunity and energy (bernoulli’s equation). Selection of CV is important to make analysis straightforward. Consider the following example involving a reaction turbine (like a Rain-Bird)

The problem statement is depicted in angular-ex1-1

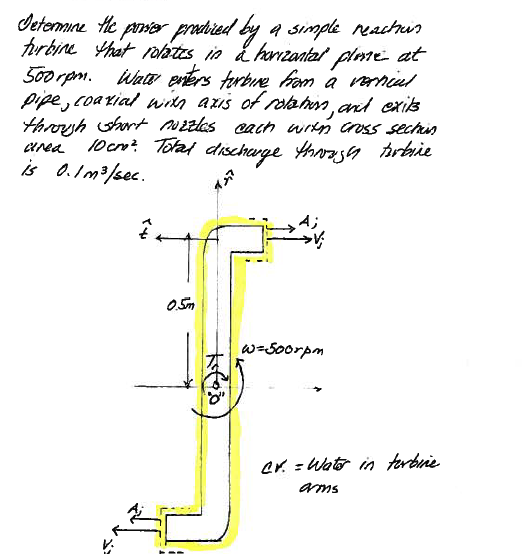
../../_images/angular-ex1-1.png

Caption

Apply continunity as in angular-ex1-2

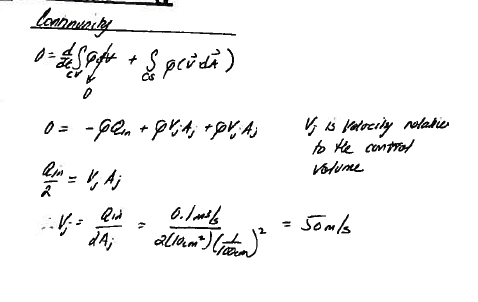
../../_images/angular-ex1-2.png

Caption

Then momentum as in angular-ex1-3

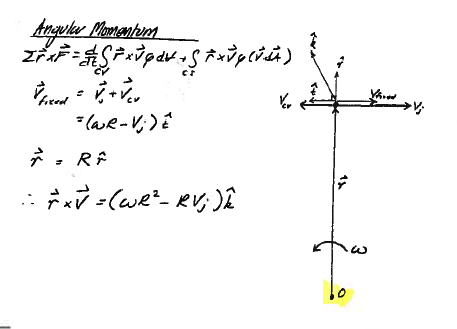
../../_images/angular-ex1-3.png

Caption

Continue the analysis (break the CV into upper and lower arm, use symmetry to cancel the volume integrals) as in angular-ex1-4

../../_images/angular-ex1-4.png

Caption

Complete the analysis as in angular-ex1-5

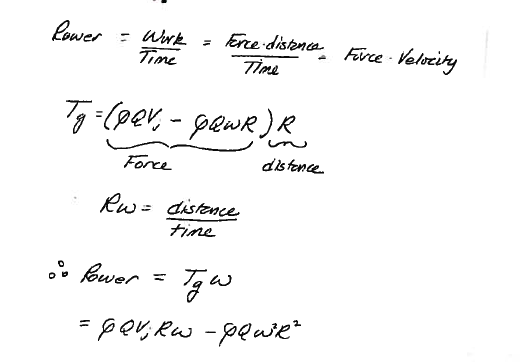
../../_images/angular-ex1-5.png

Caption

now apply ENGR-1330 to perform the calculations.

# computational thinning
import math
q = 0.1 #discharge
v_jet = 50.0
omega = 500*2*math.pi/60
radius = 0.5
rho = 1000.0
power = rho*q*v_jet*radius*omega - rho*q*omega**2*radius**2
print("Power ",round(power,2)," Newton-meters/sec    ")

Power  62360.77  Newton-meters/sec

Example 2: Application of Angular Momentum to a Reaction Turbine

Here we will do the same problem, but using a fixed reference frame CV

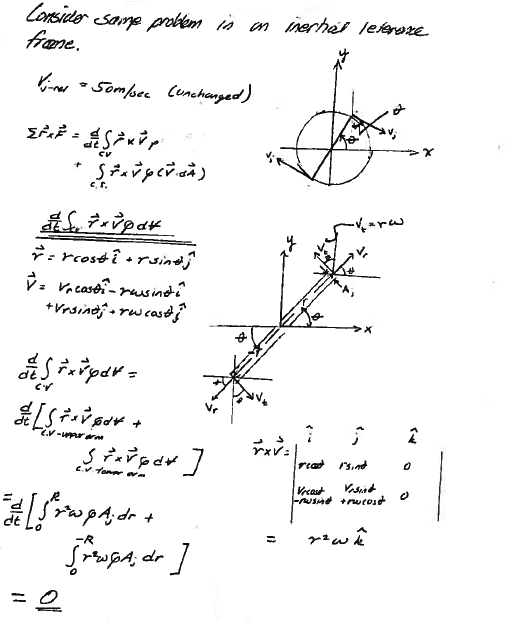
../../_images/angular-ex2-1.png

Caption

angular-ex1-5 is analysis of the volume integral in a vector representation of the moment of momentum

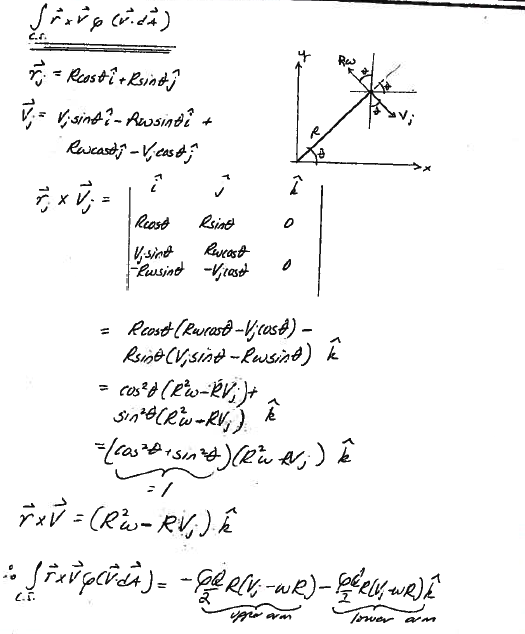
../../_images/angular-ex2-2.png

Caption

angular-ex1-5 is analysis of the flux integrals in a vector representation of the moment of momentum After the equations are constructed, the analysys proceedes the same as in the earlier example.

Readings

  1. CE-3305-2022-1 Syllabus. http://54.243.252.9/ce-3305-webroot/0-Syllabus/ce-3305-2022-1-syllabus.html

  2. Hibbeler, R.C, Fluid Mechanics, 2ed. Prentice Hall, 2018. ISBN: 9780134655413 pp. 293-355

  3. DF Elger, BC Williams, Crowe, CT and JA Roberson, Engineering Fluid Mechanics 10th edition, John Wiley & Sons, Inc., 2013. (placeholder file to get links working). http://54.243.252.9/ce-3305-webroot/3-Readings/EFM-9.pdf

  4. Cleveland, T. G. (2014) Fluid Mechanics Notes to Accompany CE 3305 at Jade-Holshule (TTU Study Abroad 2015-2019), Department of Civil, Environmental, and Construction Engineering, Whitacre College of Engineering. http://54.243.252.9/ce-3305-webroot/3-Readings/ce3305-lecture-9.pdf