Contents

Application of Drag

Example: Bang the Drum Slowly

Figure XX is a schematic of wind blowing on a traffic barrier drum (A 55-gallon drum painted orange). Estimate the wind speed needed to tip the drum over. The weight of the drum is 48 lbs, the diameter is 22.5 inches, and the height is 34.5 inches.

Figure XX. Traffic Barrier Drum

Step 1: Problem Statement

The statement above is good enough, to suppliment we will notice this is a fluids problem as well as a static problem.

Step 2: Sketch(s)

The first sketch is really a side view of the original conceptualization above.

Figure XX. Schematic of Situation

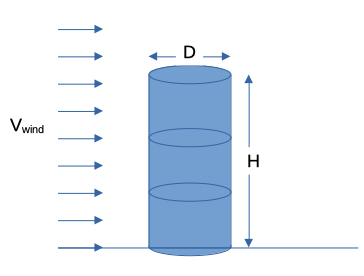
The next sketch is key, when the drum starts to tip over there is a moment of a single point of contact which is important to the analysis/

Figure XX. Drum at Moment of Tipping

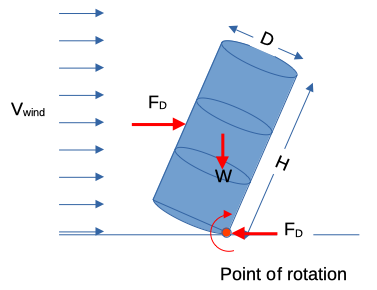
Step 3: List knowns and unknowns

Known:

  • Mass of drum

  • Dimensions of drum

  • Fluid (air)

  • Fluid properties (table look-up)

Unknown:

  • Wind speed to tip over drum as per drawing above

Step 4: Governing Principles

  • Drag force formula: \(F_D = C_D A \frac{\rho V^2}{2}\)

  • Static Force Balance: \(\sum F = 0\)

  • Static Moment Balance: \(\sum M_A = 0\)

Step 5: Analysis

From the force balance we conclude if the drum does not slide then at the point of contact the drag force forms the couple shown. The moment balance at the tipping point (see the pun there!) is

\(\sum M_A = 0 = W(\frac{D}{2}) - F_D (\frac{H}{2})\)

Do some of that algebra to obtain

\(W(\frac{D}{2}) = F_D (\frac{H}{2})\)

substutite in the definition of weight

\(mg(\frac{D}{2}) = F_D (\frac{H}{2})\)

more of that algebra and substitute in the drag force formula

\(mg(\frac{D}{H}) = C_D A \frac{\rho V^2}{2} \)

Next we will need a way to estimate \(C_D\) values and using the chart below should suffice.

Figure XX. $C_D$ Chart

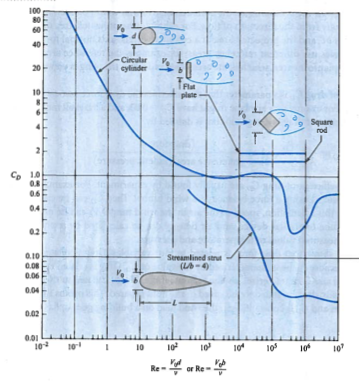
We will simply guess a value for \(C_D\) and solve for velocity, then check the Reynolds number and change the coefficient accordingly.

def drag(cd,area,rho,vel):
    drag = cd*area*rho*vel*vel*0.5
    return(drag)

def reynolds(velocity,diameter,viscosity,rho):
    reynolds = rho*velocity*diameter/viscosity
    return(reynolds)
######## problem data ###########
weightus = 48 # lbs, given
weightsi = weightus/2.2 # kilos
gravity  = 9.8 # ft/sec*sec
mass = weightsi
height = (34.5/12)/3.28 # meters
diameter = (22.5/12)/3.28 # meters
rho = 1.2 #kg/cu.m.
air_viscosity = 1.81e-05 #m^2/s
######### trial-error-correction ############
target = mass*gravity*(diameter/height)
area = diameter*height
cd = 0.38
vel = 34.9
print("Computed Drag Force = ",drag(cd,area,rho,vel),"Target Force = ",target)
print("Computed Reynolds Number = ",reynolds(vel,diameter,air_viscosity,rho))

Computed Drag Force =  139.14805320726128 Target Force =  139.44664031620553
Computed Reynolds Number =  1322682.2530656245

Our value above after a few manual iterations and updates is \(Re_D = 1.3 \times 10^6\) which produces a drag coefficient of \(C_D = 0.38\)

If we had a functional form for \(C_D\) we could simply incorporate it directly into the calculations above and use a quasi-Newton’s method to search for the velocity.

velmph = vel*3.28*3600/5280 # report in miles/hour
print("Estimated Velocity to Tip Barrel ",round(velmph,3)," mph")

Estimated Velocity to Tip Barrel  78.049  mph