Flow Patterns and Visualization¶
In real fluids, markers such as dye, smoke, heat are used to visualize how things flow.
The markers are tracers; the tracer hypothesis is that the tracer moves with the host fluid.
Some of the patterns are:
Timeline is a line formed by marking adjacent particles at some instant
Pathline is the trajectory of a particular fluid particle
Streakline is the trajectory of many particles that pass through some common point in space
Streamline is a line in a flow field that is tangent to velocity; no flow crosses a streamline (3D equivalent is called a streamtube)
In steady flow streamlines, streaklines, and pathlines are coincident. In unsteady (time-varying) flow this relationship is not preserved (and the three patterns will look different)
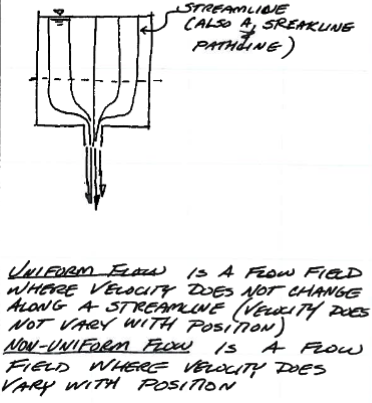
Flow in a tank with a holy bottom¶
Consider the flow depicted in the tank above; is the flow field uniform or non-uniform? What about the flow above the dashed line?
Flow dimensions are classified by how many space coordinates are required to speciofy the velocity field. All real flows are 3D, but useful results are possible with 2D and 1D approximations.
Velocity Field¶
Velocities are expressed in either a LaGrangian sense, or Eulerian sense.
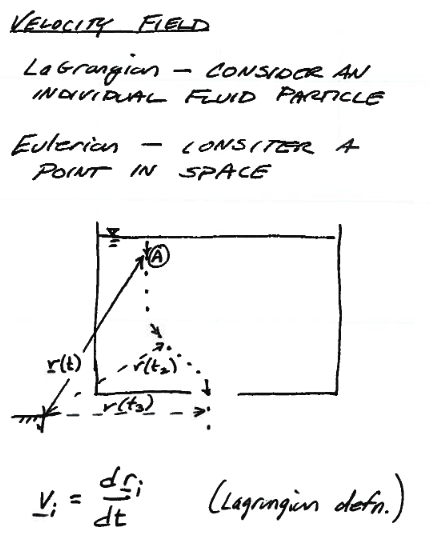
Coordinate systems for velocity description¶
Field is from the mathematical description of a field. Various rules apply to fields, and these are used later on.
Magnetic Fields
Elactric Fields
Gravitational Fields
Strawberry Fields (forever)
Are examples of “things” that are fields. The idea is that if you know location, you know behavior.

Parametric (in time) velocity field equation¶
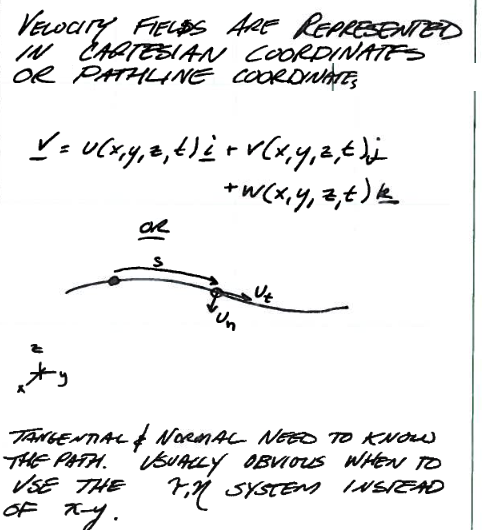
Streamline coordinates for a velocity¶
Uniform Flow¶
Uniform flow occurs in things with relatively straight pathlines (streamlines), and constant cross section geometries. Things like pipes, channels of constant geometry, aquifers (like sand-filled pipes), and petroleum reservoirs (like aquifers, but with hydrocarbons in economically useable amounts).
If geometry changes like in a nozzle, then non-uniform flow. If at steady flowrate, non-uniform can have convective acceleration.

Uniform flow examples¶
Laminar flow is where fluid in adjacent layers (think back to definition of viscosity) move smoothly with respect to each other (very little mixing across layers). Turbulent flow has layers mixing substantially.
Viscous shear stresses impact the flow.
Inviscid shear stresses small enough to ignore.
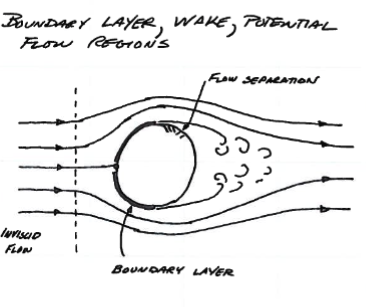
Multiple flow regimes around a cylinder¶
Different regimes can exist simultaneously in adjacent space as in boundary6-1. The approach region is nearly inviscid, at the boundary viscid flow along the interface, separation where flow leaves the interface, and a wake region. Drag increases where there is separation - prevention is impossible but drag reduction by delaying sepaeration is possible.
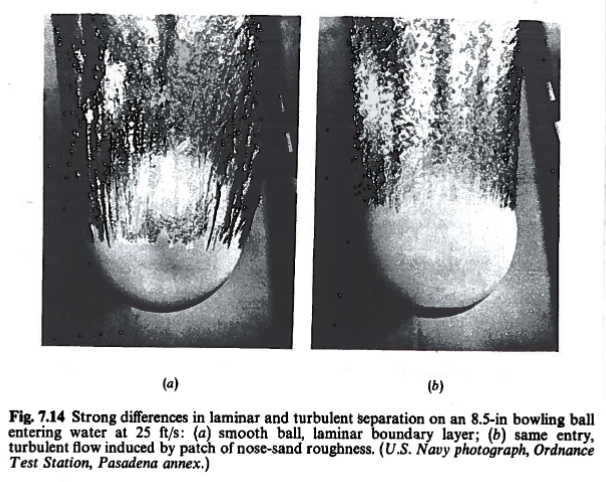
Surface modifications to delay separation¶
Acceleration occurs when there is a change in speed and/or direction.
Apply these ideas in multiple spatial dimensions:
Re-expressing using kinematics terms
Some tidying
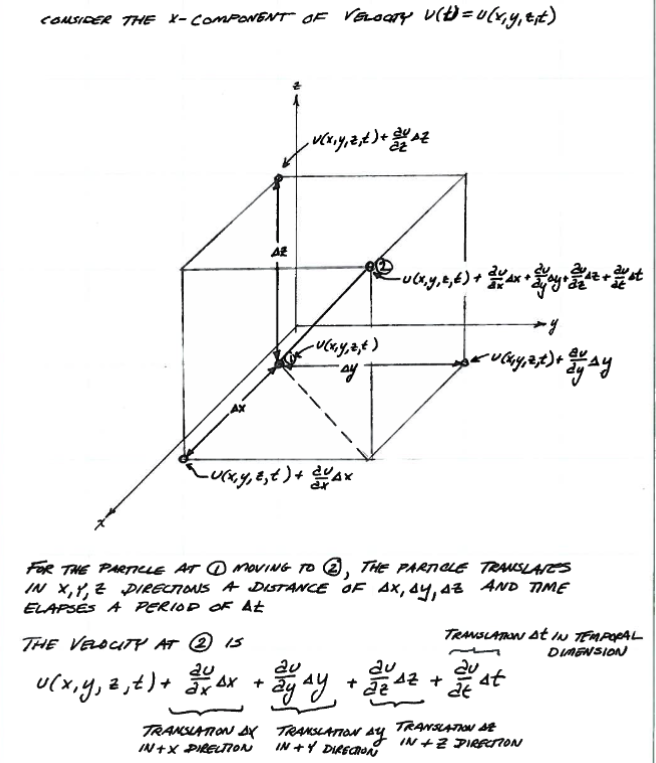
A schematic of particle motion over a short time interval.
We can examine the acceleration either as above or as:
Now recall the expression derived when we demonstrated that pressure should be scalar
Employ some of these ideas in an example.
Example: Flow field in a nozzle¶
Here is an example of the type of analysis involved. Identify the problem solving steps depicted.