Fluid Statics¶
Fluid statics deals with forces in fluids that are have no relative motion within the fluid. The vessel containing the fluid may be at non-zero velocity or acceleration, but the fluid body within the vessel has no relative motion.
Two principal types of forces involved are body and surface forces as shown in FluidStatics
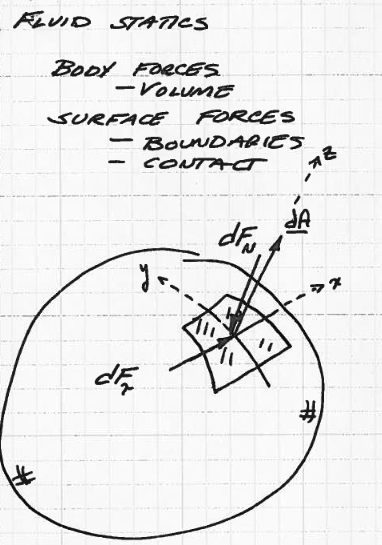
A sphere of some fluid, depicting a local coordinate system, differential area and a normal and tangential force pair¶
Body forces are developed without contact and are distributed over the entire volume of a fluid. In the sketch the weight of the sphere is a body force.
Surface forces act at boundaries of a medium through contant. The normal force in the sketch (which is the product of pressure and area) is a surface force, defined on the surface of the sphere.
Stress is the limiting value of \(\frac{dF}{dA}\); in the sketch there are two stresses: a normal stress (usually called pressure), and a tangential stress (usually called shear).
Shear stresses are formed by friction, no-slip assumption, and other practically occuring situations.
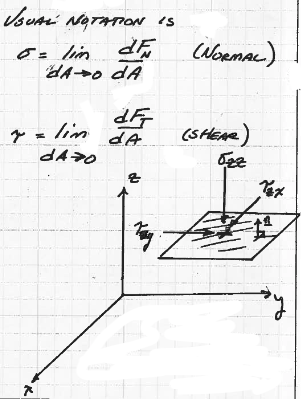
Shear and normal stresses on a plane parallel to x-y coordinate plane, at some value z.¶
Stresses is a diagram of a small planar element in a 3-D cartesian coordinate system that illustrate normal and shear stresses. The tensor-like naming system is also indicated.
A conventional notation is \(\sigma_{n,i-k}\) for normal stress, and \(\tau_{n,i-k}\) for shear stress. The first subscript is the direction of the outward pointing normal vector from the application plane (in the drawing +z), the second subscript is the direction of force application, with the normal stress positive into the plane. In the drawing the three stresses are \(\sigma_{z,z}\),\(\tau_{z,x}\), and \(\tau_{z,y}\).
