Example 2: Circuit Analysis¶
Suppose we wish to analyze the electric circuit in Fig. 2.
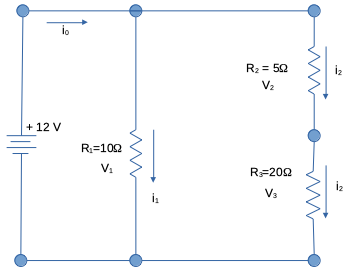
Fig. 2 Caption¶
Applying the problem solving protocol might be something like
Step 1: Problem Statement¶
Determine the unknown parameters that characterize the behavior of the circuit depicted in Fig. 2.
Step 2: Sketch the Situation¶
Done, we will refer to the figure as needed.
Step 3: List Known and Unknown Values¶
Known:
Circuit topology (configuration) and component relative locations.
Source voltage: +12 volts as shown on the diagram.
Resistor values: \(R_1=~10 \Omega\) , \(R_2=~5 \Omega\) , \(R_3=~20 \Omega\)
Unknown:
The current in different parts of the circuit: \(i_0\) , \(i_1\) , \(i_2\) .
The voltage drops (differences) across each resistor: \(V_1\) , \(V_2\) , \(V_3\) .
Step 4: Identify Governing Principles¶
Ohm’s law: The voltage drop across a resiostor is the product of current frowing through the resistor and the resistance; \(V=IR\) .
Kirchoff’s Law - Resistors in Series; \(R_T=R_1 + R_2 + \dots+ R_n\)
Kirchoff’s Law - Resistors in Parallel; \(R_T=\frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \dots+ \frac{1}{R_n}}\)
Step 5: Analysis¶
First observe the left leg of the circuit has a single resistor, and the voltage drop must be the total voltage applied, so its current value is \(i_1 = \frac{V_1}{R_1} = \frac{12}{10} = 1.2 \text{A}\)
The next leg has the same total voltage drop, but distributed by Kirkchoff’s law over the two resistors as \(i_2 = \frac{V_2+V_3}{R_2+R_3} = \frac{12}{25} = 0.48 \text{A} \)
The total current flow is the sum of the two legs \(i_0 = i_1+i_2 = 1.68 \text{A}\)
With the current known in the system we can solve for the individual voltage drops from Ohm’s law as:
\(V_1 = i_1 R_1 = 1.2\text{ A}*10.0~\Omega = 12.0 \text{ V}\)
\(V_2 = i_2 R_2 = 0.48\text{ A}*5.0~\Omega = 2.4 \text{ V}\)
\(V_3 = i_2 R_3 = 0.48\text{ A}*20.0~\Omega = 9.6 \text{ V}\)
Using the Jupyter Notebook as a Calculator¶
Below we repeat the analysis directly in a Notebook
def ohms_law_voltage(current,resistance):
ohms_law_voltage = current*resistance
return(ohms_law_voltage)
def ohms_law_current(voltage,resistance):
ohms_law_current = voltage/resistance
return(ohms_law_current)
emf = 12
resistance_1 = 10
resistance_2 = 5
resistance_3 = 20
print("Circuit Example Inputs")
print("\nTotal Supply Voltage ",emf," Volts")
print("Resistance 1 = ",resistance_1,"Ohms \nResistance 2 = ",resistance_2,"Ohms \nResistance 3 = ",resistance_3,"Ohms")
current_1 = ohms_law_current(emf,resistance_1)
current_2 = ohms_law_current(emf,resistance_2+resistance_3)
current_0 = current_1 + current_2
voltage_1 = ohms_law_voltage(current_1,resistance_1)
voltage_2 = ohms_law_voltage(current_2,resistance_2)
voltage_3 = ohms_law_voltage(current_2,resistance_3)
print("\nSolution to Circuit Example")
print("\nCurrent 0 = ",current_0,"Amperes \nCurrent 1 = ",current_1,"Amperes \nCurrent 2 = ",current_2,"Amperes ")
print("Voltage 1 = ",voltage_1,"Volts \nVoltage 2 = ",voltage_2,"Volts \nVoltage 3 = ",voltage_3,"Volts")
print("\nRedundancy Checks")
if (voltage_1)== emf:
print("\nVoltage 1 = Total Supply Voltage (Correct)")
else:
print("Error in redundancy checks")
if (voltage_2+voltage_3)== emf:
print("Voltage 2 + Voltage 3 = Total Supply Voltage (Correct)")
else:
print("Error in redundancy checks")
Circuit Example Inputs
Total Supply Voltage 12 Volts
Resistance 1 = 10 Ohms
Resistance 2 = 5 Ohms
Resistance 3 = 20 Ohms
Solution to Circuit Example
Current 0 = 1.68 Amperes
Current 1 = 1.2 Amperes
Current 2 = 0.48 Amperes
Voltage 1 = 12.0 Volts
Voltage 2 = 2.4 Volts
Voltage 3 = 9.6 Volts
Redundancy Checks
Voltage 1 = Total Supply Voltage (Correct)
Voltage 2 + Voltage 3 = Total Supply Voltage (Correct)
Step 6: Discussion¶
Observe some of the features of the notebook solution. Ohms’ law is represented as functions for code readability. The inputs are “echoed” to the output. The results are displayed and labeled including units (which we have to program into the script). A redundancy check is included, in this case because its simple to perform. A few newline characters are embedded to improve readability, but really its just our hand calculations performed in an orderly sequence.
The utility of the scripted solution is for doing “what-if” analysis. Suppose we later determine that \(R_2\) should be increased to \(10~\Omega\). With our programmed tool its quite easy to just change the input-
emf = 12
resistance_1 = 10
resistance_2 = 10 # changed from 5
resistance_3 = 20
print("Circuit Example Inputs")
print("\nTotal Supply Voltage ",emf," Volts")
print("Resistance 1 = ",resistance_1,"Ohms \nResistance 2 = ",resistance_2,"Ohms \nResistance 3 = ",resistance_3,"Ohms")
current_1 = ohms_law_current(emf,resistance_1)
current_2 = ohms_law_current(emf,resistance_2+resistance_3)
current_0 = current_1 + current_2
voltage_1 = ohms_law_voltage(current_1,resistance_1)
voltage_2 = ohms_law_voltage(current_2,resistance_2)
voltage_3 = ohms_law_voltage(current_2,resistance_3)
print("\nSolution to Circuit Example")
print("\nCurrent 0 = ",current_0,"Amperes \nCurrent 1 = ",current_1,"Amperes \nCurrent 2 = ",current_2,"Amperes ")
print("Voltage 1 = ",voltage_1,"Volts \nVoltage 2 = ",voltage_2,"Volts \nVoltage 3 = ",voltage_3,"Volts")
print("\nRedundancy Checks")
if (voltage_1)== emf:
print("\nVoltage 1 = Total Supply Voltage (Correct)")
else:
print("Error in redundancy checks")
if (voltage_2+voltage_3)== emf:
print("Voltage 2 + Voltage 3 = Total Supply Voltage (Correct)")
else:
print("Error in redundancy checks")
Circuit Example Inputs
Total Supply Voltage 12 Volts
Resistance 1 = 10 Ohms
Resistance 2 = 10 Ohms
Resistance 3 = 20 Ohms
Solution to Circuit Example
Current 0 = 1.6 Amperes
Current 1 = 1.2 Amperes
Current 2 = 0.4 Amperes
Voltage 1 = 12.0 Volts
Voltage 2 = 4.0 Volts
Voltage 3 = 8.0 Volts
Redundancy Checks
Voltage 1 = Total Supply Voltage (Correct)
Voltage 2 + Voltage 3 = Total Supply Voltage (Correct)
