Contents

Logistic Regression

Background

Multiple Variable Models

\[ \begin{align}\begin{aligned}Y_{obs} = \frac{e^{\bf{\beta}^TX}}{1 + e^{\bf{\beta}^TX}} + \epsilon$$<br>\\<!--$Y_{mod} = \frac{e^{\bf{\beta}^TX}}{1 + e^{\bf{\beta}^TX}}$<br>-->\\where\end{aligned}\end{align} \]

\begin{gather} \mathbf{\beta}= \begin{pmatrix} \beta_0 \ \beta_1 \ \vdots \ \beta_m \ \end{pmatrix} \end{gather} $$

\[\begin{split} \begin{gather} \mathbf{X}= \begin{pmatrix} 1 & x_{1,1} & x_{1,2}&\dots & x_{1,m}\\ 1 & x_{2,1} & x_{2,2}&\dots & x_{2,m}\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ 1 & x_{n,1} & x_{n,2}&\dots & x_{n,m}\\ \end{pmatrix} \end{gather} \end{split}\]

The matrix has as many rows as observations to fit, and as many columns as predictor variables.

Fitting Process

The logistic regression method attempts to find values of \(\beta\) that minimizes the log-likelihood function

\[log_e L(\beta) = Y_{obs}^T \cdot (\beta^TX) - log_e \bf{1}^T \cdot (1 + e^{{\beta}^TX})\]

The presence of the last term makes the process a search process (instead of a single equation to solve), some form of iterative least squares. In general we will rely on packages to handle this work - an example follows

Read the database

import pandas as pd
import numpy as np
import sklearn.metrics as metrics
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

mydatabase = pd.read_csv('LogisticRegressionHomebrewExample.csv')

Verify the read, and plot the database

mydatabase.describe()
X1 X2 Class
count 20000.000000 20000.000000 20000.000000
mean 0.496920 2.001764 0.500000
std 1.113666 2.240266 0.500013
min -4.214002 -3.489115 0.000000
25% -0.260873 -0.015846 0.000000
50% 0.498444 1.978725 0.500000
75% 1.264066 4.016432 1.000000
max 4.605613 7.945987 1.000000 
#Split dataframe based on class value and plot
classone = mydatabase[mydatabase['Class']<1.0]
classzero = mydatabase[mydatabase['Class']>0.0]
# plot the two classes as red and blue
plt.figure(figsize=(10, 8))
plt.scatter(classzero['X1'],classzero['X2'], c="red", alpha=0.3)
plt.scatter(classone['X1'],classone['X2'], c="blue", alpha=0.3)
plt.legend(["Class 0","Class 1"])
plt.xlabel('X1 Predictor') 
plt.ylabel('X2 Predictor') 
plt.grid(which='both')
plt.show()
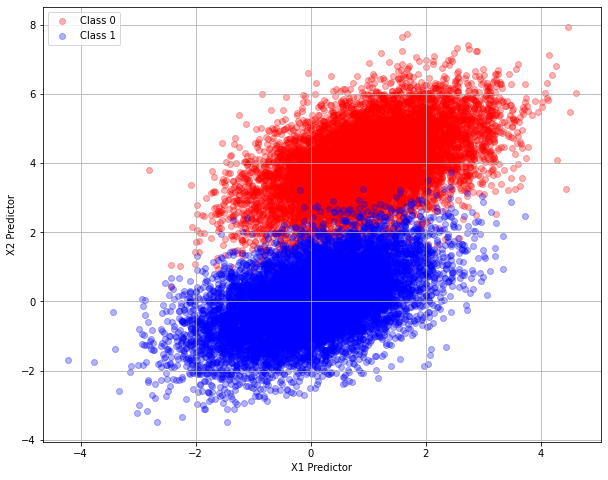
../../_images/1topic_6_0.png

The two classes appear different enough so the logistic-regression classification seems possible. For example if the predictor input is \([0,0]\) then the class is likely “Class 1”, whereas if the predictor input is \([0,4]\) then the class is likely “Class 0” according to the above plot.

#split dataset in features and target variable
feature_cols = ['X1', 'X2']
X = mydatabase[feature_cols] # Features
y = mydatabase["Class"] # Target variable

# split X and y into training and testing sets
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)

# import the class
from sklearn.linear_model import LogisticRegression

# instantiate the model (using the default parameters)
#logreg = LogisticRegression()
logreg = LogisticRegression()
# fit the model with data
logreg.fit(X_train,y_train)

#
y_pred=logreg.predict(X_test)

# import the metrics class
from sklearn import metrics
cnf_matrix = metrics.confusion_matrix(y_pred, y_test)
cnf_matrix

array([[2435,   58],
       [  42, 2465]])

class_names=[0,1] # name  of classes
fig, ax = plt.subplots()
tick_marks = np.arange(len(class_names))
plt.xticks(tick_marks, class_names)
plt.yticks(tick_marks, class_names)
# create heatmap
sns.heatmap(pd.DataFrame(cnf_matrix), annot=True, cmap="YlGnBu" ,fmt='g')
ax.xaxis.set_label_position("top")
plt.tight_layout()
plt.title('Confusion matrix', y=1.1)
plt.ylabel('Predicted label')
plt.xlabel('Actual label');
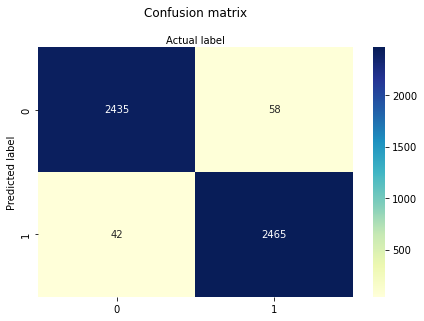
../../_images/1topic_12_0.png

Now lets build a classification (class prediction) engine using logistic regression results.

First we need the sigmoid response function where

\[sigmoid(X,\beta) = 1 + e^{{\beta}^TX} \]
def sigmoid(scores): # scores = b0+b1X1+b2X2+... where b0,b1,b2,... are specified
    return 1/(1+np.exp(-scores))

Now lets use our two obvious values from the discussion above

inputs = np.array([[0],[1]]) # one example input, should evaluate as
scores = np.dot(logreg.coef_,inputs) + logreg.intercept_
estimated_class = sigmoid(np.dot(logreg.coef_,inputs) + logreg.intercept_)[0,0] # grab the only element
print("X1 Input = ",inputs[0][0],"\nX2 Input = ",inputs[1][0],"\nEstimated Class Value",round(estimated_class,0))

X1 Input =  0 
X2 Input =  1 
Estimated Class Value 0.0

inputs = np.array([[0],[4]]) # one example input, should evaluate as
scores = np.dot(logreg.coef_,inputs) + logreg.intercept_
estimated_class = sigmoid(np.dot(logreg.coef_,inputs) + logreg.intercept_)[0,0] # grab the only element
print("X1 Input = ",inputs[0][0],"\nX2 Input = ",inputs[1][0],"\nEstimated Class Value",round(estimated_class,0))

X1 Input =  0 
X2 Input =  4 
Estimated Class Value 1.0

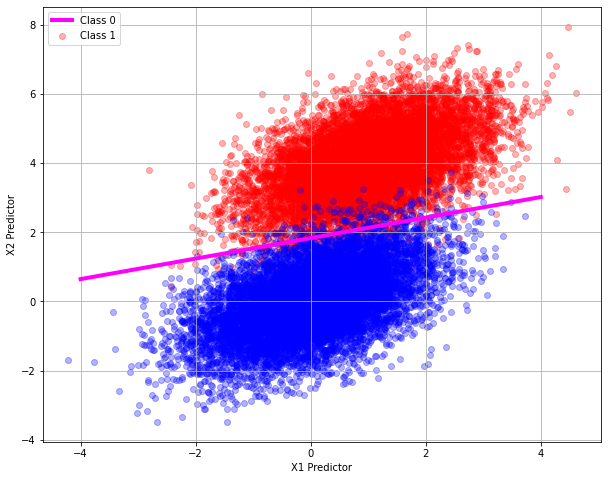
So now we have a classifer function, we could probably draw a dividing line back on the original plot and identify the dividing line, we only need two points where the classifier returns a value of 0.5 as below

inputs = np.array([[-4],[0.645]]) # one example input, should evaluate as
scores = np.dot(logreg.coef_,inputs) + logreg.intercept_
estimated_class = sigmoid(np.dot(logreg.coef_,inputs) + logreg.intercept_)[0,0] # grab the only element
print("X1 Input = ",inputs[0][0],"\nX2 Input = ",inputs[1][0],"\nEstimated Class Value",round(estimated_class,3))

X1 Input =  -4.0 
X2 Input =  0.645 
Estimated Class Value 0.502

inputs = np.array([[4],[3.018]]) # one example input, should evaluate as
scores = np.dot(logreg.coef_,inputs) + logreg.intercept_
estimated_class = sigmoid(np.dot(logreg.coef_,inputs) + logreg.intercept_)[0,0] # grab the only element
print("X1 Input = ",inputs[0][0],"\nX2 Input = ",inputs[1][0],"\nEstimated Class Value",round(estimated_class,3))

X1 Input =  4.0 
X2 Input =  3.018 
Estimated Class Value 0.5

Our two points by trial and error are: \([-4.0,0.645]\) and \([4.0,3.018]\) we can add this line to our plot

# plot the two classes as red and blue
plt.figure(figsize=(10, 8))
plt.scatter(classzero['X1'],classzero['X2'], c="red", alpha=0.3)
plt.scatter(classone['X1'],classone['X2'], c="blue", alpha=0.3)
plt.plot([-4,4],[0.645,3.018],c="magenta",linewidth=4)
plt.legend(["Class 0","Class 1"])
plt.xlabel('X1 Predictor') 
plt.ylabel('X2 Predictor') 
plt.grid(which='both')
plt.show()
../../_images/1topic_22_0.png

Single Variable Models

A single variable model is a special case of the multi-variate approach with the following modifications:

\[\begin{split} \begin{gather} \mathbf{\beta}= \begin{pmatrix} \beta_0 \\ \beta_1 \\ \end{pmatrix} \end{gather} \end{split}\]
\[\begin{split} \begin{gather} \mathbf{X}= \begin{pmatrix} 1 & x_{1,1} \\ 1 & x_{2,1} \\ \vdots & \vdots \\ 1 & x_{n,1} \\ \end{pmatrix} \end{gather} \end{split}\]

A simple example follows:

toxicity = pd.DataFrame([[1,2,3,4,5,6],[28,53,93,126,172,197]],["Log_Dose","Deaths"] )
toxicity = toxicity.transpose()
toxicity.head()
# compute death fraction, all doses exposed to 250 subjects
toxicity["Fraction"]=toxicity["Deaths"]/250.0
# declare lethal id fraction >0.5

def islethal(value):
    if value >= 0.5:
        islethal = 1
    else:
        islethal = 0
    return(islethal)

toxicity["Class"]=toxicity["Fraction"].apply(islethal)
toxicity.head()
Log_Dose Deaths Fraction Class
0 1 28 0.112 0
1 2 53 0.212 0
2 3 93 0.372 0
3 4 126 0.504 1
4 5 172 0.688 1 
def log_likelihood(features, target, weights): # features are the design variables; weights are the b0,b1,b2,...;target is the known class (0 or 1)
    scores = np.dot(features, weights)  
    ll = np.sum(target * scores - np.log(1 + np.exp(scores)))  
    return ll

def logistic_regression(features, target, num_steps, learning_rate, add_intercept=False, verbose=True, exit_tolerance = 1.0e-9):
    if add_intercept: 
        intercept = np.ones((features.shape[0], 1))  
        features = np.hstack((intercept, features))     
# print statements are for debugging        
    weights = np.zeros(features.shape[1])  # not sure about this line
    print("initial weights = ",weights)
    print("initial log likelihood = ",log_likelihood(features, target, weights))
    
#          
    for step in range(num_steps): 
        llold = log_likelihood(features, target, weights)
        if verbose: print("start weights = ",weights) 
        scores = np.dot(features, weights) 
        if verbose: print("start scores = ",scores)
        predictions = sigmoid(scores)  
        if verbose: print("predictions = ",predictions)
        output_error_signal = target - predictions      
        gradient = np.dot(features.T, output_error_signal)    
        weights = weights + learning_rate * gradient 
        if verbose: print("new weights = ",weights)
        newscores = np.dot(features, weights) 
        if verbose: print("new scores = ",newscores)
        llnew = log_likelihood(features, target, weights)

# test for exit
        if abs(llnew-llold) <= exit_tolerance:
            print("Exit Tolerance Satisfied \n  LL is not changing")
            print("step = ",step) 
            print("ll = ",log_likelihood(features, target, weights))
            break # exit the loop
        if step % 5 == 0:      
            if verbose: print("step = ",step) 
            if verbose: print("ll = ",log_likelihood(features, target, weights))
            if verbose: print("error signal = ",output_error_signal)
            if verbose: print("predictions = ",predictions)
# print on exit
    print("step = ",step) 
    print("ll = ",log_likelihood(features, target, weights))
    print("error signal = ",output_error_signal)
    print("predictions = ",predictions)
    return weights

Produce a design matrix using numpy and the dataframe we read. Similarily the class vector (of 0’s and 1’s) is constructed from the dataframe. These new objects have row-wise correspondence; that is a row of designmatrix corresponds to the same row of classvector. In terms of the above expressions

$\(\text{classvector} = Y_{obs} \)$

$\(\text{designmatrix} = X\)$

designmatrix = mydatabase[["X1","X2"]].to_numpy()
classvector = mydatabase["Class"].to_numpy()

These are supplied to our regression machine

betas = logistic_regression(designmatrix, classvector, 900, 0.00001, add_intercept=False, verbose=False)

initial weights =  [0. 0.]
initial log likelihood =  -13862.943611198905

Exit Tolerance Satisfied 
  LL is not changing
step =  621
ll =  -8139.368262867247
step =  621
ll =  -8139.368262867247
error signal =  [-0.4258073  -0.69253714 -0.32390763 ...  0.04174041  0.01879931
  0.0332575 ]
predictions =  [0.4258073  0.69253714 0.32390763 ... 0.95825959 0.98120069 0.9667425 ]

modelvector = sigmoid(np.dot(designmatrix, betas))

# plot the two classes as red and blue
plt.figure(figsize=(10, 8))
plt.scatter(classvector,modelvector, c="red", alpha=0.3)
#plt.scatter(classone['X1'],classone['X2'], c="blue", alpha=0.3)
#plt.legend(["Class 0","Class 1"])
plt.xlabel('X1 Predictor') 
plt.ylabel('X2 Predictor') 
plt.grid(which='both')
plt.show()
../../_images/1topic_35_0.png 
modelvector[1]

0.6925371237744782

classvector[100]

0

sigmoid(np.dot([0,2], betas))

0.8509476740456239

sigmoid(np.dot([0,4], betas))

0.9702321502038639