Evaluating Integrals¶
Background¶
Numerical integration is the numerical approximation of
\(\begin{equation} I = \int_a^b f(x)dx \end{equation}\)
Consider the problem of determining the shaded area under the curve \(y = f(x)\) from \(x = a\) to \(x = b\), as depicted in the figure below, and suppose that analytical integration is not feasible.
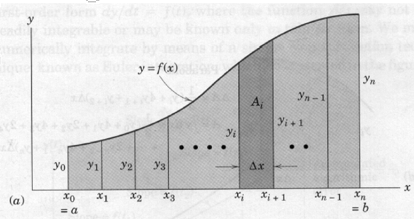
The function may be known in tabular form from experimental measurements or it may be known in an analytical form. The function is taken to be continuous within the interval \(a < x < b\). We may divide the area into \(n\) vertical panels, each of width \(\Delta x = (b - a)/n\), and then add the areas of all strips to obtain \(A~\approx \int ydx\).
A representative panel of area \(A_i\) is shown with darker shading in the figure. Three useful numerical approximations are listed in the following sections. The approximations differ in how the function is represented by the panels — in all cases the function is approximated by known polynomial models between the panel end points.
In each case the greater the number of strips, and correspondingly smaller value of \(\Delta x\), the more accurate the approximation. Typically, one can begin with a relatively small number of panels and increase the number until the resulting area approximation stops changing.
