F23 ES3 Solution Sketch#
LAST NAME, FIRST NAME
R00000000
Purpose :#
Apply selected analytical models for reactive transport
Assessment Criteria :#
Completion, results plausible, format correct, example calculations shown.
Problem 1 (Problem 6-7, pg. 588)#
An instantaneous release of biodegradable constituients occurs in a 1-D aquifer. Assume the mass released is \(1.0 ~kg\) over a \(10~m^2\) area normal to the flow direction, \(\alpha_l = 1.0~m\), the seepage velocity is 1.0 \(\frac{m}{day}\), and the half-life of the decaying constituient is 33 years.
Determine:
The maximum concentration at 100 meters from the source.
Plot a concentration history (annual intervals) for a 40 year period from release date for a location 100 meters from the source.
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
Known quantities#
initial mass = 1 kg.
cross section area = 10 \(m^2\)
\(\alpha_L = 1.0~m\)
\(v_x = 1~\frac{m}{d}\)
\(\lambda = \frac{t_{1/2}}{0.693}\)
list unknown quantities#
\(C(100,t)_{max}\)
Plot \(C(100,t)~\text{for}~t=1,2,...,40~yr\)
governing principles#
Finite mass implies instant release. Use equation 6.18 as modified on g. 175 in book
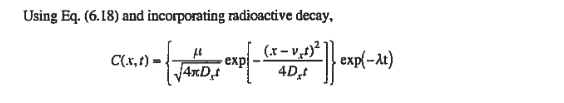
solution details (e.g. step-by-step computations)#
Build a prototype function
def c1addinst(distance,time,mass,dispersion,velocity,decay):
import math
term0 = math.exp(-1.0*decay*time)
term1 = math.sqrt(4.0*math.pi*dispersion*time)
term2 = math.exp(-((distance-velocity*time)**2)/(4.0*dispersion*time))
c1addinst = term0*(mass/term1)*term2
return(c1addinst)
Build input data manager, report intermediate computations
import math
total_mass = 1.0
area = 10
mass = total_mass/area
velocity = 1.0 #m/day
dispersivity = 1.0 #m
dispersion = velocity*dispersivity #m^2/day
half_life = 33 #years
decay = math.log(2)/(half_life)/365 #1/days
print("Mass : ",round(mass,3)," kg/m^3")
print("Decay constant : ",round(decay,6)," day^-1 ")
print("Dispersion : ",round(dispersion,3)," m^2/day")
#print(math.log(2))
Mass : 0.1 kg/m^3
Decay constant : 5.8e-05 day^-1
Dispersion : 1.0 m^2/day
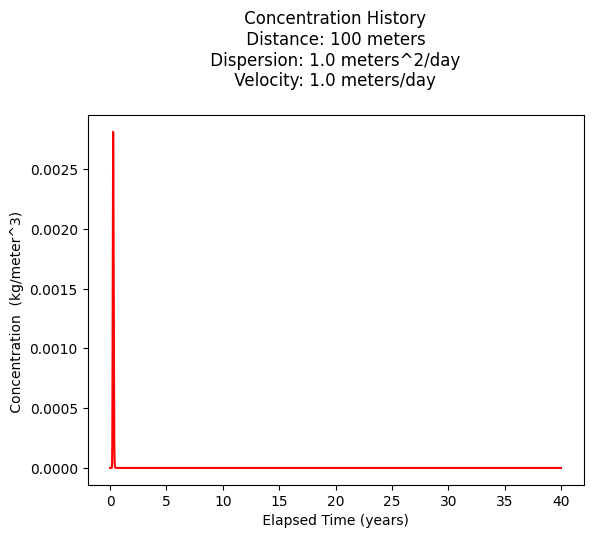
Plot a concentration history over 40 years
deltat = (1.0) #days
howmany = 365*40/deltat
howmany = int(howmany)
t = [] #days
for i in range(howmany):
t.append(float(i)*deltat)
if t[i] == 0: # trap zero time to prevent divide by zero
t[i]= 0.00000001
distance = 100 #years as days
c = [0 for i in range(howmany)] #concentration
for i in range(howmany):
c[i]=c1addinst(distance,t[i],mass,dispersion,velocity,decay)
# rescale time into years
for i in range(howmany):
t[i]=t[i]/365.
#
# Import graphics routines for picture making
#
from matplotlib import pyplot as plt
#
# Build and Render the Plot
#
plt.plot(t,c, color='red', linestyle = 'solid') # make the plot object
plt.title(" Concentration History \n Distance: " + repr(distance) + " meters \n" + " Dispersion: " + repr(dispersion) + " meters^2/day \n" + " Velocity: " + repr(velocity) + " meters/day \n") # caption the plot object
plt.xlabel(" Elapsed Time (years) ") # label x-axis
plt.ylabel(" Concentration (kg/meter^3) ") # label y-axis
#plt.plot([365,365],[0,c0])
#plt.plot([365*2,365*2],[0,c0])
#plt.text(365,100," year 1")
#plt.text(365*2,100," year 2")
#plt.savefig("ogatabanksplot.png") # optional generates just a plot for embedding into a report
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
#sys.exit() # used to elegant exit for CGI-BIN use
#print("Center of Distribution Position : ",round(time*velocity,2)," length units")
Plot a concentration history over one year (easier to see)
deltat = (1.0) #days
howmany = 365*1/deltat
howmany = int(howmany)
t = [] #days
for i in range(howmany):
t.append(float(i)*deltat)
if t[i] == 0: # trap zero time to prevent divide by zero
t[i]= 0.00000001
distance = 100 #years as days
c = [0 for i in range(howmany)] #concentration
for i in range(howmany):
c[i]=c1addinst(distance,t[i],mass,dispersion,velocity,decay)
# rescale time into years
for i in range(howmany):
t[i]=t[i]/365.
#
# Import graphics routines for picture making
#
from matplotlib import pyplot as plt
#
# Build and Render the Plot
#
plt.plot(t,c, color='red', linestyle = 'solid') # make the plot object
plt.title(" Concentration History \n Distance: " + repr(distance) + " meters \n" + " Dispersion: " + repr(dispersion) + " meters^2/day \n" + " Velocity: " + repr(velocity) + " meters/day \n") # caption the plot object
plt.xlabel(" Elapsed Time (years) ") # label x-axis
plt.ylabel(" Concentration (kg/meter^3) ") # label y-axis
#plt.plot([365,365],[0,c0])
#plt.plot([365*2,365*2],[0,c0])
#plt.text(365,100," year 1")
#plt.text(365*2,100," year 2")
#plt.savefig("ogatabanksplot.png") # optional generates just a plot for embedding into a report
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
#sys.exit() # used to elegant exit for CGI-BIN use
#print("Center of Distribution Position : ",round(time*velocity,2)," length units")
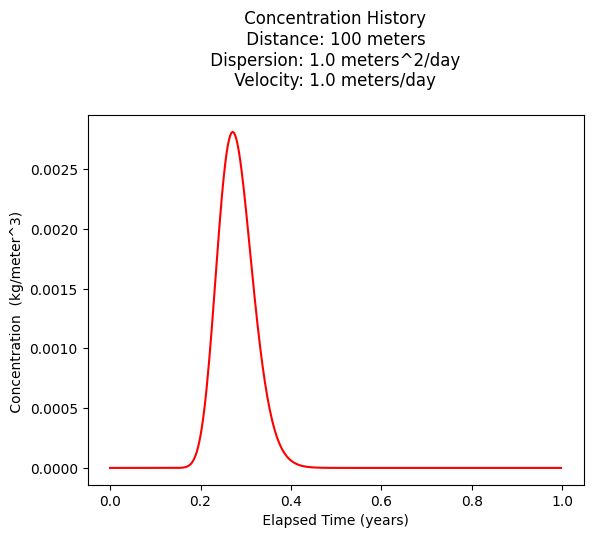
Looks like maximum occurs at about 100 days, but lets just be stupid about it and find the value from the plot, and report the time of occurance (in days)
print("Maximum concentration : ",max(c)," kg/m^3")
print(" Observed at : ",t[c.index(max(c))]*365," days")
print(c1addinst(distance,100,mass,dispersion,velocity,decay))
Maximum concentration : 0.0028119432286784715 kg/m^3
Observed at : 99.0 days
0.0028047609791774213
Problem 2 (Problem 6-9, pg. 589)#
An unintentional discharge from a point source introduced \(10~kg\) of contaminant mass to an aquifer. The seepage velocity is \(0.1~\frac{ft}{day}\) in the \(+x\) direction. The longitudinal dispersion coefficient is \(D_x = 0.01 \frac{ft^2}{day}\) the transverse dispersion coefficients are \(D_y = D_z = 0.001 \frac{ft^2}{day}\).
Determine:
Calculate the maximum concentration at \(x=100~ft\) and \(t=5~years\).
Calculate the concentration at \((x,y,z,t) = (200~ft,5~ft,2~ft,5~years)\)
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
governing principles#
point source spill; use Equation 6.28 in book

solution details (e.g. step-by-step computations)#
Create a prototype function
def c3addinst(x,y,z,t,m,dx,dy,dz,v,lm):
# Baetsle 1969 model
import math
term0 = math.exp(-1.0*lm*t)
term1 = 8.0*math.sqrt(math.pi*dx*t*math.pi*dy*t*math.pi*dz*t)
term2 = math.exp(-((x-v*t)**2)/(4.0*dx*t) -((y)**2)/(4.0*dy*t) -((z)**2)/(4.0*dz*t))
c3addinst = term0*(mass/term1)*term2
return(c3addinst)
Build input data manager, report intermediate computations
mass = 10.0 #kg
velocity = 0.1 #ft/day
disp_x = 0.01 #ft^2/day
disp_y = 0.001 #ft^2/day
disp_z = 0.001 #ft^2/day
print(" Mass : ",round(mass,3)," kg/m^3")
print("Pore velocity : ",round(velocity,3)," ft/day")
print(" Dispersion x : ",round(disp_x,3)," ft^2/day")
print(" Dispersion y : ",round(disp_y,3)," ft^2/day")
print(" Dispersion z : ",round(disp_z,3)," ft^2/day")
Mass : 10.0 kg/m^3
Pore velocity : 0.1 ft/day
Dispersion x : 0.01 ft^2/day
Dispersion y : 0.001 ft^2/day
Dispersion z : 0.001 ft^2/day
Calculate the maximum concentration at \(x=100~ft\)
use a history plot
Calculate the maximum concentration at \(t=5~years\)
use a profile plot
deltat = (1.0) #days
howmany = 1500/deltat
howmany = int(howmany)
t = [] #days
for i in range(howmany):
t.append(float(i)*deltat)
if t[i] == 0: # trap zero time to prevent divide by zero
t[i]= 0.00000001
x = 100 #ft
y = 0
z = 0
c = [0 for i in range(howmany)] #concentration
for i in range(howmany):
c[i]=c3addinst(x,y,z,t[i],mass,disp_x,disp_y,disp_z,velocity,0)
#
# Import graphics routines for picture making
#
from matplotlib import pyplot as plt
#
# Build and Render the Plot
#
plt.plot(t,c, color='red', linestyle = 'solid') # make the plot object
plt.title(" Concentration History \n Distance: " + repr(x) + " feet \n" ) # caption the plot object
plt.xlabel(" Elapsed Time (days) ") # label x-axis
plt.ylabel(" Concentration (kg/ft^3) ") # label y-axis
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
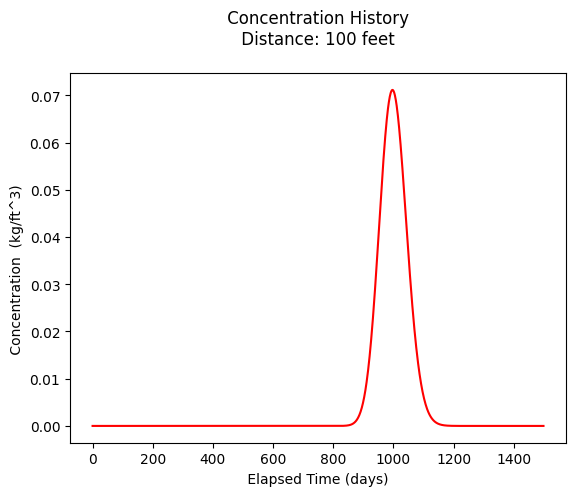
print("Maximum concentration : ",max(c)," kg/ft^3")
print(" Observed at : ",t[c.index(max(c))]," days")
Maximum concentration : 0.07114794548155023 kg/ft^3
Observed at : 997.0 days
deltax = (1.0) #days
howmany = 250/deltax
howmany = int(howmany)
x = [] #feet
for i in range(howmany):
x.append(float(i)*deltax)
t = 5*365 #days
y = 0
z = 0
c = [0 for i in range(howmany)] #concentration
for i in range(howmany):
c[i]=c3addinst(x[i],y,z,t,mass,disp_x,disp_y,disp_z,velocity,0)
#
# Import graphics routines for picture making
#
from matplotlib import pyplot as plt
#
# Build and Render the Plot
#
plt.plot(x,c, color='red', linestyle = 'solid') # make the plot object
plt.title(" Concentration Profile \n Time: " + repr(t) + " days \n" ) # caption the plot object
plt.xlabel(" Distance (feet) ") # label x-axis
plt.ylabel(" Concentration (kg/ft^3) ") # label y-axis
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
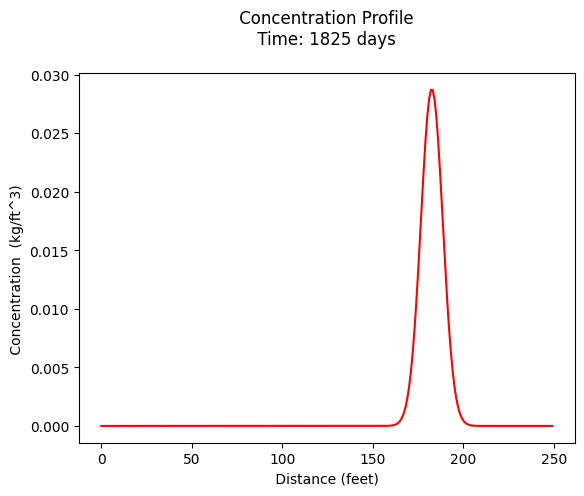
print("Maximum concentration : ",max(c)," kg/ft^3")
print(" Observed at : ",x[c.index(max(c))]," feet")
Maximum concentration : 0.02869482568927895 kg/ft^3
Observed at : 182.0 feet
Calculate the concentration at \((x,y,z,t) = (200~ft,5~ft,2~ft,5~years)\)
conc = c3addinst(200,5,2,5*365,mass,disp_x,disp_y,disp_z,velocity,0)
print("C(200,5,2,5) : ",round(conc,7)," kg/ft^3")
C(200,5,2,5) : 8.2e-06 kg/ft^3
Problem 3 (Problem 6-10, pg. 589)#
Apply the Domenico and Schwartz (1998) planar source model (pg. XXX) to a case of a continuous source that has been leaking contaminant into an aquifer for 15 years. The source had a width \(Y=6~m\) and depth \(Z=6~m\). The source concentration is \(10~\frac{mg}{l}\). The seepage velocity is \(0.057~\frac{m}{day}\). The longitudinal, transverse, and vertical dispervities are \(1~m\),\(0.1~m\), and \(0.01~m\) respectively.
Determine:
The contaminant concentration history at a location \(x=200~m\) from the source using 1-year increments for 30 years.
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
sketch(s)#
list known quantities#
list unknown quantities#
governing principles#
Using the planar source model (Eqn 6.31)
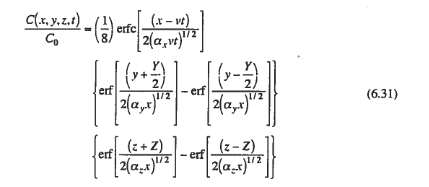
solution details (e.g. step-by-step computations)#
Usual procedure, first a prototype function - unlike prior cases will use dispersivities rather than dispersion coefficients:
def c3dad(conc0, distx, disty, distz, lenX, lenY, lenZ, dispx, dispy, dispz, velocity, etime):
import math
from scipy.special import erf, erfc # scipy needs to already be loaded into the kernel
# Constant of integration
term1 = conc0 / 8.0
# Centerline axis solution
arg1 = (distx - velocity*etime) / (2*math.sqrt(dispx*velocity*etime)) #dispx is dispersivity
term2 = erfc(arg1)
# Off-axis solution, Y direction
# arg2 = 2.0 * math.sqrt(dispy*distx / velocity)
arg2 = 2.0 * math.sqrt(dispy*distx) #dispy is dispersivity
arg3 = disty + 0.5*lenY
arg4 = disty - 0.5*lenY
term3 = erf(arg3 / arg2) - erf(arg4 / arg2)
# Off-axis solution, Z direction
# arg5 = 2.0 * math.sqrt(dispz*distx / velocity)
arg5 = 2.0 * math.sqrt(dispz*distx) #dispz is dispersivity
arg6 = distz + 0.5*lenZ
arg7 = distz - 0.5*lenZ
term4 = erf(arg6 / arg5) - erf(arg7 / arg5)
# Convolve the solutions
c3dad = term1 * term2 * term3 * term4
return c3dad
Now an input manager section
# inputs
conco = 10.0
velocity = 0.057
dispersivity_x = 1.0
dispersivity_y = 0.1
dispersivity_z = 0.01
width_y = 6.0
width_z = 6.0
xloc = 200.0
yloc = 0.0 # not explicit in problem statement
zloc = 0.0
time = 30*365 #years as days
# echo inputs
print("Source Concentration : ",round(conco,3)," ppm ")
print(" Velocity : ",round(velocity,3)," m/sec ")
print(" Dispersivity_x : ",round(dispersivity_x,3)," m ")
print(" Dispersivity_y : ",round(dispersivity_x,3)," m ")
print(" Dispersivity_z : ",round(dispersivity_x,3)," m ")
print(" Width Y : ",round(width_y,3)," m ")
print(" Width Z : ",round(width_z,3)," m ")
Source Concentration : 10.0 ppm
Velocity : 0.057 m/sec
Dispersivity_x : 1.0 m
Dispersivity_y : 1.0 m
Dispersivity_z : 1.0 m
Width Y : 6.0 m
Width Z : 6.0 m
Now build script for concentration history (time is the variable)
#
# forward define and initialize vectors for a profile plot
#
how_many_points = 30
deltat = time/how_many_points
t = [i*deltat for i in range(how_many_points)] # constructor notation
c = [0.0 for i in range(how_many_points)] # constructor notation
t[0]=1e-5 #cannot have zero time, so use really small value first position in list
#
# build the profile predictions
#
for i in range(0,how_many_points,1):
c[i] = c3dad(conco, xloc, yloc, zloc, 0, width_y, width_z, dispersivity_x, dispersivity_y, dispersivity_z, velocity, t[i])
for i in range(0,how_many_points,1):
t[i]=t[i]/365 # days as years
#
# Import graphics routines for picture making
#
from matplotlib import pyplot as plt
#
# Build and Render the Plot
#
plt.plot(t,c, color='red', linestyle = 'solid') # make the plot object
plt.title(" Concentration History \n ") # caption the plot object
plt.xlabel(" Time since release (years)") # label x-axis
plt.ylabel(" Concentration (ppm) ") # label y-axis
#plt.savefig("ogatabanksplot.png") # optional generates just a plot for embedding into a report
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
#sys.exit() # used to elegant exit for CGI-BIN use
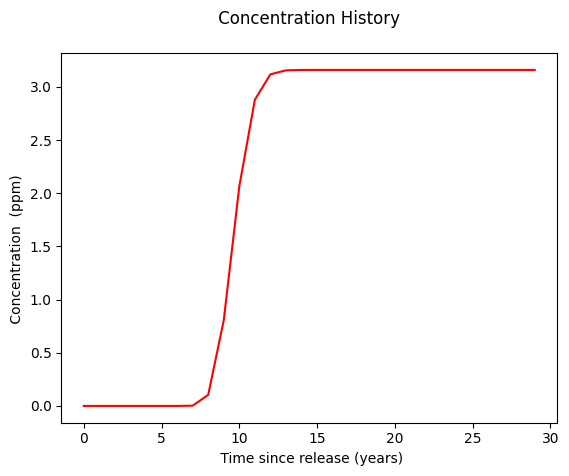
discussion#
The equilibrium concentration can be found from the plot either by finding the maximum in the list or just taking the last element in the list.
print("Equilibrium concentration @ x=200,y=0,z=0,t->big : ",round(max(c),3)," ppm ")
Equilibrium concentration @ x=200,y=0,z=0,t->big : 3.16 ppm
Problem 4#
The following table has data from a column test with bromide (conservative) and chromium (sorbed). The porosity of the soil was 0.485, the bulk density was 1.85 g/cc, velocity was 0.244 cm/min, and the column was 25.4 cm long with a diameter of 2.54 cm.
Time (min) |
Bromide \(\frac{C}{Co}\) |
Chromium \(\frac{C}{Co}\) |
|---|---|---|
0 |
0.000 |
0.000 |
15 |
0.000 |
0.000 |
30 |
0.005 |
0.000 |
45 |
0.003 |
0.000 |
60 |
0.013 |
0.000 |
75 |
0.075 |
0.000 |
90 |
0.137 |
0.000 |
105 |
0.530 |
0.000 |
120 |
0.841 |
0.000 |
135 |
1.000 |
0.000 |
150 |
1.000 |
0.000 |
165 |
1.000 |
0.009 |
180 |
1.000 |
0.186 |
195 |
1.000 |
0.595 |
210 |
1.000 |
0.791 |
225 |
1.000 |
0.875 |
240 |
1.000 |
0.913 |
255 |
1.000 |
0.946 |
270 |
1.000 |
0.946 |
285 |
1.000 |
1.000 |
300 |
1.000 |
1.000 |
315 |
1.000 |
1.000 |
330 |
1.000 |
1.000 |
345 |
1.000 |
1.000 |
360 |
1.000 |
1.000 |
Determine:
The dispersivity in cm
The retardation coefficient for \(Cr\).
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
solution details (e.g. step-by-step computations)#
Prototype function from class notes
#
# prototype decaying species function
#
def c1dadrd(c_source,space,time,dispersion,velocity,retardation,decay):
from math import sqrt,erf,erfc,exp # get special math functions
dee = dispersion/retardation
vee = velocity/retardation
uuu = (vee**2 + 4.0*decay*dee)
uuu = sqrt(uuu)
arg1 = (space*(vee-uuu))/(2.0*dee)
arg2 = (space - uuu*time)/(2.0*sqrt(dee*time))
arg3 = (space*(vee+uuu))/(2.0*dee)
arg4 = (space + uuu*time)/(2.0*sqrt(dee*time))
temp1 = c_source/2.0
temp2 = exp(arg1)
temp3 = erfc(arg2)
temp4 = exp(arg3)
temp5 = erfc(arg4)
c1dadrd = temp1*(temp2*temp3+temp4*temp5)
return c1dadrd
copy the data from the table above#
cut-n-paste, then
insert delimiters
Parse into useable lists
# copy the data from the table above (cut-n-paste, then insert delimiters)
p4df = [[0 ,0.000 ,0.000],
[15 ,0.000 ,0.000],
[30 ,0.005 ,0.000],
[45 ,0.003 ,0.000],
[60 ,0.013 ,0.000],
[75 ,0.075 ,0.000],
[90 ,0.137 ,0.000],
[105 ,0.530 ,0.000],
[120 ,0.841 ,0.000],
[135 ,1.000 ,0.000],
[150 ,1.000 ,0.000],
[165 ,1.000 ,0.009],
[180 ,1.000 ,0.186],
[195 ,1.000 ,0.595],
[210 ,1.000 ,0.791],
[225 ,1.000 ,0.875],
[240 ,1.000 ,0.913],
[255 ,1.000 ,0.946],
[270 ,1.000 ,0.946],
[285 ,1.000 ,1.000],
[300 ,1.000 ,1.000],
[315 ,1.000 ,1.000],
[330 ,1.000 ,1.000],
[345 ,1.000 ,1.000],
[360 ,1.000 ,1.000]]
# count rows
howmanyrows = len(p4df)
# allocate lists
t=[0 for i in range(howmanyrows)]
bromide=[0 for i in range(howmanyrows)]
chromium=[0 for i in range(howmanyrows)]
# parse into useful lists
for irow in range(howmanyrows):
t[irow]=p4df[irow][0]
bromide[irow]=p4df[irow][1]
chromium[irow]=p4df[irow][2]
if t[0]==0:t[0]=0.00001
build an input data manager
echo inputs
plot observations and model results
trial-and-error (or some optimization) to minimize prediction error by changing dispersivity and retardation to recover values
report results
# input data manager
porosity = 0.485
velocity = 0.244 #cm/min
dispersivity = 0.232 #initial guess - change to fit bromide curve
retardationBr = 1.0
retardationCr = 1.9
dCr = (1.2e-09)*60*100*100 #molecular diffusivity - in cm^2/min
dBr = (1.6e-04)*100*100/1440 #molecular diffusivity in cm^2/min
spdischarge = velocity*porosity
dispersion = dispersivity*velocity
length = 25.4 #cm
diameter = 2.54 #cm
rhob = 1.85 #g/ml
#echo inputs
print(" ---- Supplied Values ---- ")
print(" Porosity : ",porosity)
print(" Pore Velocity : ",round(velocity,3)," cm/min" )
print(" Dispersivity : ",dispersivity," cm ")
print(" Molecular Diffusivity Br : ",round(dBr,6)," cm^2/min ")
print(" Molecular Diffusivity Cr : ",round(dCr,6)," cm^2/min ")
print(" Retardation Factor Br : ",retardationBr)
print(" Retardation Factor Cr : ",retardationCr)
print(" ---- Computed Values ---- ")
print(" Specific Discharge : ",spdischarge," cm/min ")
print(" Dispersion : ",round(dispersion,3)," cm^2/min ")
print(" Kd-bromide : ",round((retardationBr-1)*(porosity/rhob),3))
print(" Kd-chromium : ",round((retardationCr-1)*(porosity/rhob),3))
# build simulation results
brmodel = [0 for i in range(howmanyrows)]
crmodel = [0 for i in range(howmanyrows)]
for irow in range(howmanyrows):
brmodel[irow]= c1dadrd(1.0,length,t[irow],dispersion+dBr,velocity,retardationBr,0)
crmodel[irow]= c1dadrd(1.0,length,t[irow],dispersion+dCr,velocity,retardationCr,0)
# compute some error measure
sseBr = 0.0
sseCr = 0.0
for irow in range(howmanyrows):
sseBr = sseBr + ((bromide[irow]-brmodel[irow])**2)
sseCr = sseCr + ((chromium[irow]-crmodel[irow])**2)
#plot simulation and observation results
from matplotlib import pyplot as plt
plt.plot(t,bromide, color='blue', linestyle = "none", marker = 'o') # make the plot object
plt.plot(t,chromium, color='orange', linestyle = "none", marker = 'o', fillstyle = 'none') # make the plot object
plt.plot(t,brmodel, color='blue', linestyle = "dotted" ) # make the plot object
plt.plot(t,crmodel, color='orange', linestyle = "dotted") # make the plot object
plt.title(" Concentration History \n " + " Bromide model SSE : " + repr(round(sseBr,5)) + "\n Chromium model SSE : " + repr(round(sseCr,5))) # caption the plot object
plt.xlabel(" Time since release (minutes)") # label x-axis
plt.ylabel(" C/Co ") # label y-axis
#plt.xscale('log')
#plt.yscale('log')
plt.legend(["Br-obs","Cr-obs","Br-mod","Cr-mod"])
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
#sys.exit() # used to elegant exit for CGI-BIN use
---- Supplied Values ----
Porosity : 0.485
Pore Velocity : 0.244 cm/min
Dispersivity : 0.232 cm
Molecular Diffusivity Br : 0.001111 cm^2/min
Molecular Diffusivity Cr : 0.00072 cm^2/min
Retardation Factor Br : 1.0
Retardation Factor Cr : 1.9
---- Computed Values ----
Specific Discharge : 0.11834 cm/min
Dispersion : 0.057 cm^2/min
Kd-bromide : 0.0
Kd-chromium : 0.236
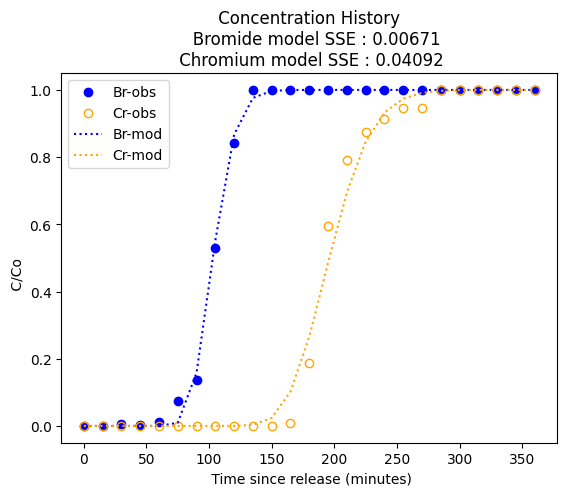
discussion#
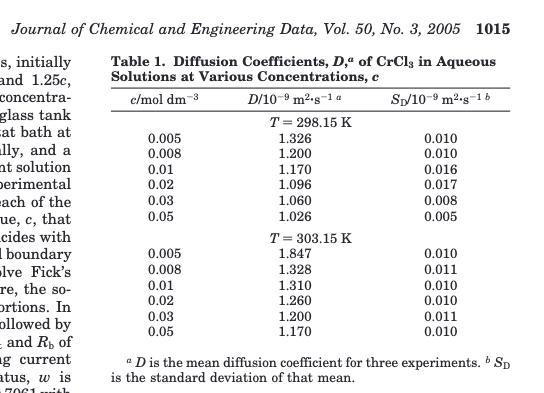
Trial-and-error fit could be replaced by an optimizer (Solver in excel, or some python equilivant), but hardly worth the effort - once you have the advection part (C/Co = 0.5) located, then dispersivity controls curvature. If one could argue for different dispersivities for each species could get a better fit, but dispersivtiy is considered a material property of the porous media. The solution above uses literature supplied diffusivities from:

and
Problem 5#
A batch isotherm test was performed with several 1-L solutions of the chemical of interest and one soil type, 20 g in each solution container. The initial and final solution concentrations are shown in the table. Fit the linear, Freundlich, and Langmuir isotherm equations to this data.
Initial Concentration (mg/L) |
Equilibrium Concentration (mg/L) |
|---|---|
7.10 |
6.71 |
4.53 |
4.18 |
1.89 |
1.63 |
1.31 |
1.10 |
1.03 |
0.85 |
Determine:
The Linear isotherm equation for these data (i.e. fit the isotherm model to the data), plot the isotherm and data
The Freundlich isotherm equation for these data, plot the isotherm and data
The Langmuir isotherm equation for these data, plot the isotherm and data
Which isotherm model produces the best fit for these data?
Show calculations and identify all fitted parameter values.
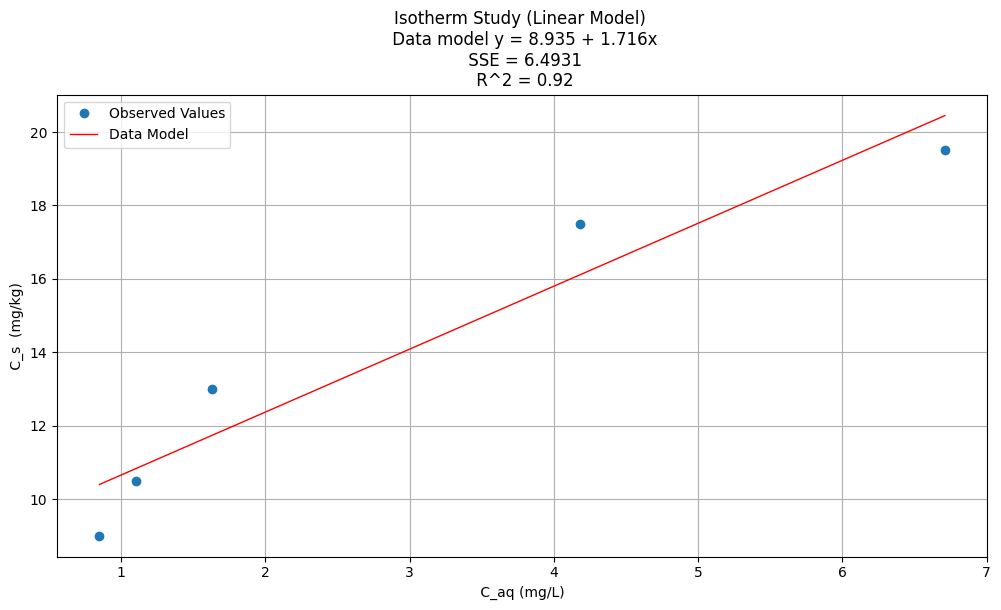
Linear isotherm#
Linear isotherm equation for these data (i.e. fit the isotherm model to the data), plot the isotherm and data
p5df = [[7.10 ,6.71],
[4.53 ,4.18],
[1.89 ,1.63],
[1.31 ,1.10],
[1.03 ,0.85]]
howmanyrows = len(p5df)# allocate lists
c0=[0 for i in range(howmanyrows)]
cEq=[0 for i in range(howmanyrows)]
cS=[0 for i in range(howmanyrows)]
cSoS=[0 for i in range(howmanyrows)]
#input values
massS = 0.020 #kg
volL = 1 #L
# build lists
for i in range(howmanyrows):
c0[i]=p5df[i][0]
cEq[i]=p5df[i][1]
cS[i]=(c0[i]-cEq[i])*volL/massS
cSoS[i]=cEq[i]/cS[i]
# Now we need to do some analysis to earn our keep
# heres how to do the fits using python
#Load the necessary packages
import numpy as np
import pandas as pd
import statistics
import statsmodels.formula.api as smf # here is the regression package to fit lines
data = pd.DataFrame({'X':cEq, 'Y':cS}) # we use X,Y as column names for simplicity
#data.head()
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('Y ~ X', data=data) # model object constructor syntax
model = model.fit()
# Predict values
y_pred = model.predict()
beta0 = model.params[0] # the fitted intercept
beta1 = model.params[1]
sse = model.ssr
rsq = model.rsquared
titleline = "Isotherm Study (Linear Model) \n Data model y = " + str(round(beta0,3)) + " + " + str(round(beta1,3)) + "x" # put the model into the title
titleline = titleline + '\n SSE = ' + str(round(sse,4)) + '\n R^2 = ' + str(round(rsq,3))
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(data['X'], data['Y'], 'o') # scatter plot showing actual data
plt.plot(data['X'], y_pred, 'r', linewidth=1) # regression line
plt.xlabel(" C_aq (mg/L) ") # label x-axis
plt.ylabel(" C_s (mg/kg) ") # label y-axis
plt.legend(['Observed Values','Data Model'])
plt.title(titleline)
plt.grid(which="both")
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
#sys.exit() # used to elegant exit for CGI-BIN use
/tmp/ipykernel_25016/2865912900.py:8: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
beta0 = model.params[0] # the fitted intercept
/tmp/ipykernel_25016/2865912900.py:9: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
beta1 = model.params[1]
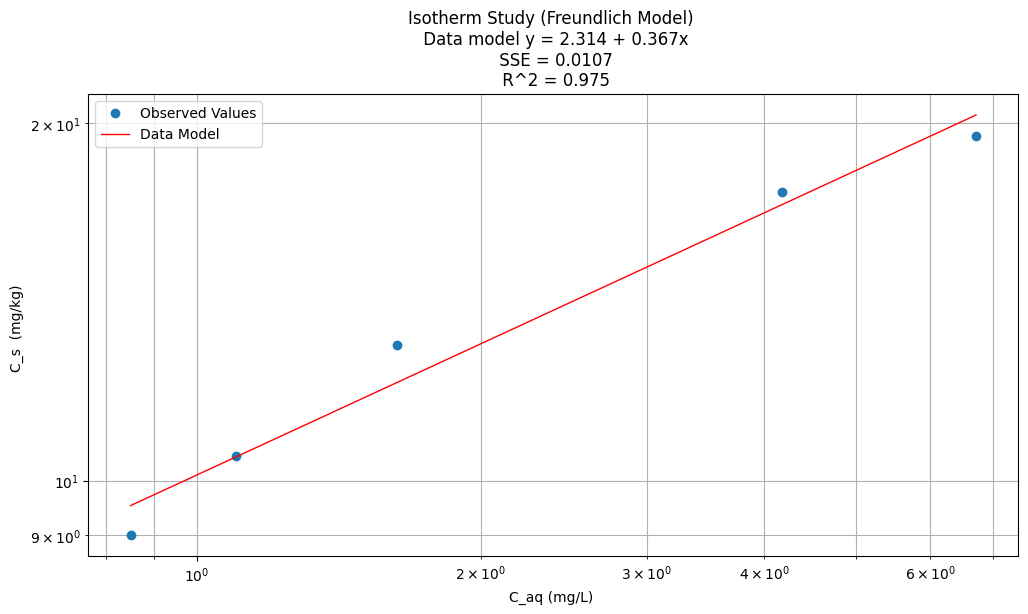
The Freundlich isotherm#
Apply Freundlich isotherm equation for these data, plot the isotherm and data
data = pd.DataFrame({'X':cEq, 'Y':cS}) # we use X,Y as column names for simplicity
import math
data['lnX']=data['X'].apply(math.log)
data['lnY']=data['Y'].apply(math.log)
#data.head()
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('lnY ~ lnX', data=data) # model object constructor syntax
model = model.fit()
# Predict values
y_pred = model.predict()
beta0 = model.params[0] # the fitted intercept
beta1 = model.params[1]
sse = model.ssr
rsq = model.rsquared
data['Ymod']=math.exp(beta0)*(data['X']**beta1)
print(data.head())
titleline = "Isotherm Study (Freundlich Model) \n Data model y = " + str(round(beta0,3)) + " + " + str(round(beta1,3)) + "x" # put the model into the title
titleline = titleline + '\n SSE = ' + str(round(sse,4)) + '\n R^2 = ' + str(round(rsq,3))
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(data['X'], data['Y'], 'o') # scatter plot showing actual data
plt.plot(data['X'],data['Ymod'], 'r', linewidth=1) # regression line
plt.xlabel("C_aq (mg/L) ") # label x-axis
plt.ylabel("C_s (mg/kg) ") # label y-axis
plt.yscale('log') # set y-axis to display a logarithmic scale #################
plt.xscale('log') # set x-axis to display a logarithmic scale #################
plt.legend(['Observed Values','Data Model'])
plt.title(titleline)
plt.grid(which="both")
plt.show() # plot to stdio -- has to be last call as it kills prior objects
/tmp/ipykernel_25016/2548014931.py:8: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
beta0 = model.params[0] # the fitted intercept
/tmp/ipykernel_25016/2548014931.py:9: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
beta1 = model.params[1]
X Y lnX lnY Ymod
0 6.71 19.5 1.903599 2.970414 20.324788
1 4.18 17.5 1.430311 2.862201 17.086669
2 1.63 13.0 0.488580 2.564949 12.097387
3 1.10 10.5 0.095310 2.351375 10.472862
4 0.85 9.0 -0.162519 2.197225 9.528125
The Langmuir isotherm#
Apply Langmuir isotherm equation for these data, plot the isotherm and data
data = pd.DataFrame({'X':cEq, 'Y':cSoS}) # we use X,Y as column names for simplicity
#data.head()
# Initialise and fit linear regression model using `statsmodels`
model = smf.ols('Y ~ X', data=data) # model object constructor syntax
model = model.fit()
# Predict values
y_pred = model.predict()
beta0 = model.params[0] # the fitted intercept
beta1 = model.params[1]
sse = model.ssr
rsq = model.rsquared
titleline = "Isotherm Study (Langmuir Model) \n Data model y = " + str(round(beta0,3)) + " + " + str(round(beta1,3)) + "x" # put the model into the title
titleline = titleline + '\n SSE = ' + str(round(sse,4)) + '\n R^2 = ' + str(round(rsq,3))
# Plot regression against actual data
plt.figure(figsize=(12, 6))
plt.plot(data['X'], data['Y'], 'o') # scatter plot showing actual data
plt.plot(data['X'], y_pred, 'r', linewidth=1) # regression line
plt.xlabel(" C_aq (mg/L) ") # label x-axis
plt.ylabel(" C_aq/C_s (mg/kg) ") # label y-axis
plt.legend(['Observed Values','Data Model'])
plt.title(titleline)
plt.grid(which="both")
plt.show() # plot to stdio -- has to be last call as it kills prior objects
plt.close('all') # needed when plt.show call not invoked, optional here
#sys.exit() # used to elegant exit for CGI-BIN use
/tmp/ipykernel_25016/1824087522.py:11: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
beta0 = model.params[0] # the fitted intercept
/tmp/ipykernel_25016/1824087522.py:12: FutureWarning: Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`
beta1 = model.params[1]
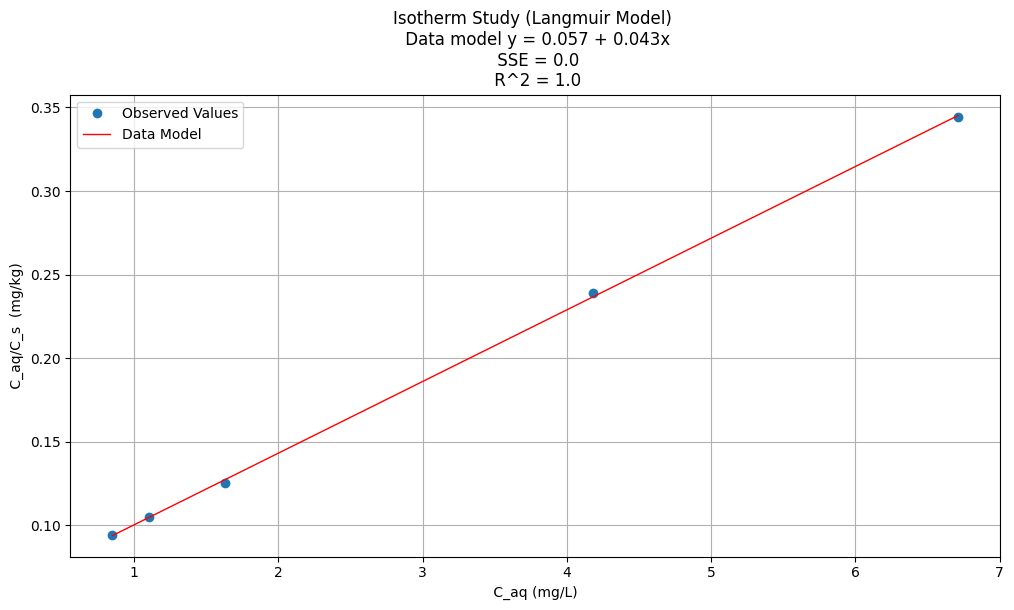
Which isotherm model produces the best fit for these data?#
Using R^2 as criterion,Langmuir is bestest