CE 5361 Surface Water Hydrology
Spring 2023 Exercise Set 2
LAST NAME, FIRST NAME
R00000000
Purpose :¶
Synthesize unit-hydrograph concepts from selected readings
Assessment Criteria :¶
Completion, plausible solution, documentation of methods employed.
Notes:¶
This exercise is largely a reading exercise, you will probably benefit from note taking during the readings - the "analysis" portion at the end is for you to self-asses your understanding and synthesis of the readings. You will apply what you read to construct a transfer function (excess P into Q) in Problem 2 then apply your function to a new storm (Problem 3).
Problem 1¶
Critically read in chronological order the following (these links access copies of cited articles):
- Sherman, L. (1932) “Stream Flow from Rainfall by the Unit Graph Method,” Engineering News Record, No. 108, pp. 501-505.
- Lienhard, J. H. (1964), A statistical mechanical prediction of the dimensionless unit hydrograph, J. Geophys. Res., 69(24), pp. 5231–5238
- Lienhard, John. (1972). Prediction of the dimensionless unit hydrograph. Nordic Hydrology. 3. pp. 107-109
- Dooge, JCI (1973) Linear theory of hydrologic systems. Tech. Bull. 1468, U.S. Dep. Agric., Agric. Res. Serv, Washington, D.C pp. 75-98
- Chow, V.T., Maidment,D.M., and Mays, L.W. (1998) Applied Hydrology, McGraw Hill pp. 201-242
- Cleveland, T.G. He, X., Asquith, W.H., Fang, X., and D.B. Thompson. (2006) "Instantaneous Unit Hydrograph Evaluation for Rainfall-Runoff Modeling of Small Watersheds in North and South Central Texas." ASCE, Journal of Irrigation and Drainage, Vol. 132, No. 5, pp. 479-485.
- Cleveland, T.G., Thompson, D.B., Fang, X., and He, X. (2008) Synthesis of Unit Hydrographs from a Digital Elevation Model ASCE, Journal of Irrigation and Drainage Engineering, Vol. 134, No. 2, pp 212-221
- Brutsaert, W. (2023) Hydrology: An Introduction: pp. 475-509 (Chapter 12 in Physical, Kindle, and linked versions)
Write a synthesis memorandum (essay; report; ....), which is a concise document that synthesizes information from multiple sources, in this case, 8 reading assignments, to provide an overview and analysis of analytical methods discussed in those readings. The memorandum is to summarize key points, identify common themes or trends across the readings, compare and contrast different methodologies, and offer conclusions based on the collective information. This document serves to distill complex information into a coherent and informative summary, highlighting the essential aspects of the analytical methods covered in the readings. Keep in mind your summarized content is to be applied to the next problem.
Problem 2¶
Bachman Branch watershed in Dallas Texas; Contour map (50 meter intervals) and shaded relief maps are displayed below. The watershed nominal drainage area is about 10 square miles. The actual gage location is LAT = $32^o51’26”$ N; LON = $96^o50’13”$ W. Coordinates pictured are meters Northing and Easting.
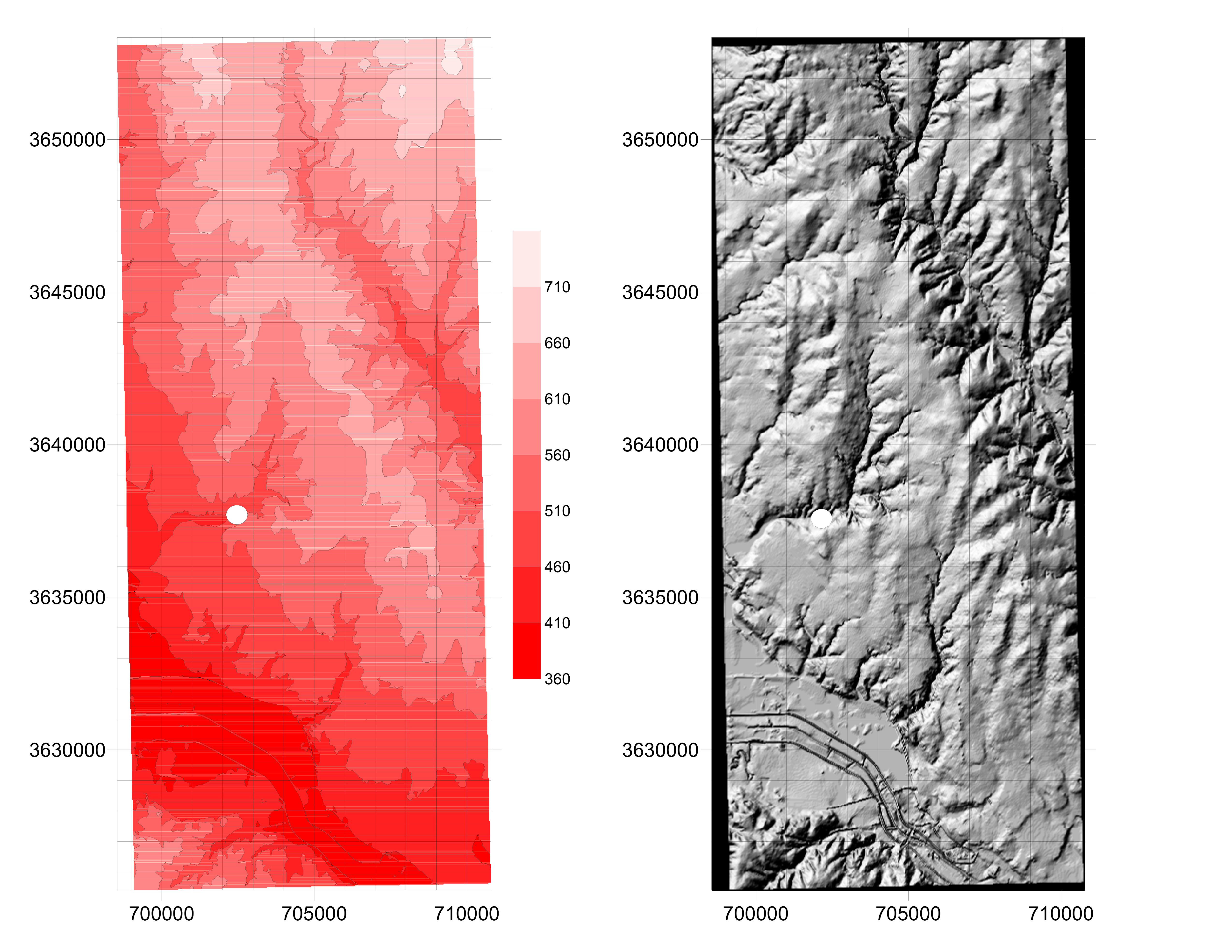
Data are from the Texas Digital Library (1st reference in list at end of this document)
Determine:
- Delineate the watershed using the map(s) above as a guide. Verify the total drainage area.
- Using Google Earth or something equivalent the CN for the entire watershed.
- Plot cumulative precipitation (in inches) versus time, and cumulative runoff (in watershed inches) versus time on the same plot. Use blue for precipitation and red for runoff.
- Using the CN; the anticipated fraction of precipitation that will become runoff.
- Using the observations; the fraction of precipitation that becomes runoff.
- Compare these results; did CN do a good job in this case?
- Convert the precipitation into incremental depths or intensities - whichever you need for the next step.
- Construct a unit hydrograph from these data, using your methods summarized from the readings above.
Precipitation
Use the last column as the distributed rainfall over the entire watershed. The "HOURS_PASSED" column is time since beginning of the rainfall event.
Data file : rain_sta08055700_1966_0617.dat
Contents:
# HYETOGRAPH FILE
# Filename=rain_sta08055700_1966_0617.dat
# site=08055700 Bachman Branch at Dallas, Texas
# latitude=32()51'36" Location 2
# longitude=96()50'12" Location 2
# drainage_area(mi2)=10.0
# DATE_TIME=date and time in MM/DD/YYYY@HH:MM
# PRECIP1=Gage 8-W raw recorded precipitation in inches
# PRECIP2=Gage 9-W raw recorded precipitation in inches
# PRECIP3=Gage 1-T raw recorded precipitation in inches
# PRECIP4=Gage 3-T raw recorded precipitation in inches
# PRECIP5=Gage 1-B raw recorded precipitation in inches
# PRECIP6=Gage 2-B raw recorded precipitation in inches
# ACCUM_WTD_PRECIP=weighted cumulative precipitation in inches
DATE_TIME HOURS_PASSED PRECIP1 PRECIP2 PRECIP3 PRECIP4 PRECIP5 PRECIP6 ACCUM_WTD_PRECIP
06/17/1966@05:15:00 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
06/17/1966@05:20:00 0.0833 0.0100 0.0100 0.0000 0.0000 0.0000 0.0100 0.0000
06/17/1966@05:25:00 0.1667 0.0100 0.0100 0.0000 0.0000 0.0000 0.0300 0.0100
06/17/1966@05:30:00 0.2500 0.0100 0.0200 0.0000 0.0500 0.0000 0.0800 0.0300
06/17/1966@05:35:00 0.3333 0.0200 0.0200 0.0000 0.1700 0.0100 0.2500 0.1100
06/17/1966@05:40:00 0.4167 0.1000 0.0400 0.0200 0.2700 0.0700 0.3300 0.1700
06/17/1966@05:45:00 0.5000 0.1400 0.1000 0.0900 0.3100 0.2100 0.3900 0.2700
06/17/1966@05:50:00 0.5833 0.2200 0.2000 0.2100 0.3500 0.4600 0.4800 0.4300
06/17/1966@06:00:00 0.7500 0.3100 0.5700 0.3200 0.5000 0.6900 0.6800 0.6200
06/17/1966@06:10:00 0.9167 0.4200 0.8400 0.5200 0.7700 0.8200 0.9600 0.8300
06/17/1966@06:20:00 1.0833 0.5600 1.0900 0.7000 1.0000 0.9900 1.1300 1.0100
06/17/1966@06:30:00 1.2500 0.6500 1.1800 0.8500 1.0300 1.1900 1.1700 1.1400
06/17/1966@06:45:00 1.5000 0.7200 1.3200 0.9400 1.0400 1.2700 1.2000 1.1800
06/17/1966@07:00:00 1.7500 0.7700 1.3600 0.9800 1.0600 1.3100 1.2400 1.2200
06/17/1966@07:15:00 2.0000 0.8200 1.4000 1.0200 1.1100 1.3300 1.2800 1.2400
06/17/1966@07:30:00 2.2500 0.8800 1.4500 1.0800 1.1300 1.3700 1.3300 1.3000
06/17/1966@07:45:00 2.5000 0.9400 1.5000 1.1100 1.1600 1.4000 1.3800 1.3500
06/17/1966@08:00:00 2.7500 1.0200 1.5600 1.1400 1.2300 1.4300 1.4200 1.3900
06/17/1966@08:15:00 3.0000 1.0600 1.6200 1.1700 1.2700 1.4900 1.4500 1.4200
06/17/1966@08:30:00 3.2500 1.1000 1.6600 1.1900 1.2900 1.5100 1.4800 1.4500
06/17/1966@08:45:00 3.5000 1.1200 1.6700 1.2200 1.3100 1.5300 1.5000 1.4700
06/17/1966@09:00:00 3.7500 1.1300 1.6900 1.2300 1.3300 1.5400 1.5100 1.4800
06/17/1966@10:00:00 4.7500 1.1400 1.7100 1.2500 1.3300 1.5400 1.5300 1.5000
06/17/1966@12:10:00 6.9167 1.1400 1.7100 1.3200 1.3400 1.5400 1.5300 1.5000
06/17/1966@12:15:00 7.0000 1.1400 1.7100 1.3300 1.3500 1.6100 1.6300 1.5600
06/17/1966@12:20:00 7.0833 1.1400 2.0000 1.3700 1.3900 1.7400 1.7100 1.6700
06/17/1966@12:25:00 7.1667 1.2600 2.1000 1.4200 1.4600 1.8700 1.7800 1.7500
06/17/1966@12:30:00 7.2500 1.2700 2.1700 1.4800 1.5000 1.9900 1.8400 1.8300
06/17/1966@12:45:00 7.5000 1.3600 2.3000 1.4900 1.5100 2.0000 1.8500 1.8500
06/17/1966@14:30:00 9.2500 1.4000 2.3000 1.5000 1.5200 2.0000 1.8500 1.8500Runoff
Use the last column as the distributed rainfall over the entire watershed. The "HOURS_PASSED" column is time since beginning of the rainfall event.
Data file: unit_sta08055700_1966_0617.dat
Contents:
# HYDROGRAPH FILE
# Filename=unit_sta08055700_1966_0617.dat
# site=08055700 Bachman Branch at Dallas, Texas
# latitude=32()51'37"
# longitude=96()50'13"
# drainage_area(mi2)=10.0
# DATE_TIME=date and time in MM/DD/YYYY@HH:MM
# RUNOFF=runoff in cubic feet per second
# ACCUM_RUNOFF=accumulated runoff in inches
DATE_TIME HOURS_PASSED RUNOFF ACCUM_RUNOFF
06/17/1966@00:00:00 0.0000 4.0000 0.0015
06/17/1966@05:00:00 5.0000 3.4000 0.0030
06/17/1966@05:31:00 5.5167 3.3000 0.0032
06/17/1966@06:00:00 6.0000 6.3000 0.0037
06/17/1966@06:31:00 6.5167 56.0000 0.0080
06/17/1966@07:00:00 7.0000 680.0000 0.0466
06/17/1966@07:15:00 7.2500 955.0000 0.0848
06/17/1966@07:31:00 7.5167 1100.0000 0.1274
06/17/1966@07:45:00 7.7500 990.0000 0.1644
06/17/1966@08:00:00 8.0000 740.0000 0.2083
06/17/1966@08:31:00 8.5167 475.0000 0.2451
06/17/1966@09:00:00 9.0000 360.0000 0.2864
06/17/1966@10:00:00 10.0000 260.0000 0.3267
06/17/1966@11:00:00 11.0000 144.0000 0.3490
06/17/1966@12:00:00 12.0000 67.0000 0.3593
06/17/1966@13:00:00 13.0000 48.0000 0.3650
06/17/1966@13:31:00 13.5167 104.0000 0.3710
06/17/1966@13:45:00 13.7500 380.0000 0.3852
06/17/1966@14:00:00 14.0000 600.0000 0.4084
06/17/1966@14:15:00 14.2500 475.0000 0.4274
06/17/1966@14:31:00 14.5167 380.0000 0.4495
06/17/1966@15:00:00 15.0000 260.0000 0.4794
06/17/1966@16:00:00 16.0000 104.0000 0.4955
06/17/1966@17:00:00 17.0000 48.0000 0.5029
06/17/1966@18:00:00 18.0000 31.0000 0.5101
06/17/1966@20:00:00 20.0000 17.0000 0.5153
06/17/1966@22:00:00 22.0000 13.0000 0.5194
06/18/1966@00:00:00 24.0000 9.8000 0.5209Need tools to read files:
# file reader functions
# read precipitation file
def readPrecip(filename,colAccP):
precipitation = []
externalfile = open(filename,'r') # create connection to file, set to read (r), file must exist
for line in externalfile:
if line[0] == '#' or line[0] == "D" : # skip comments and header row
continue
else:
precipitation.append([str(n) for n in line.strip().split()])
externalfile.close()
plen = len(precipitation)
# parse the file
timeP = [0.0 for i in range(plen)]
depthP = [0.0 for i in range(plen)]
for i in range(plen):
timeP[i]=float(precipitation[i][1])
depthP[i]=float(precipitation[i][colAccP])
#for i in range(plen):
# print(timeP[i],depthP[i])
return (timeP,depthP)
# read runoff file
def readRunoff(filename,colAccQ):
discharge = []
externalfile = open(filename,'r') # create connection to file, set to read (r), file must exist
for line in externalfile:
if line[0] == '#' or line[0] == "D" : # skip comments and header row
continue
else:
discharge.append([str(n) for n in line.strip().split()])
externalfile.close()
qlen = len(discharge)
# parse the file
timeQ = [0.0 for i in range(qlen)]
depthQ = [0.0 for i in range(qlen)]
for i in range(qlen):
timeQ[i]=float(discharge[i][1])
depthQ[i]=float(discharge[i][colAccQ])
#for i in range(qlen):
# print(timeQ[i],depthQ[i])
return(timeQ,depthQ)
Need tools to make plots
# plotting functions
import matplotlib.pyplot as plt
def Plot2Lines(list1,list2,list3,list4,ptitle,xlabel,ylabel,legend1,legend2):
# Create a line chart of list2,list4 on y axis and list1,list3 on x axis
mydata = plt.figure(figsize = (18,6)) # build a drawing canvass from figure class; aspect ratio 4x3
plt.plot(list1, list2, c='red', marker='.',linewidth=2) # basic line plot
plt.plot(list3, list4, c='blue', marker='.',linewidth=1) # basic line plot
plt.xlabel(xlabel) # label the x-axis
plt.ylabel(ylabel) # label the y-axis, notice the LaTex markup
plt.legend([legend1,legend2]) # legend for each series
plt.title(ptitle) # make a plot title
# plt.xlim(100000, 120000)
# plt.ylim(2700, 2850)
plt.grid() # display a grid
plt.show() # display the plot
return()
def Plot2Stairs(list1,list2,list3,list4,ptitle,xlabel,ylabel,legend1,legend2):
# Create a line chart of list2,list4 on y axis and list1,list3 on x axis
mydata = plt.figure(figsize = (18,6)) # build a drawing canvass from figure class; aspect ratio 4x3
plt.step(list1, list2, c='red', marker='.',linewidth=2) # basic line plot
plt.step(list3, list4, c='blue', marker='.',linewidth=1) # basic line plot
plt.xlabel(xlabel) # label the x-axis
plt.ylabel(ylabel) # label the y-axis, notice the LaTex markup
plt.legend([legend1,legend2]) # legend for each series
plt.title(ptitle) # make a plot title
# plt.xlim(100000, 120000)
# plt.ylim(2700, 2850)
plt.grid() # display a grid
plt.show() # display the plot
return()
- Read the two files and prepare four lists
precipdata = readPrecip("rain_sta08055700_1966_0617.dat",8)
runoffdata = readRunoff("unit_sta08055700_1966_0617.dat",3)
# split into lists
timeP = precipdata[0]
depthP = precipdata[1]
timeQ = runoffdata[0]
depthQ = runoffdata[1]
- Plot cumulative precipitation (in inches) versus time, and cumulative runoff (in watershed inches) versus time on the same plot. Use blue for precipitation and red for runoff.
# plot the data
xlabel = 'Time (hours)'
ylabel = 'Depth (inches)'
legend1 = 'Cumulative Runoff in watershed inches'
legend2 = 'Cumulative Precipitation in inches'
ptitle = 'Plot of Rainfall-Runoff for STA08055700 Storm June 17, 1966'
Plot2Lines(timeQ,depthQ,timeP,depthP,ptitle,xlabel,ylabel,legend1,legend2);
- Now append one or both terms of series so are same length
# make the two time series same length
bigtime = max(timeP[-1],timeQ[-1])
# add a row all series to get same time base
timeP.append(float(bigtime+1)) # just add 1 row to the series
timeQ.append(float(bigtime+1))
depthP.append(depthP[-1]) # extend the last element
depthQ.append(depthQ[-1])
print(timeQ)
# now plot again!
Plot2Lines(timeQ,depthQ,timeP,depthP,ptitle,xlabel,ylabel,legend1,legend2);
- Usually desirable to have time increments same length (i.e. every hour, every minute, ...). Use interpolation to map above data onto 1 hour intervals. Will need an interpolation tool - a simple to use tool is:
import numpy as np
from scipy.interpolate import interp1d
def interpolate_xy_pairs(x_values, y_values, new_x_values):
"""
Interpolate a set of X-Y pairs onto a new list of uniformly spaced X values.
Parameters:
x_values (list): List of original X values.
y_values (list): List of original Y values.
new_x_values (list): List of uniformly spaced new X values for interpolation.
Returns:
list: List of interpolated Y values corresponding to new_x_values.
"""
# Perform linear interpolation
interp_func = interp1d(x_values, y_values, kind='linear')
# Interpolate onto new X values
interpolated_y_values = interp_func(new_x_values)
return interpolated_y_values
- Set up the desired time list (hours 0 - 25 in this exercise), then interpolate and plot - change to the stair plot (it improves clarity)
t_model = [i for i in range(int(timeP[-1]+1))]
# Interpolate
q_model = interpolate_xy_pairs(timeQ, depthQ, t_model)
p_model = interpolate_xy_pairs(timeP, depthP, t_model)
ptitle = ptitle + '\n Interpolated onto 1-hour intervals'
Plot2Stairs(t_model,q_model,t_model,p_model,ptitle,xlabel,ylabel,legend1,legend2);
- It is useful to be able to convert into incremental rates; backward differencing is appropraite for these data (assuming the roll-on and roll-off part of the lists have zero slope.)
# cumulative/incremental functions (old R code)
# get slope from two points in XY space
def slope(f1,f2,x1,x2):
slope = (f2-f1)/(x2-x1)
return slope
# cumulative to incremental
def disaggregate(x,y):
'''
x and y are equal length lists
returns a new list containing the incremental changes along x-axis
'''
if len(x) != len(y):
raise ValueError("lists are different length in disaggregate")
n=len(x) # length of vectors
dfdx=[0 for i in range(n)]; # dfdx starts as list of zeros
for i in range(1,n):
dfdx[i] = (y[i] - y[i-1])/(x[i]- x[i-1])
return dfdx
# incremental to cumulative
def aggregate(vector1,vector2):
n=len(vector1)
# fill vector2 with zeros
vector2 = [0 for i in range(n)]
vector2[0] = vector1[0]+0.0
for i in range(1,n):
vector2[i] = vector2[i-1] + vector1[i]
return vector2
# compute incremental values
incremental_rain = disaggregate(t_model,p_model)
incremental_flow = disaggregate(t_model,q_model)
# plot the data
xlabel = 'Time (hours)'
ylabel = 'Rate (inches/hour)'
legend1 = 'Runoff'
legend2 = 'Precipitation'
ptitle = 'Plot of Rainfall-Runoff for STA08055700 Storm June 17, 1966'
Plot2Stairs(t_model,incremental_flow,t_model,incremental_rain,ptitle,xlabel,ylabel,legend1,legend2);
- Now have the incremental inputs and outputs At this point we can worry about loss model.
- Here we build a CN model here is a script using method described at Creating_excess_precipitation
#CN loss model on cumulative lists
def xsrain(cumP,CN):
S = (1000/CN)-10.0
Ia = 0.2*S
if cumP >= Ia:
xsrain=S*(cumP-Ia)/(cumP-Ia+S)
else:
xsrain=0.0
return xsrain
# Apply CN model
CN = 93
excess_p = [0 for i in range(len(p_model))]
for i in range(len(p_model)):
excess_p[i] = xsrain(p_model[i],CN) # p_model should be in cumulative space
# Convert into rates for unitgraph analysis
excess_r = []
excess_r = disaggregate(t_model,excess_p)
#excess_rain
# plot the data
xlabel = 'Time (hours)'
ylabel = 'Rate (inches/hour)'
legend1 = 'Raw Rain'
legend2 = 'Excess Rain'
ptitle = 'Plot of Excess Rain for STA08055700 Storm June 17, 1966 \n CN = '+repr(CN)
Plot2Stairs(t_model,incremental_rain,t_model,excess_r,ptitle,xlabel,ylabel,legend1,legend2);
- Now check total volumes; by unitgraph requirements; $\int P_{xs} = \int Q_{obs}$
print("Total Runoff : ",sum(incremental_flow))
print("Total Excess : ",sum(excess_r))
That's probably close enough of a volume balance
- Now that have excess and runoff in same units and same time scale
- Now construct a kernel function: $u(t)=\frac{K}{\Gamma(N)}(\frac{2}{\bar t})(\frac{t}{\bar t})^{2N-1}e^{(\frac{t}{\bar t})^\beta}$
def kernelfn(tbar,time,scale=2,shape=3,beta=2):
'''
kernel function for a unit hydrograph - uses a gamma-type hydrograph
scale: a scaling parameter, should be 2, but left adjustable for grins
shape: Nash's reservoir number
tbar: Characteristic time, lag time in NRCS, time-to-peak,
and time-of-concentration are all similar concepts.
beta: Exponent controling decay rate in exponential part of function;
Should be a 2 or 3 for typical watersheds, but left adjusible for
ornery cases.
'''
import math
term1 = (scale/tbar)/math.gamma(shape)
term2 = (time)/tbar
term3 = term2**(2*shape-1)
term4 = math.exp(-1*term2**beta)
kernelfn = term1*term3*term4
return kernelfn
# discrete convolution function
def convolve(duration, excitation, kernel):
response = [0 for i in range(duration)] # populate response vector with zeros
# response = direct runoff hydrograph (unscaled)
# excitation = input rate in length per time
# kernel = unit response
for i in range(duration):
for j in range(i,duration-1):
response[j]=excitation[i]*kernel[(j-i)+1]+response[j]
return(response)
#def convolve(N1,excitation,kernel):
# N1 is length of kernel list (already populated)
# excitation is list of inputs (aka rainfall)
# kernel is list of unit responses
# response is convolved response
# response = [0.0 for i in range(N1)] # populate response vector with zeros
# for i in range(1,N1):
# for j in range(i,N1):
# response[j] = excitation[i]*kernel[(j-i)]+response[j]
# return response
# now build the runoff hydrograph
N1 = len(excess_r)
kernel = []
### parameters by trial-and-error
scale = 2 # a scale constant - has units of rate
shape = 7 # a shape parameter
tbar = 3.5 # timing parameter - has units of time
beta = 2 # dispersion parameter
# the actual UH kernel
for i in range(N1):
kernel.append(kernelfn(tbar,t_model[i],scale,shape,beta))
# the convolution
response = convolve(N1,excess_r,kernel)
# plotting results
legend1 = 'Observed Hydrograph'
legend2 = 'Model Hydrograph'
ptitle = "Fitted Hydrograph" + \
"\n Volume Error Ratio (observed/model) " \
+ repr(round(sum(incremental_flow)/sum(response),3))\
+ "\n Peak Error Ratio (observed/model) " \
+ repr(round(max(incremental_flow)/max(response),3)) \
+ "\n Kernel Integral : " + repr(round(sum(kernel)))
Plot2Stairs(t_model,incremental_flow,t_model,response,ptitle,xlabel,ylabel,legend1,legend2);
#ptitle="Kernel Function"
#Plot2Stairs(t_model,kernel,t_model,kernel,ptitle,xlabel,ylabel,legend1,legend2);
A quick check is to plot as rainfall-runoff
# plotting results
legend1 = 'Observed Hydrograph'
legend2 = 'Input Hyetograph'
Plot2Stairs(t_model,q_model,t_model,p_model,ptitle,xlabel,ylabel,legend1,legend2);
# plotting results
legend1 = 'Model Hydrograph'
legend2 = 'Input Hyetograph'
accResponse = [0 for i in range(len(response))]
accResponse = aggregate(response,accResponse)
Plot2Stairs(t_model,accResponse,t_model,p_model,ptitle,xlabel,ylabel,legend1,legend2);
# plotting results
legend1 = 'Observed Hydrograph'
legend2 = 'Model Hydrograph'
accResponse = [0 for i in range(len(response))]
accResponse = aggregate(response,accResponse)
Plot2Lines(t_model,q_model,t_model,accResponse,ptitle,xlabel,ylabel,legend1,legend2);
Scale is about right - so our model is completed we would report results as:
$u(t)=\frac{2}{\Gamma(7)}(\frac{2}{4})(\frac{t}{4})^{13}e^{-(\frac{t}{4})^2}$
or simply the parameters as:
$\bar t ~ \approx 3\frac{1}{2}~\text{hours}$
$N ~\approx 7$
As a tangential examination, lets perform the entire analysis at finer (1 minute) time resolutions
########################
# read the input files #
########################
precipdata = readPrecip("rain_sta08055700_1966_0617.dat",8)
runoffdata = readRunoff("unit_sta08055700_1966_0617.dat",3)
# split into lists
timeP = precipdata[0]
depthP = precipdata[1]
timeQ = runoffdata[0]
depthQ = runoffdata[1]
########################################
# make the two time series same length #
########################################
bigtime = max(timeP[-1],timeQ[-1])
# add a row all series to get same time base
timeP.append(float(bigtime+1)) # just add 1 row to the series
timeQ.append(float(bigtime+1))
depthP.append(depthP[-1]) # extend the last element
depthQ.append(depthQ[-1])
#print(timeQ)
############
# now plot #
############
legend1 = 'Observed Hydrograph'
legend2 = 'Observed Rainfall'
Plot2Lines(timeQ,depthQ,timeP,depthP,ptitle,xlabel,ylabel,legend1,legend2);
########################################
# Interpolate onto 1-minute time steps #
########################################
bigtime = 60.0*timeQ[-1] # convert hours to minutes
t_model = [float(i) for i in range(int(bigtime)+1)]
minQ = [0 for i in range(len(timeQ))]
for i in range(len(minQ)):
minQ[i]=60.0*timeQ[i] # convert data from hours to minutes
minP = [0 for i in range(len(timeP))]
for i in range(len(minP)):
minP[i]=60.0*timeP[i] # convert data from hours to minutes
q_model = interpolate_xy_pairs(minQ, depthQ, t_model)
p_model = interpolate_xy_pairs(minP, depthP, t_model)
xlabel = 'Time (minutes)'
ylabel = 'Cumulative Depth (inches)'
legend1 = 'Runoff - 1 minute increments'
legend2 = 'Precipitation - 1 minute increments'
ptitle = 'Plot of Rainfall-Runoff for STA08055700 Storm June 17, 1966 \n Data interpolated onto 1-hour increments'
Plot2Lines(t_model,q_model,t_model,p_model,ptitle,xlabel,ylabel,legend1,legend2);
##############################
# Compute incremental values #
##############################
incremental_rain = disaggregate(t_model,p_model)
incremental_flow = disaggregate(t_model,q_model)
# plot the data
xlabel = 'Time (minutes)'
ylabel = 'Rate (inches/minute)'
legend1 = 'Runoff (inches/minute)'
legend2 = 'Precipitation (inches/minute)'
ptitle = 'Plot of Rainfall-Runoff for STA08055700 Storm June 17, 1966'
Plot2Stairs(t_model,incremental_flow,t_model,incremental_rain,ptitle,xlabel,ylabel,legend1,legend2);
##################
# Apply CN model #
##################
CN = 93
excess_p = [0 for i in range(len(p_model))]
for i in range(len(p_model)):
excess_p[i] = xsrain(p_model[i],CN) # p_model should be in cumulative space
# Convert into rates for unitgraph analysis
excess_r = []
excess_r = disaggregate(t_model,excess_p)
#excess_rain
# plot the data
xlabel = 'Time (minutes)'
ylabel = 'Rate (inches/minute)'
legend1 = 'Raw Rain'
legend2 = 'Excess Rain'
ptitle = 'Plot of Excess Rain for STA08055700 Storm June 17, 1966 \n CN = '+repr(CN)
Plot2Stairs(t_model,incremental_rain,t_model,excess_r,ptitle,xlabel,ylabel,legend1,legend2);
##########################################
# Check total volumes - should be close! #
##########################################
print("Total Runoff : ",sum(incremental_flow))
print("Total Excess : ",sum(excess_r))
# now build the runoff hydrograph
N1 = len(excess_r)
kernel = []
### parameters by trial-and-error
scale = 2 # a scale constant - has units of rate
shape = 7 # a shape parameter
tbar = 180 # timing parameter - has units of time (changed onto minutes)
beta = 2 # dispersion parameter
# the actual UH kernel
for i in range(N1):
kernel.append(kernelfn(tbar,t_model[i],scale,shape,beta))
# the convolution
response = convolve(N1,excess_r,kernel)
# plotting results
legend1 = 'Observed Hydrograph'
legend2 = 'Model Hydrograph'
ptitle = "Fitted Hydrograph" + \
"\n Volume Error Ratio (observed/model) " \
+ repr(round(sum(incremental_flow)/sum(response),3))\
+ "\n Peak Error Ratio (observed/model) " \
+ repr(round(max(incremental_flow)/max(response),3)) \
+ "\n Kernel Integral : " + repr(round(sum(kernel)))
Plot2Stairs(t_model,incremental_flow,t_model,response,ptitle,xlabel,ylabel,legend1,legend2);
#ptitle="Kernel Function"
#Plot2Stairs(t_model,kernel,t_model,kernel,ptitle,xlabel,ylabel,legend1,legend2);
# plotting results
legend1 = 'Observed Hydrograph'
legend2 = 'Input Hyetograph'
Plot2Stairs(t_model,q_model,t_model,p_model,ptitle,xlabel,ylabel,legend1,legend2);
# plotting results
legend1 = 'Model Hydrograph'
legend2 = 'Input Hyetograph'
accResponse = [0 for i in range(len(response))]
accResponse = aggregate(response,accResponse)
Plot2Stairs(t_model,accResponse,t_model,p_model,ptitle,xlabel,ylabel,legend1,legend2);
# plotting results
legend1 = 'Observed Hydrograph'
legend2 = 'Model Hydrograph'
accResponse = [0 for i in range(len(response))]
accResponse = aggregate(response,accResponse)
Plot2Stairs(t_model,q_model,t_model,accResponse,ptitle,xlabel,ylabel,legend1,legend2);
Now the parameters are:
$\bar t ~ \approx 210~\text{minutes}$
$N ~\approx 7$
The timing of the peak is important, so that is what is usually optimized, followed by the volume (to ensure mass balance), finally magnitude of the peak.
This is about as good as we can get with this particular unit hydrograph kernel; we could construct other kernels, and maybe get the second peak - in this case its a consequence of the loss model.
Problem 3¶
Apply the unit hydrograph, and your preferred loss model (CN, Green-Ampt, Observation Ratio, ...) to the following storm, and make a plot similar to the observation plots above.
Data file: rain_sta08055700_1976_0618.dat
Contents:
# HYETOGRAPH FILE
# Filename=rain_sta08055700_1976_0618.dat
# site=08055700 Bachman Branch at Dallas, Texas
# latitude=32()51'37" Location 5
# longitude=96()50'13" Location 5
# drainage_area(mi2)=10.0
# DATE_TIME=date and time in MM/DD/YYYY@HH:MM
# PRECIP1=Gage 1-B raw recorded precipitation in inches
# recorded as cum. Weighted calculated by UH team
DATE_TIME HOURS_PASSED PRECIP1 ACCUM_WTD_PRECIP
06/18/1976@06:00:00 0.0000 0.0000 0.0000
06/18/1976@08:00:00 2.0000 0.0300 0.0300
06/18/1976@08:15:00 2.2500 0.3000 0.3000
06/18/1976@08:30:00 2.5000 1.2000 1.2000
06/18/1976@08:45:00 2.7500 1.4100 1.4100
06/18/1976@09:00:00 3.0000 1.5900 1.5900
06/18/1976@09:15:00 3.2500 1.6500 1.6500
06/18/1976@09:30:00 3.5000 1.6700 1.6700
06/18/1976@09:45:00 3.7500 1.7000 1.7000
06/18/1976@10:00:00 4.0000 1.7000 1.7000
06/18/1976@10:30:00 4.5000 1.7100 1.7100
06/18/1976@11:00:00 5.0000 1.7100 1.7100
06/18/1976@11:30:00 5.5000 1.8000 1.8000The observed hydrograph will be supplied after the due date, closest to the observed hydrograph will get a prize.
########################
# read the input files #
########################
precipdata = readPrecip("rain_sta08055700_1976_0618.dat",3)
# split into lists
timeP = precipdata[0]
depthP = precipdata[1]
##############################
# extend series to 24 hours #
##############################
timeP.append(24.0)
depthP.append(depthP[-1])
########################################
# Interpolate onto 1-minute time steps #
########################################
bigtime = 1440 # 24 hours in minutes
t_model = [float(i) for i in range(int(bigtime)+1)]
#print(t_model)
minP = [0 for i in range(len(timeP))]
for i in range(len(minP)):
minP[i]=60.0*timeP[i] # convert data from hours to minutes
p_model = interpolate_xy_pairs(minP, depthP, t_model)
##############################
# Compute incremental values #
##############################
incremental_rain = disaggregate(t_model,p_model)
##################
# Apply CN model #
##################
CN = 93
excess_p = [0 for i in range(len(p_model))]
for i in range(len(p_model)):
excess_p[i] = xsrain(p_model[i],CN) # p_model should be in cumulative space
# Convert into rates for unitgraph analysis
excess_r = []
excess_r = disaggregate(t_model,excess_p)
#excess_rain
###############################
# Build the runoff hydrograph #
###############################
N1 = len(excess_r)
kernel = []
### parameters by trial-and-error
scale = 2 # a scale constant - has units of rate
shape = 7 # a shape parameter
tbar = 180 # timing parameter - has units of time (changed onto minutes)
beta = 2 # dispersion parameter
# the actual UH kernel
for i in range(N1):
kernel.append(kernelfn(tbar,t_model[i],scale,shape,beta))
# the convolution
response = convolve(N1,excess_r,kernel)
# plotting results
legend1 = 'Observed Precipitation'
legend2 = 'Predicted Hydrograph'
ptitle = "Predicted Hydrograph for sta08055700_1976_0618"
Plot2Stairs(t_model,excess_r,t_model,response,ptitle,xlabel,ylabel,legend1,legend2);
Naturally I already have the solution data, here is the plot of the prediction and actual hydrographs.
runoffdata = readRunoff("unit_sta08055700_1976_0618.dat",3)
timeQ = runoffdata[0]
depthQ = runoffdata[1]
##############################
# extend series to 24 hours #
##############################
timeQ.append(24.0)
depthQ.append(depthQ[-1])
minQ = [0 for i in range(len(timeQ))]
for i in range(len(minQ)):
minQ[i]=60.0*timeQ[i] # convert data from hours to minutes
q_model = interpolate_xy_pairs(minQ, depthQ, t_model)
# plotting results
legend1 = 'Observed Hydrograph'
legend2 = 'Model Hydrograph'
accResponse = [0 for i in range(len(response))]
accResponse = aggregate(response,accResponse)
Plot2Stairs(t_model,q_model,t_model,accResponse,ptitle,xlabel,ylabel,legend1,legend2);