¶

Decision trees, AKA Classification And Regression Tree (CART) models, are extremely intuitive ways to classify or label objects: you simply ask a series of questions designed to zero-in on the classification. For example, if you wanted to build a decision tree to classify an animal you come across while on a hike, you might construct the one shown here:
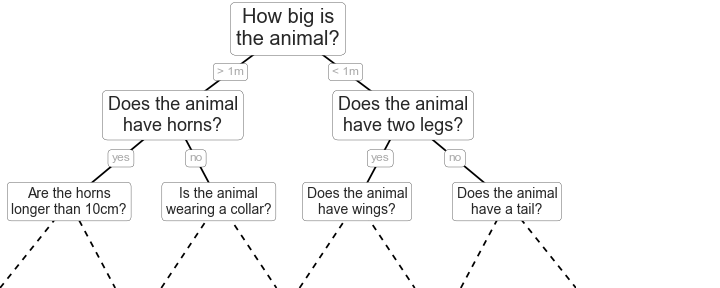
The binary splitting makes this extremely efficient: in a well-constructed tree, each question will cut the number of options by approximately half, very quickly narrowing the options even among a large number of classes. The trick, of course, comes in deciding which questions to ask at each step. In machine learning implementations of decision trees, the questions generally take the form of axis-aligned splits in the data: that is, each node in the tree splits the data into two groups using a cutoff value within one of the features. Let’s now look at an example of this.
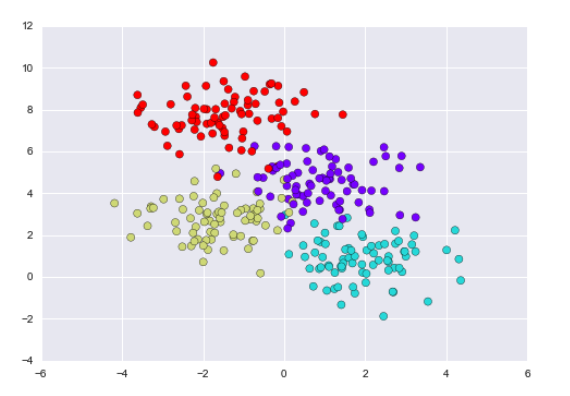
A simple decision tree built on this data will iteratively split the data along one or the other axis according to some quantitative criterion, and at each level assign the label of the new region according to a majority vote of points within it. This figure presents a visualization of the first four levels of a decision tree classifier for this data:

Note
After the first split, every point in the upper branch remains unchanged, so there is no need to further subdivide this branch. Except for nodes that contain all of one color, at each level every region is again split along one of the two features.
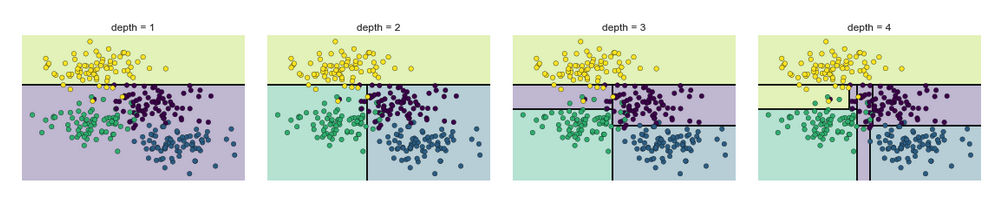
Notice that as the depth increases, we tend to get very strangely shaped classification regions; for example, at a depth of five, there is a tall and skinny purple region between the yellow and blue regions. It’s clear that this is less a result of the true, intrinsic data distribution, and more a result of the particular sampling or noise properties of the data. That is, this decision tree, even at only five levels deep, is clearly over-fitting our data, as evident in the pecular shapes of the classification regions below.
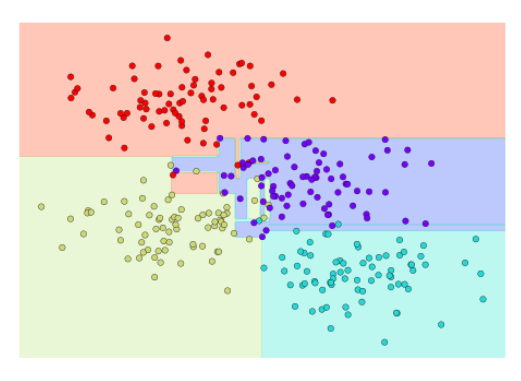
Such over-fitting turns out to be a general drawback of decision trees: it is very easy to go too deep in the tree, and thus to fit details of the particular data rather than the overall properties of the distributions they are drawn from. Another way to see this over-fitting is to look at models trained on different subsets of the data—for example, in this figure we train two different trees, each on half of the original data:
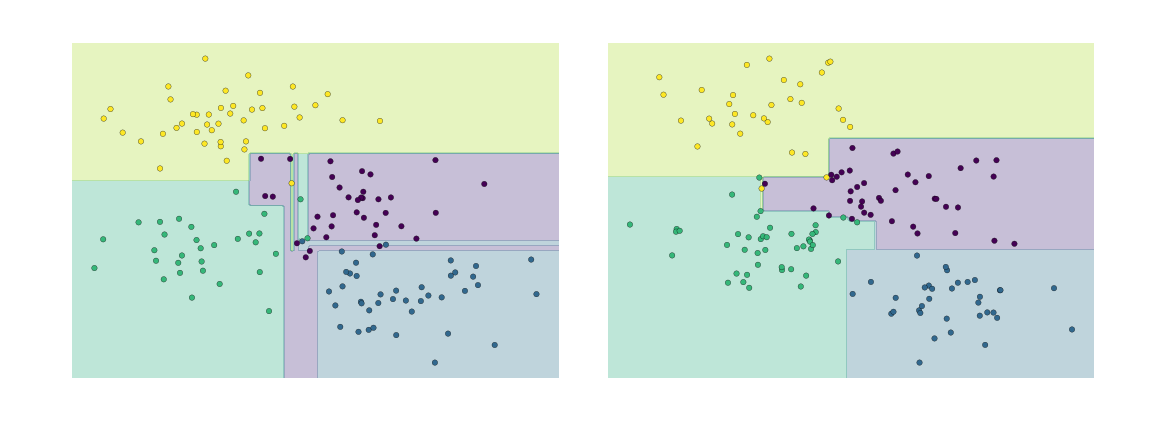
It is clear that in some places, the two trees produce consistent results (e.g., in the four corners), while in other places, the two trees give very different classifications (e.g., in the regions between any two clusters). The key observation is that the inconsistencies tend to happen where the classification is less certain, and thus by using information from both of these trees, we might come up with a better result!
Note
In signal processing a similar concept called solution stacking is employed to improve instrument resolution “after the fact.” Synthetic Arpature Radar (SAR) is a good example of solution stacking (a kind of regression tree) to improve apparent signal resolution>
Just as using information from two trees improves our results, we might expect that using information from many trees would improve our results even further. AND WHAT WOULD WE HAVE IF WE HAD MANY TREES?
YES! A FOREST! (If we had many Ents (smart trees ;) ), we could have Fangorn Forest!)

This notion—that multiple overfitting estimators can be combined to reduce the effect of this overfitting—is what underlies an ensemble method called bagging. Bagging makes use of an ensemble (a grab bag, perhaps) of parallel estimators, each of which over-fits the data, and averages the results to find a better classification. An ensemble of randomized decision trees is known as a random forest.
What is Random Forest?¶
Random Forest is a versatile machine learning method capable of performing both regression and classification tasks. It also undertakes dimensional reduction methods, treats missing values, outlier values and other essential steps of data exploration, and does a fairly good job. It is a type of ensemble learning method, where a group of weak models combine to form a powerful model.
In Random Forest, we grow multiple trees. To classify a new object based on attributes, each tree gives a classification and we say the tree “votes” for that class. The forest chooses the classification having the most votes (over all the trees in the forest) and in case of regression, it takes the average of outputs by different trees.

How Random Forest algorithm works?¶
Random forest is like bootstrapping algorithm with Decision tree (CART) model. Say, we have 1000 observation in the complete population with 10 variables. Random forest tries to build multiple CART models with different samples and different initial variables. For instance, it will take a random sample of 100 observation and 5 randomly chosen initial variables to build a CART model. It will repeat the process (say) 10 times and then make a final prediction on each observation. Final prediction is a function of each prediction. This final prediction can simply be the mean of each prediction. Let’s consider an imaginary example:
Out of a large population, Say, the algorithm Random forest picks up 10k observation with only one variable (for simplicity) to build each CART model. In total, we are looking at 5 CART model being built with different variables. In a real life problem, you will have more number of population sample and different combinations of input variables. The target variable is the salary bands:
Band1 : Below 40000
Band2 : 40000 - 150000
Band3 : Above 150000
Following are the outputs of the 5 different CART model:
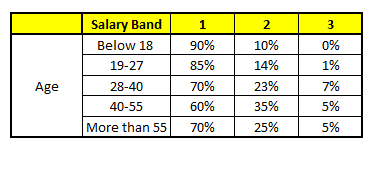
CART1 : Based on “Age” as predictor:¶
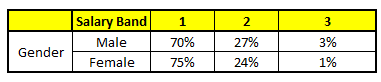
CART2 : Based on “Gender” as predictor:¶
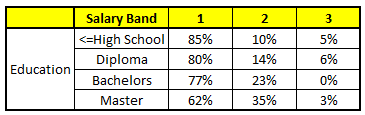
CART3 : Based on “Education” as predictor:¶
CART4 : Based on “Residence” as predictor:¶

CART5 : Based on “Industry” as predictor:¶
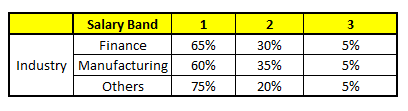
Using these 5 CART models, we need to come up with single set of probability to belong to each of the salary classes. For simplicity, we will just take a mean of probabilities in this case study. Other than simple mean, we also consider vote method to come up with the final prediction. To come up with the final prediction let’s locate the following profile in each CART model:
Age : 35 years
Gender : Male
Highest Educational Qualification : Diploma holder
Industry : Manufacturing
Residence : Metro
For each of these CART model, following is the distribution across salary bands :
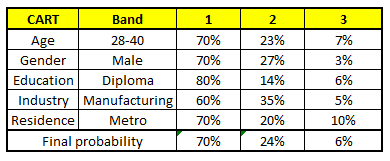
The final probability is simply the average of the probability in the same salary bands in different CART models. As you can see from this analysis, that there is 70% chance of this individual falling in class 1 (less than 40,000) and around 24% chance of the individual falling in class 2.
Example Re-using the Iris Plants Classification
¶
The Iris Flower Dataset involves predicting the flower species given measurements of iris flowers. The Iris Data Set contains information on sepal length, sepal width, petal length, petal width all in cm, and class of iris plants. The data set contains 3 classes of 50 instances each.

Let’s use Random Forest in Python and see if we can classifity iris plants based on the four given predictors.
Note
The Iris classification example that follows is largely sourced from:
Fisher,R.A. “The use of multiple measurements in taxonomic problems” Annual Eugenics, 7, Part II, 179-188 (1936); also in “Contributions to Mathematical Statistics” (John Wiley, NY, 1950).
Duda,R.O., & Hart,P.E. (1973) Pattern Classification and Scene Analysis. (Q327.D83) John Wiley & Sons. ISBN 0-471-22361-1. See page 218.
Dasarathy, B.V. (1980) “Nosing Around the Neighborhood: A New System Structure and Classification Rule for Recognition in Partially Exposed Environments”. IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. PAMI-2, No. 1, 67-71.
Gates, G.W. (1972) “The Reduced Nearest Neighbor Rule”. IEEE Transactions on Information Theory, May 1972, 431-433.
See also: 1988 MLC Proceedings, 54-64. Cheeseman et al’s AUTOCLASS II conceptual clustering system finds 3 classes in the data.
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import sklearn.metrics as metrics
import seaborn as sns
%matplotlib inline
# Read the remote directly from its url (Jupyter):
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
# Assign colum names to the dataset
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
# Read dataset to pandas dataframe
dataset = pd.read_csv(url, names=names)
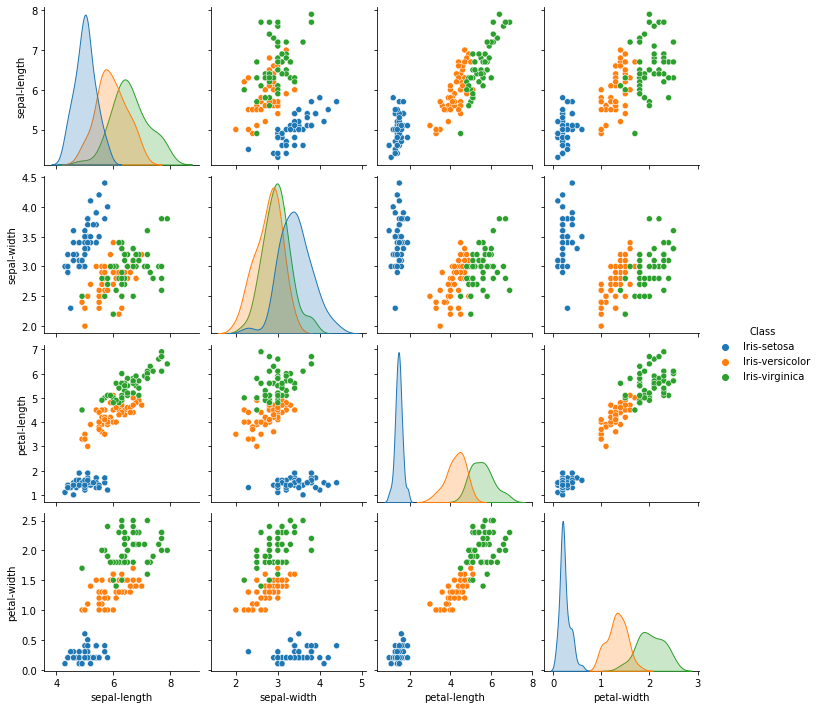
sns.pairplot(dataset, hue='Class') #A very cool plot to explore a dataset
# Notice that iris-setosa is easily identifiable by petal length and petal width,
# while the other two species are much more difficult to distinguish.
<seaborn.axisgrid.PairGrid at 0xffff86c24d60>
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.75)
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100, oob_score=True, random_state=123456)
rf.fit(X_train, y_train)
predicted = rf.predict(X_test)
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, predicted))
print(metrics.classification_report(y_test, y_pred=predicted))
[[40 0 0]
[ 0 35 3]
[ 0 2 33]]
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 40
Iris-versicolor 0.95 0.92 0.93 38
Iris-virginica 0.92 0.94 0.93 35
accuracy 0.96 113
macro avg 0.95 0.95 0.95 113
weighted avg 0.96 0.96 0.96 113
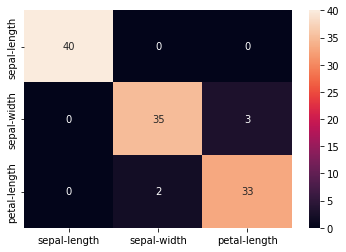
cm = pd.DataFrame(confusion_matrix(y_test, predicted), columns=names[0:3], index=names[0:3])
sns.heatmap(cm, annot=True)
#This lets us know that our model correctly separates the setosa examples,
#but exhibits a small amount of confusion when attempting to distinguish between versicolor and virginica.
<AxesSubplot:>
Engineering Application(s) Examples¶
General Observations Regarding Random Forests¶
Pros:¶
this algorithm can solve both type of problems i.e. classification and regression and does a decent estimation at both fronts.
It is effective in high dimensional spaces.
One of the most essential benefits of Random forest is, the power to handle large data sets with higher dimensionality. It can handle thousands of input variables and identify most significant variables so it is considered as one of the dimensionality reduction methods. Further, the model outputs Importance of variable, which can be a very handy feature.
It has an effective method for estimating missing data and maintains accuracy when a large proportion of the data are missing.
It has methods for balancing errors in datasets where classes are imbalanced.
The capabilities of the above can be extended to unlabeled data, leading to unsupervised clustering, data views and outlier detection.
Both training and prediction are very fast, because of the simplicity of the underlying decision trees. In addition, both tasks can be straightforwardly parallelized, because the individual trees are entirely independent entities.**
The nonparametric model is extremely flexible, and can thus perform well on tasks that are under-fit by other estimators.
Cons:¶
It surely does a good job at classification but not as good as for regression problem as it does not give continuous output. In case of regression, it doesn’t predict beyond the range in the training data, and that they may over-fit data sets that are particularly noisy.
Random Forest can feel like a black box approach for statistical modelers – you have very little control on what the model does. You can at best – try different parameters and random seeds!
References¶
Chan, Jamie. Machine Learning With Python For Beginners: A Step-By-Step Guide with Hands-On Projects (Learn Coding Fast with Hands-On Project Book 7) (p. 2). Kindle Edition.
Rashid, Tariq. Make Your Own Neural Network. . Kindle Edition.
In-Depth: Decision Trees and Random Forests” by Jake VanderPlas
Powerful Guide to learn Random Forest (with codes in R & Python)” by SUNIL RAY
Introduction to Random forest – Simplified” by TAVISH SRIVASTAVA
“Random Forest Algorithm with Python and Scikit-Learn” by Usman Malik
Videos¶
“Decision Tree (CART) - Machine Learning Fun and Easy” by Augmented Startups
2.”StatQuest: Random Forests Part 1 - Building, Using and Evaluating” by StatQuest with Josh Starmer“StatQuest: Random Forests Part 2: Missing data and clustering” by StatQuest with Josh Starmer
4.”Random Forest - Fun and Easy Machine Learning” by Augmented Startups
