Pipe Networks¶

Network Hydraulics

Examples

Note

This lesson introduces specalized software. The portions below on installation are Architecture Specific.

Pipeline Network Simulation¶

Note

The network simulator uses input files to convey the network to the program These files are listed below.

PipeNetwork.txt

4
6
200 200 200 200
00 0.67 0.67 0.67 0.67 0.5
800 700 700 800 600
00001 0.00001 0.00001 0.00001 0.00001 0.00001
000011
1 1 1 1 1
-1 0 -1 0 0
1 -1 0 0 1
0 0 1 -1 -1
0 1 0 1 0
4 3 1 -100 0 0 0 0 0 

Background: Pipelines and Networks¶

Pipe networks are analyzed for head losses in order to size pumps, determine demand management strategies, and precict minimum pressures in the system.

Pipe Networks – Topology¶

Network topology refers to the layout and connections.
Networks are built of nodes (junctions) and arcs (links).

Continunity (at a node)¶

Water is considered incompressible in steady flow in pipelines and pipe networks, and the conservation of mass reduces to the volumetric flow rate, $Q$,

$Q = AV$

where $A$ is the cross sectional of the pipe, and $V$ is the mean section velocity. Typical units for discharge is liters per second (lps), gallons per minute (gpm), cubic meters per second (cms), cubic feet per second (cfs), and million gallons per day (mgd).

The continuity equation in two cross-sections of a pipe as depicted in Fig. 1 is

$ A_1V_1 = A_2V_2 $

Junctions (nodes) are where two or more pipes join together. A three-pipe junction node with constant external demand is shown in Fig. 2.

The continuity equation for the junction node is \begin{equation} Q_1 - Q_2 - Q_3 - D = 0 \end{equation}

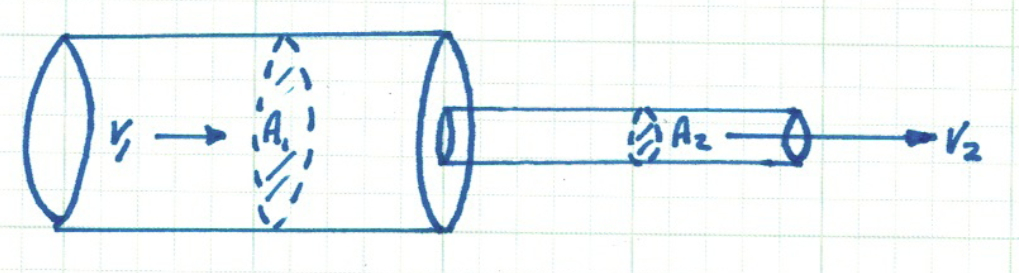
../../_images/continuity-across-sections.png

Fig. 1 Continuity of mass (discharge) across a change in cross section¶

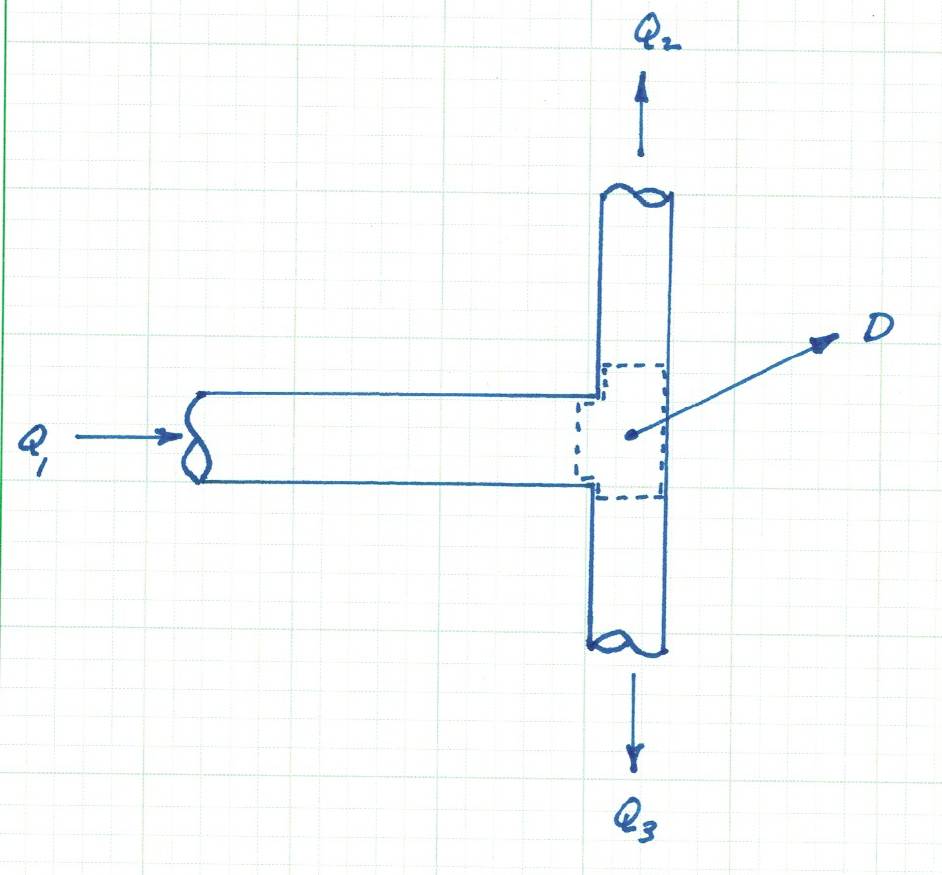
Fig. 2 Continuity of mass (discharge) across a node (junction)¶

In pipe network analysis, all demands on the system are stipulated to belocated at junctions (nodes), and the flow connecting junctions is assumed to be uniform across the cross sections (so that mean velocities apply). If a substantial demand is located between nodes, then an additional node is established at the demand location.

Energy Loss (along a link)¶

The equation below is the one-dimensional steady flow form of the energy equation typically applied for pressurized conduit hydraulics.

$ \begin{equation} \frac{p_1}{\rho g}+\alpha_1 \frac{V_1^2}{2g} + z_1 + h_p = \frac{p_2}{\rho g}+\alpha_2 \frac{V_2^2}{2g} + z_2 + h_t + h_l \label{eqn:closed-conduit-energy-equation} \end{equation} $

where $\frac{p}{\rho g}$ is the pressure head at a location, $\alpha \frac{V^2}{2g}$ is the velocity head at a location, $z$ is the elevation, $h_p$ is the added head from a pump, $h_t$ is the added head extracted by a turbine, and $h_l$ is the head loss between sections 1 and 2. Fig. 3 is a sketch that illustrates the various components in the energy equation.

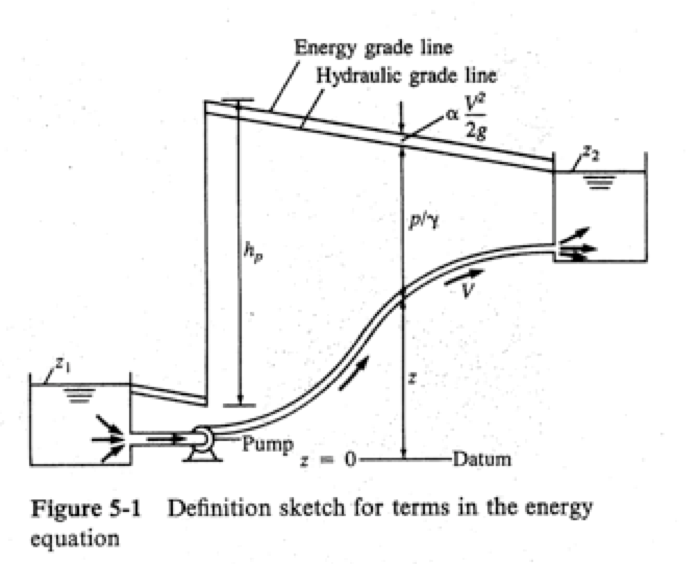
Fig. 3 Definition sketch for energy equation¶

In network analysis this energy equation is applied to a link that joins two nodes. Pumps and turbines would be treated as separate components (links) and their hydraulic behavior must be supplied using their respective pump/turbine curves.

Velocity Head¶

The velocity in $\alpha \frac{V^2}{2g}$ is the mean section velocity and is the ratio of discharge to flow area. The kinetic energy correction coefficient is $\begin{equation} \alpha=\frac{\int_A u^3 dA}{V^3 A} \label{eqn:kinetic-energy-correction} \end{equation} $ where $u$ is the point velocity in the cross section (usually measured relative to the centerline or the pipe wall; axial symmetry is assumed). Generally values of $\alpha$ are 2.0 if the flow is laminar, and approach unity (1.0) for turbulent flow. In most water distribution systems the flow is usually turbulent so $\alpha$ is assumed to be unity and the velocity head is simply $\frac{V^2}{2g}$.

Added Head — Pumps¶

The head supplied by a pump is related to the mechanical power supplied to the flow. Equation \ref{eqn:pump-power} is the relationship of mechanical power to added pump head. $ \begin{equation} \eta P=Q\rho g h_p \label{eqn:pump-power} \end{equation} $ where the power supplied to the motor is $P$ and the “wire-to-water” efficiency is $\eta$.

If the relationship is re-written in terms of added head(A negative head loss!} the pump curve is $ \begin{equation} h_p = \frac{\eta P}{Q\rho g} \label{eqn:pump-curve} \end{equation} $

This relationship illustrates that as discharge increases (for a fixed power) the added head decreases. Power scales at about the cube of discharge, so pump curves for computational application typically have a mathematical structure like $ \begin{equation} h_p = H_{\text{shutoff}} - K_{\text{pump}}Q^{\text{exponent}} \label{eqn:pump-curve-2} \end{equation} $

Extracted Head — Turbines¶

The head recovered by a turbine is also an “added head” but appears on the loss side of the equation.
The power that can be recovered by a turbine (again using the concept of “water-to-wire” efficiency is $ \begin{equation} P=\eta Q\rho g h_t \label{eqn:turbine-power} \end{equation} $

Pipe Head Loss Models¶

The Darcy-Weisbach, Chezy-Manning, and Hazen-Williams formulas are relationships between physical pipe characteristics, flow parameters, and head loss. The Darcy-Weisbach formula is the most consistent with the energy equation formulation being derivable (in structural form) from elementary principles (continunity and linear momentum), whereas the other two are empirical (despite the empirical nature of these two models all three are of practical use, and given a choice select your favorite!)

$ \begin{equation} h_{L_f}=f \frac{L}{D} \frac{V^2}{2g} \label{eqn:dw-headloss} \end{equation} $

where $h_{L_f}$ is the head loss from pipe friction, $f$ is a dimensionless friction factor, $L$ is the pipe length, $D$ is the pipe characteristic diameter, $V$ is the mean section velocity, and $g$ is the gravitational acceleration.

The friction factor, $f$, is a function of Reynolds number $Re_D$ and the roughness ratio $\frac{k_s}{D}$. $ \begin{equation} f=\sigma(Re_D,\frac{k_s}{D}) \label{eqn:friction-factor-dimensionless} \end{equation} $

The structure of $\sigma$ is determined experimentally. Over the last century the structure is generally accepted to be one of the following depending on flow conditions and pipe properties

Laminar flow (Eqn 2.36, pg. 17 Chin, D. (2006)) :¶

$\begin{equation} f=\frac{64}{Re_D} \label{eqn:friction-factor-laminar} \end{equation} $

Hydraulically Smooth Pipes(Eqn 2.34 pg. 16 Chin, D. (2006)):¶

$\begin{equation} \frac{1}{\sqrt{f}}=-2 log_{10} (\frac{2.51}{Re_d \sqrt{f} }) \label{eqn:friction-factor-smooth} \end{equation} $

Hydraulically Rough Pipes(Eqn 2.34 pg. 16 Chin, D. (2006)):¶

$ \begin{equation} \frac{1}{\sqrt{f}}=-2 log_{10} (\frac{\frac{k_e}{D}} {3.7}) \label{eqn:friction-factor-rough} \end{equation} $

Transitional Pipes (Colebrook-White Formula)(Eqn 2.35 pg. 17 Chin, D. (2006)):¶

$ \begin{equation} \frac{1}{\sqrt{f}}=-2 log_{10} (\frac{\frac{k_e}{D}} {3.7} + \frac{2.51}{Re_d \sqrt{f} } ) \label{eqn:friction-factor-CW} \end{equation} $

Transitional Pipes (Jain Formula)(Eqn 2.39 pg. 19 Chin, D. (2006)):¶

$\begin{equation} f=\frac{0.25}{[log_{10} (\frac{\frac{k_e}{D}} {3.7} + \frac{5.74}{Re_d^{0.9} } )] ^2} \label{eqn:friction-factor-Jain} \end{equation} $

Pipe Networks Solution Methods¶

Several methods are used to produce solutions (estimates of discharge, head loss, and pressure) in a network.
An early one, that only involves analysis of loops is the Hardy-Cross method.
A later one, more efficient, is a Newton-Raphson method that uses node equations to balance discharges and demands, and loop equations to balance head losses.

However, a rather ingenious method exists developed by Hamam, Y.M., and Brameller, A. (1971), where the flow distribution and head values are determined simultaneously. The task here is to outline the method on the problem below – first some necessary definitions and analysis.

The fundamental procedure is:

Continuity is written at nodes (node equations).
Energy loss (gain) is written along links (pipe equations).
The entire set of equations is solved simultaneously.

Network Analysis Example¶

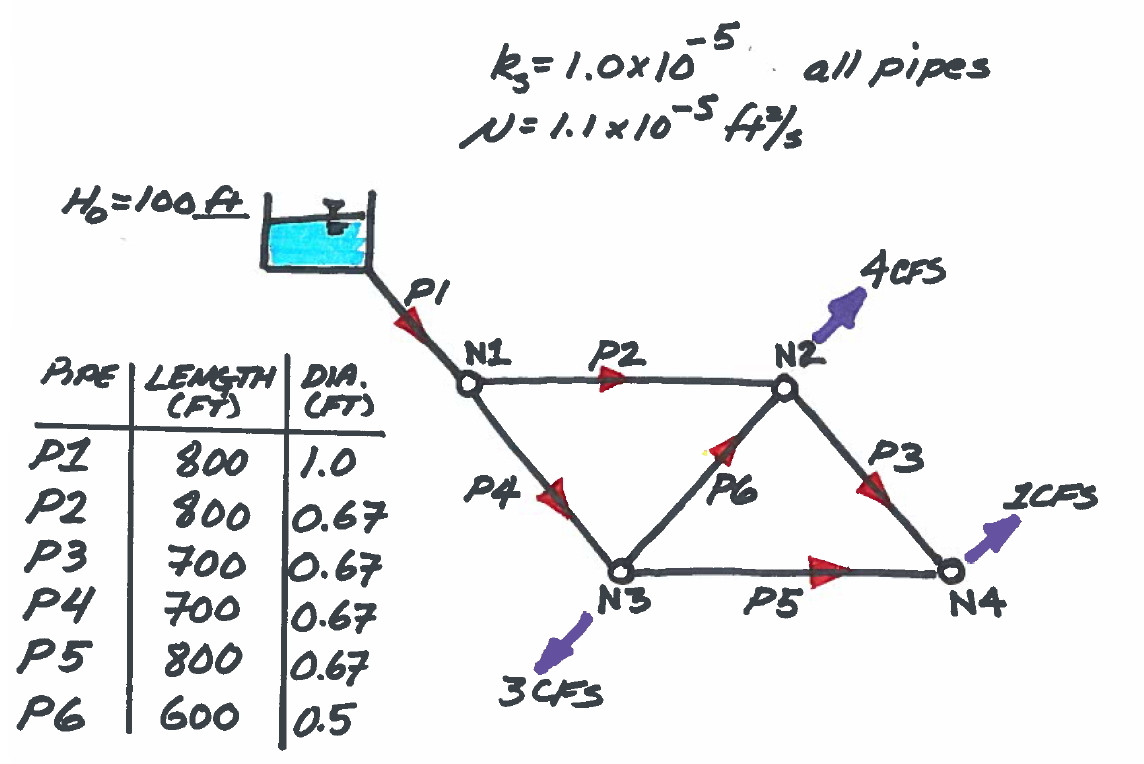
Fig. 4 Pipe network for illustrative example with supply and demands identified. Pipe dimensions and diameters are also depicted.¶

Fig. 4 is a sketch of the problem that will be used.
The network supply is the fixed-grade node in the upper left hand corner of the drawing.
The remaining nodes (N1 – N4) have demands specified as the purple outflow arrows. The pipes are labeled (P1 – P6), and the red arrows indicate a positive flow direction, that is, if the flow is in the indicated direction, the numerical value of flow (or velocity) in that link would be a positive number.

Define the flows in each pipe and the total head at each node as $Q_i$ and $H_i$ where the subscript indicates the particular component identification. Expressed as a vector, these unknowns are:

$ \begin{matrix} [Q_1, & Q_2, & Q_3, & Q_4, & Q_5, & Q_6, & H_1, & H_2, & H_3, &H_4 ]& = & \textbf{x} \\ \end{matrix} $

If we analyze continuity for each node we will have 4 equations (corresponding to each node) for continunity, for instance for Node N2 the equation is

$ \begin{matrix} ~& Q_2 & -Q_3 & ~ & ~ & Q_6 & ~ & ~ & ~ &~ & = & 4\\ \end{matrix} $

Similarily if we define head loss in any pipe as $\Delta H_i = f \frac{8 L_i}{\pi^2 g D_i^5} |Q_i| Q_i$ or $\Delta H_i = L_i Q_i$, where $L_i = f \frac{8 L_i}{\pi^2 g D_i^5} |Q_i|$, then we have 6 equations (corresponding to each pipe) for energy, for instance for Pipe (P2) the equation is:

$ \begin{matrix} ~& -L_2Q_2& ~ & ~ & ~ & ~& H_1 & -H_2 & ~ & ~ & = & 0\\ \end{matrix} $

If we now write all the node equations then all the pipe equations we could construct the following coefficient matrix below

Note

The horizontal lines divide the node and the pipe equations.

The upper partition are the node equations in Q and H, the lower partition are the pipe equations in Q and H}

$ \begin{matrix} \hline ~1&-1 & 0 & -1 & 0 & 0 & 0 & 0 & 0 &0 \\ 0&~1 & -1 & 0 & 0 &~1 & 0 & 0 & 0 &0 \\ 0& 0 & 0 &~1 & -1 & -1 & 0 & 0 & 0 &0 \\ 0& 0 &~1 & 0 &~1 & 0 & 0 & 0 & 0 &0 \\ \hline -L_1& 0& 0 & 0 & 0 & 0 & -1 & 0 & 0 &0 \\ 0& -L_2& 0 & 0 & 0 & 0&~1 & -1 & 0 &0 \\ 0& 0& -L_3 & 0 & 0 & 0& 0 &~1 & 0 & -1 \\ 0& 0& 0 & -L_4 & 0 & 0&~1 & 0 & -1 & 0 \\ 0& 0& 0 & 0 & -L_5 & 0& 0 & 0 &~1 & -1 \\ 0& 0& 0 &0 & 0 & -L_6& 0 & -1 &~1 & 0 \\ \hline \end{matrix} $

Declare the name of this matrix $\textbf{A(x)}$, where $\textbf{x}$ denotes the unknown vector of Q augmented by H as above. Next consider the right-hand-side at the correct solution (as of yet still unknown!) as

$ \begin{matrix} [0, & 4, & 3, & 1, & -100 , & 0, & 0, & 0, & 0, &0 ] = \textbf{b}\\ \end{matrix} $

So if the coefficient matrix is correct then the following system would result: $ \mathbf{A(x)} \cdot \mathbf{x} = \mathbf{b} $

which would look like

Fig. 5 Pipe network illustrative example as Matrtx-Vector system of equations.¶

Observe, the system is non-linear because the coefficient matrix depends on the current values of $Q_i$ for the $L_i$ terms. However, the system is full-rank (rows == columns) so it is a candidate for Newton-Raphson.

Further observe that the upper partition from column 6 and smaller is simply the node-arc incidence matrix, and the lower partition for the same columns only contains $L_i$ terms on its diagonal, the remainder is zero.
Next observe that the partition associated with heads in the node equations is the zero-matrix.

Lastly (and this is important!) the lower right partition is the transpose of the node-arc incidence matrix subjected to scalar multiplication of $-1$. The importance is that all the information needed to find a solution is contained in the node-arc incidence matrix and the right-hand-side – the engineer does not need to identify closed loops (nor does the computer need to find closed loops).

The trade-off is a much larger system of equations, however solving large systems is far easier that searching a directed graph to identify closed loops, furthermore we obtain the heads as part of the solution process.

Script Structure¶

The script will need to accomplish several tasks including reading the node-arc incidence matrix supplied as a file and convert the strings into numeric values. The script will also need some support functions defined before constructing the matrix. First the file for the example is:

PipeNetwork.txt

4
6
0 200.0 200.0 200.0 
00 0.67 0.67 0.67 0.67 0.5
800 700 700 800 600
00001 0.00001 0.00001 0.00001 0.00001 0.00001
000011
1 1 1 1 1
-1 0 -1 0 0
1 -1 0 0 1
0 0 1 -1 -1
0 1 0 1 0
4 3 1 -300 0 0 0 0 0 

The rows of the input file are:

The node count.
The pipe count.
Pipe diameters, in feet.
Pipe lengths, in feet.
Pipe roughness heights, in feet.
Kinematic viscosity in feet$^2$/second.
Initial guess of flow rates (unbalanced OK, non-zero vital!)
The next four rows are the node-arc incidence matrix.
The last row is the demand (and fixed-grade node total head) vector.

Support Functions¶

The Reynolds number will need to be calculated for each pipe at each iteration of the solution, so a Reynolds number function will be useful. For circular pipes, the following equation should work,

$Re_D=\frac{V_i \cdot D_i }{\mu}$

The Jain equation (Jain, 1976) that directly computes friction factor from Reynolds number, diameter, and roughness is

$f= \frac{0.25}{(log_{10}(\frac{\epsilon}{3.7D}+\frac{5.74}{Re_D^{0.9}}))^2}$

Once you have the Reynolds number for a pipe, and the friction factor, then the head loss factor that will be used in the coefficient matrix (and the Jacobian) is

$k_i = \frac{8 \cdot L_i}{\pi^2 g D_i^5}$

We will also find it handy to be able to compute velocity heads from discharge and pipe diameters so we can have a velocity function as

$V_i = \frac{Q_i}{0.25 \cdot \pi D_i^2}$

These support functions are coded below (in a code cell) as:

# hydraulic elements prototype functions
# Jain Friction Factor Function -- Tested OK 23SEP16
import math   # This will import math module

def friction_factor(roughness,diameter,reynolds):
    temp1 = roughness/(3.7*diameter)
    temp2 = 5.74/(reynolds**(0.9))
    temp3 = math.log10(temp1+temp2)
    temp3 = temp3**2
    friction_factor = 0.25/temp3
    return(friction_factor)

# Velocity Function
def velocity(diameter,discharge):
    velocity=discharge/(0.25*math.pi*diameter**2)
    return(velocity)

# Reynolds Number Function  
def reynolds_number(velocity,diameter,mu):
    reynolds_number = abs(velocity)*diameter/mu
    return(reynolds_number)

# Geometric factor function
def k_factor(howlong,diameter,gravity):
    k_factor = (16*howlong)/(2.0*gravity*math.pi**2*diameter**5)
    return(k_factor)

We will need our linear solver:

# SolveLinearSystem.py
# Code to read A and b
# Then solve Ax = b for x by Gaussian elimination with back substitution
#
##########
def linearsolver(A,b):
    n = len(A)
#    M = A  #this is object to object equivalence
# copy A into M element by element - to operate on M without destroying A
    M=[[0.0 for jcol in range(n)]for irow in range(n)]
    for irow in range(n):
        for jcol in range(n):
            M[irow][jcol]=A[irow][jcol]

#
    i = 0
    for x in M:
     x.append(b[i])
     i += 1

    for k in range(n):
     for i in range(k,n):
       if abs(M[i][k]) > abs(M[k][k]):
          M[k], M[i] = M[i],M[k]
       else:
          pass

     for j in range(k+1,n):
         q = float(M[j][k]) / M[k][k]
         for m in range(k, n+1):
            M[j][m] -=  q * M[k][m]

    x = [0 for i in range(n)]

    x[n-1] =float(M[n-1][n])/M[n-1][n-1]
    for i in range (n-1,-1,-1):
      z = 0
      for j in range(i+1,n):
          z = z  + float(M[i][j])*x[j]
      x[i] = float(M[i][n] - z)/M[i][i]
#    print (x)
    return(x)
#

We will also find some vector-matrix manipulation functions handy

def writeM(M,ir,jc,label):
    print ("------",label,"------")
    for i in range(0,ir,1):
        print (M[i][0:jc])
    print ("-----------------------------")
    return()

def writeV(V,ir,label):
    print ("------",label,"------")
    for i in range(0,ir,1):
        print (V[i])
    print ("-----------------------------")
    return()

def matrixmatrixmult(amatrix,bmatrix,rowNumA,colNumA,rowNumB,colNumB):
    AB =[[0.0 for j in range(colNumB)] for i in range(rowNumA)]
    for i in range(0,rowNumA):
        for j in range(0,colNumB):
            for k in range(0,colNumA):
                AB[i][j]=AB[i][j]+amatrix[i][k]*bmatrix[k][j]
    return(AB)

def matrixvectormult(amatrix,xvector,rowNumA,colNumA):
    bvector=[0.0 for i in range(rowNumA)]
    for i in range(0,rowNumA):
        for j in range(0,1):
            for k in range(0,colNumA):
                bvector[i]=bvector[i]+amatrix[i][k]*xvector[k]
    return(bvector)

def vectoradd(avector,bvector,length):
    cvector=[]
    for i in range(length):
        cvector.append(avector[i]+bvector[i])
    return(cvector)

def vectorsub(avector,bvector,length):
    cvector=[]
    for i in range(length):
        cvector.append(avector[i]-bvector[i])
    return(cvector)
             
def vdotv(avector,bvector,length):
    adotb=0.0
    for i in range(length):
        adotb=adotb+avector[i]*bvector[i]
    return(adotb)

Augmented and Jacobian Matrices¶

The $\textbf{A(x)}$ is built using the node-arc incidence matrix (which does not change), and the current values of $L_i$.
We also need to build the Jacobian of $\textbf{A(x)}$ to implement the update as-per Newton-Raphson.

A brief review; at the solution we can write $\begin{equation} [\mathbf{A}(\mathbf{x})] \cdot \mathbf{x} - \mathbf{b} = \mathbf{f}(\mathbf{x}) = \mathbf{0} \end{equation} $

Lets assume we are not at the solution, so we need a way to update the current value of $\textbf{x}$. Recall from Newton’s method (for univariate cases) that the update formula is

$ \begin{equation} x_{k+1}=x_{k} - (\frac{df}{dx}\mid_{x_k})^{-1} f(x_k) \end{equation} $

The Jacobian will play the role of the derivative, and $\textbf{x}$ is now a vector (instead of a single variable). Division is not defined for matrices, but the multiplicative inverse is (the inverse matrix), and plays the role of division. Hence, the extension to the pipeline case is

$ \begin{equation} \mathbf{x}_{k+1}=\mathbf{x}_{k} - [\mathbf{J}(\mathbf{x}_{k})]^{-1} \mathbf{f}(\mathbf{x}_k) \end{equation} $

where $\mathbf{J}(\mathbf{x}_{k})$ is the Jacobian of the coefficient matrix $\mathbf{A}$ evaluated at $\mathbf{x}_{k}$.
Although a bit cluttered, here is the formula for a single update step, with the matrix, demand vector, and the solution vector in their proper places.

$ \begin{equation} \mathbf{x}_{k+1}=\mathbf{x}_{k} - [\mathbf{J}(\mathbf{x}_{k})]^{-1} \{[\mathbf{A}(\mathbf{x}_k)] \cdot \mathbf{x}_k - \mathbf{b}\} \end{equation} $

As a practical matter we actually never invert the Jacobian, instead we solve the related Linear system of

$ [\mathbf{J}(\mathbf{x}_{k})] \cdot \Delta \mathbf{x} = \{[\mathbf{A}(\mathbf{x}_k)] \cdot \mathbf{x}_k - \mathbf{b}\} $

for $\Delta\textbf{x}$, then perform the update as $\textbf{x}_{k+1} = \textbf{x}_{k} - \Delta\textbf{x}$

Note

Inverting the matrix every step is computationally inefficient, and unnecessary. As an example, solving the system in this case would at worst take 10 row operations each step, but nearly 100 row operations to invert at each step – to accomplish the same result, generate an update. Now imagine when there are hundreds of nodes and pipes!

The Jacobian of the pipeline model is a matrix with the following properties:

The partition of the matrix that corresponds to the node formulas (upper left partition) is identical to the original coefficient matrix — it will be comprised of $0~\text{or}~\pm~1$ in the same pattern at the equivalent partition of the $\mathbf{A}$ matrix.
The partition of the matrix that corresponds to the pipe head loss terms (lower left partition), will consist of values that are twice the values of the coefficients in the original coefficient matrix (at any supplied value of $\mathbf{x}_k$.
The partition of the matrix that corresponds to the head terms (lower right partition), will consist of values that are identical to the original matrix.
The partition of the matrix that corresponds to the head coefficients in the node equations (upper right partition) will also remain unchanged.

We will want to take advantage of problem structure to build the Jacobian (you could just finite-difference the coefficient matrix to approximate the partial derivatives, but that is terribly inefficient if you already know the structure).

So now lets code reading the input file and building at least the starting instance of the matrix equations

First allocate some memory

bvector = []
rowNumA = 0
colNumA = 0
rowNumB = 0
verbose = 'false' # set to true for in-class demonstration
#############################################

elevation = [] # null list node elevations
diameter =  [] # null list pipe diameters
distance =  [] # null list pipe lengths
roughness = [] # null list pipe roughness
flowguess = [] # null list pipe flow rates
nodearcs =  [] # node-arc incidence matrix
rhs_true =  [] # null list for nodal demands
tempvect = []

Now read in the data from a file (useful to expand problem scale to many,many pipes and nodes).

##############################################
# connect and read file for Pipeline Network #
##############################################
afile = open("PipeNetwork.txt","r")
nnodes = int(afile.readline())
npipes = int(afile.readline())
# read elevation vector
tempvect.append([float(n) for n in afile.readline().strip().split()])
for i in range(0,nnodes,1):
    elevation.append(float(tempvect[0][i]))
tempvect = [] # reset vector
# read diameter vector
tempvect.append([float(n) for n in afile.readline().strip().split()])
for i in range(0,npipes,1):
    diameter.append(float(tempvect[0][i]))
tempvect = [] # reset vector
# read length vector
tempvect.append([float(n) for n in afile.readline().strip().split()])
for i in range(0,npipes,1):
    distance.append(float(tempvect[0][i]))
tempvect = [] # reset vector
# read roughness vector
tempvect.append([float(n) for n in afile.readline().strip().split()])
for i in range(0,npipes,1):
    roughness.append(float(tempvect[0][i]))
tempvect = [] # reset vector
# read viscosity (scalar)
viscosity = float(afile.readline())
# read current flow guess
tempvect.append([float(n) for n in afile.readline().strip().split()])
for i in range(0,npipes,1):
    flowguess.append(float(tempvect[0][i]))
tempvect = [] # reset vector
# read nodearc incidence matrix
## future revisions read directly into augmented matrix, or find way to release nodearc from stack
for irow in range(0,nnodes,1):  # then read each row
    nodearcs.append([float(n) for n in afile.readline().strip().split()])
# read demands guess
tempvect.append([float(n) for n in afile.readline().strip().split()])
for i in range(0,nnodes+npipes,1):
    rhs_true.append(float(tempvect[0][i]))
tempvect = [] # reset vector      
######################################
# end file read ,disconnect file     #
######################################
afile.close() # Disconnect the file

Echo the data just read, could put into a conditional and choose not to display except for debugging.

######################################
# echo the input in human readable   #
######################################
print('number of nodes : ',nnodes)
print('number of pipes : ',npipes)
print('viscosity       : ',viscosity)
print ("-----------------------------")
for irow in range(0,nnodes):
    print('node id:',irow, ', elevation :',elevation[irow],' head :',rhs_true[irow+npipes])
print ("-----------------------------")
for jcol in range(0,npipes):
    print('pipe id:',jcol,', diameter : ' ,diameter[jcol],', distance : ',distance[jcol],
          ', roughness : ',roughness[jcol],', flow  : ',flowguess[jcol])
print ("-----------------------------")
##for jcol in range(0,nnodes+npipes):
##    print('irow :',jcol,' RHS True :',rhs_true[jcol])
##print ("-----------------------------")
print("node-arc incidence matrix")
for i in range(0,nnodes,1):
    print (nodearcs[i][0:npipes])
print ("-----------------------------")

number of nodes :  4
number of pipes :  6
viscosity       :  1.1e-05
-----------------------------
node id: 0 , elevation : 200.0  head : 0.0
node id: 1 , elevation : 200.0  head : 0.0
node id: 2 , elevation : 200.0  head : 0.0
node id: 3 , elevation : 200.0  head : 0.0
-----------------------------
pipe id: 0 , diameter :  1.0 , distance :  800.0 , roughness :  1e-05 , flow  :  1.0
pipe id: 1 , diameter :  0.67 , distance :  800.0 , roughness :  1e-05 , flow  :  1.0
pipe id: 2 , diameter :  0.67 , distance :  700.0 , roughness :  1e-05 , flow  :  1.0
pipe id: 3 , diameter :  0.67 , distance :  700.0 , roughness :  1e-05 , flow  :  1.0
pipe id: 4 , diameter :  0.67 , distance :  800.0 , roughness :  1e-05 , flow  :  1.0
pipe id: 5 , diameter :  0.5 , distance :  600.0 , roughness :  1e-05 , flow  :  1.0
-----------------------------
node-arc incidence matrix
[1.0, -1.0, 0.0, -1.0, 0.0, 0.0]
[0.0, 1.0, -1.0, 0.0, 0.0, 1.0]
[0.0, 0.0, 0.0, 1.0, -1.0, -1.0]
[0.0, 0.0, 1.0, 0.0, 1.0, 0.0]
-----------------------------

Now create the augmented matrix using the structure of the problem.

# create augmented matrix
colNumA = npipes+nnodes
rowNumA = nnodes+npipes
augmentedMat = [] # null list to store augmented matrix

#######################################################################################
augmentedMat = [[0.0 for j in range(colNumA)]for i in range(rowNumA)] #fill with zeroes
#build upper left partition -- from nodearcs
for ir in range(0,nnodes):
    for jc in range (0,npipes):
        augmentedMat[ir][jc] = nodearcs[ir][jc]
istart=nnodes
iend=nnodes+npipes
jstart=npipes
jend=npipes+nnodes
for ir in range(istart,iend):
    for jc in range (jstart,jend):
        augmentedMat[ir][jc] = -1.0*nodearcs[jc-jstart][ir-istart] + 0.0
if verbose == 'true' :
    print("augmented matrix before loss factors")
    writeM(augmentedMat,rowNumA,colNumA,"augmented matrix")

Stopping Criteria, and Solution Report}¶

You will need some way to stop the process – the three most obvious (borrowed from Newton’s method) are:

Approaching the correct solution (e.g. $[\mathbf{A}(\mathbf{x})] \cdot \mathbf{x} - \mathbf{b} = \mathbf{f}(\mathbf{x}) = \mathbf{0}$).
Update vector is not changing (e.g. $\mathbf{x}_{k+1}=\mathbf{x}_{k}$), so either have an answer, or the algorithm is stuck.
You have done a lot of iterations (say 100).

We want to have the script determine when to stop and report the conditions (which stopping criterion was used), and the values of flows and heads in the system.

Fisrt lets set some tolerances and an iteration limit, as well as allocate memory to store the auxiliary functions results

#######################################################################################
howmany=50 #iterations max
tolerance1 = 1e-24
tolerance2 = 1e-24
velocity_pipe = [0 for i in range(npipes)]  # null list velocities
reynolds      = [0 for i in range(npipes)]  # null list reynolds numbers
friction      = [0 for i in range(npipes)]  # null list friction 
geometry      = [0 for i in range(npipes)]  # null list geometry
lossfactor    = [0 for i in range(npipes)]  # null list loss
jacbMat = [] # null list to store jacobian matrix
jacbMat = [[0.0 for j in range(colNumA)]for i in range(rowNumA)] #fill with zeroes


solvecguess =[ 0.0 for i in range(rowNumA)] 
solvecnew =[ 0.0 for i in range(rowNumA)]
for i in range(0,npipes,1):
    solvecguess[i] = flowguess[i]
    geometry[i] = k_factor(distance[i],diameter[i],32.2)
#solvecguess is a current guess -- wonder if more pythonic way for this assignment
##    print('irow :',i,' Geometry Factor :',geometry[i])
##print ("-----------------------------")

And finally the money shot; where we wrap everything into a for loop to iteratively find a solution

###############################################################
## ITERATION LOOP                                             #
###############################################################
for iteration in range(howmany): # iteration outer loop
    if verbose == 'true' :
        print("solutions at begin of iteration",iteration)
        for jcol in range(0,nnodes+npipes):
            print('irow :',jcol,' solvecnew :',solvecnew[jcol]," solvecguess ",solvecguess[jcol])
        print ("-----------------------------")
    for i in range(0,npipes,1):
        velocity_pipe[i] = velocity(diameter[i],flowguess[i])    
        reynolds[i]=reynolds_number(velocity_pipe[i],diameter[i],viscosity)
        friction[i]=friction_factor(roughness[i],diameter[i],reynolds[i])
        lossfactor[i]=friction[i]*geometry[i]*abs(flowguess[i])
    if verbose == 'true' :
        for jcol in range(0,npipes):
            print('pipe id:',jcol,', velocity : ' ,velocity_pipe[jcol],', reynolds : ',reynolds[jcol],
          ', friction : ',friction[jcol],', loss factor : ',lossfactor[jcol],'flow guess',flowguess[jcol])
################################################################
# BUILD AUGMENTED MATRIX CURRENT Q+H SOLUTION                  #
################################################################
    augmentedMat = [[0.0 for j in range(colNumA)]for i in range(rowNumA)] #fill with zeroes
    #build upper left partition -- from nodearcs
    for ir in range(0,nnodes):
        for jc in range (0,npipes):
            augmentedMat[ir][jc] = nodearcs[ir][jc]
    #build lower right == transpose of upper left
    istart=nnodes
    iend=nnodes+npipes
    jstart=npipes
    jend=npipes+nnodes
    for ir in range(istart,iend):
        for jc in range (jstart,jend):
            augmentedMat[ir][jc] = -1.0*nodearcs[jc-jstart][ir-istart] + 0.0
    # build lower left partition of the matrix
    istart = nnodes
    iend = nnodes+npipes
    jstart = 0
    jend = npipes
    for i in range(istart,iend ):
        for j in range(jstart,jend ):
    #        print('i =',i,'j=',j)
            if (i-istart) == j :
    #            print('i =',i,'j=',j)
                augmentedMat[i][j] = -1.0*lossfactor[j] + 0.0
    if verbose == 'true' :
        print("updated augmented matrix in iteration",iteration)
        writeM(augmentedMat,rowNumA,colNumA,"augmented matrix")
################################################################
# BUILD JACOBIAN MATRIX CURRENT Q+H SOLUTION                   #
################################################################        
    # now build current jacobian
    for i in range(rowNumA):
        for j in range(colNumA):
            jacbMat[i][j] = augmentedMat[i][j]
    # modify lower left partition
    istart = nnodes
    iend = nnodes+npipes
    jstart = 0
    jend = npipes
    for i in range(istart,iend ):
        for j in range(jstart,jend ):
    #        print('i =',i,'j=',j)
            if (i-istart) == j :
    #            print('i =',i,'j=',j)
                jacbMat[i][j] = 2.0*jacbMat[i][j]
##        for jcol in range(0,nnodes+npipes):
##            print('irow :',jcol,' solvecnew :',solvecnew[jcol]," solvecguess ",solvecguess[jcol])
##        print ("-----------------------------")
# matrix multiply augmentedMat*solvecguess to get current g(Q)
#    gq = [0.0 for i in range(rowNumA)] # zero gradient vector
##    if verbose == 'true' :
##        print("augmented matrix in iteration",iteration)
##        writeM(augmentedMat,rowNumA,colNumA,"augmented matrix before mmult")
    gq = matrixvectormult(augmentedMat,solvecguess,rowNumA,colNumA)
##    if verbose == 'true' :
##        writeV(gq,rowNumA,"gq vectorbefore subtract rhs_true")
# subtract rhs
#    for i in range(rowNumA):
    gq = vectorsub(gq,rhs_true,rowNumA)#vector subtract
    if verbose == 'true' :
        print("computed g(q) in iteration",iteration)
        writeV(gq,rowNumA,"gq vector")
        print("compare current and new guess")
        for jcol in range(0,nnodes+npipes):
            print('irow :',jcol,' solvecnew :',solvecnew[jcol]," solvecguess ",solvecguess[jcol])
        print ("-----------------------------")
    dq = [0.0 for i in range(rowNumA)] # zero update vector
    if verbose == 'true' :
        writeV(dq,rowNumA,"dq vector before linear solve")
    if verbose == 'true' :
        print("jacobian before linearsolve in iteration",iteration)
        writeM(jacbMat,rowNumA,colNumA,"jabobian matrix")
    dq = linearsolver(jacbMat,gq) # memory leak after this call - linearsolve clobbers input lists
#    dq = np.linalg.solve(jacbMat,gq)
    if verbose == 'true' :
        print("jacobian after linearsolve in iteration",iteration)
        writeM(jacbMat,rowNumA,colNumA,"jabobian matrix")

    if verbose == 'true' :
        writeV(dq,rowNumA,"dq vector -after linear solve")
    solvecnew = vectorsub(solvecguess,dq,rowNumA)#vector subtract
    if verbose == 'true' :
        print("Q_new = Q_old - DQ")
        writeV(solvecnew,rowNumA,"new guess vector")
#    tempvect =[ 0.0 for i in range(rowNumA)]
##        tempvect = matrixvectormult(jacbMat,dq,rowNumA,colNumA)
##        writeV(tempvect,rowNumA,"J*dq vector")
##        tempvect = vectorsub(tempvect,gq,rowNumA)
##        writeV(tempvect,rowNumA,"J*dq - gq vector")
        print("just after computing new guess, should be different")
        for jcol in range(0,nnodes+npipes):
            print('irow :',jcol,' solvecnew :',solvecnew[jcol]," solvecguess ",solvecguess[jcol])
        print ("-----------------------------")
#test for stopping
    tempvect =[ 0.0 for i in range(rowNumA)]
    for i in range(rowNumA):
        tempvect[i] = abs(solvecnew[i] - solvecguess[i])
    test1 = vdotv(tempvect,tempvect,rowNumA)
    if verbose == 'true' :
        print('test1',test1)
    tempvect =[ 0.0 for i in range(rowNumA)]
    for i in range(rowNumA):
        tempvect[i] = abs(gq[i])
    test2 = vdotv(tempvect,tempvect,rowNumA)
    if verbose == 'true' :
        print('test2',test2)
    if test1 < tolerance1 :
        print("update not changing --exit and report current update")
        print("iteration",iteration)
# update guess
        solvecguess[:] = solvecnew[:]
        for i in range(0,npipes,1):
            flowguess[i] = solvecguess[i]

        break
    if test2 < tolerance2 :
        print("gradient near zero --exit and report current update")
        print("iteration",iteration)
# update guess
        solvecguess[:] = solvecnew[:]
        for i in range(0,npipes,1):
            flowguess[i] = solvecguess[i]

        break
    if verbose == 'true' :
        print("solution continuing")
        print("iteration",iteration)
    # update guess
    solvecguess[:] = solvecnew[:]
    if verbose == 'true' :
        for i in range(0,npipes,1):
            flowguess[i] = solvecguess[i]
## Write Current State ######################
        gq = matrixvectormult(augmentedMat,solvecguess,rowNumA,colNumA)
        print('number of nodes : ',nnodes)
        print('number of pipes : ',npipes)
        print('viscosity       : ',viscosity)
        print ("-----------------------------")
        for irow in range(0,nnodes):
            print('node id:',irow, ', elevation :',elevation[irow])
        print ("-----------------------------")
        for jcol in range(0,npipes):
            print('pipe id:',jcol,', diameter : ' ,diameter[jcol],', distance : ',distance[jcol],
          ', roughness : ',roughness[jcol],', flow guess : ',round(flowguess[jcol],3))
        print ("-----------------------------")
        for jcol in range(0,nnodes+npipes):
            print('irow :',jcol,' RHS True :',rhs_true[jcol],"RHS Current",round(gq[jcol],3))
        print ("-----------------------------")
        for jcol in range(0,nnodes+npipes):
            print('irow :',jcol,' solvecnew :',solvecnew[jcol]," solvecguess ",solvecguess[jcol])
        print ("-----------------------------")   
################################################
# end of outer loop

update not changing --exit and report current update
iteration 39

Finally write the results and exit the process

print("results at iteration = :",iteration)
for i in range(0,npipes,1):
    flowguess[i] = solvecguess[i]
print('number of nodes : ',nnodes)
print('number of pipes : ',npipes)
print('viscosity       : ',viscosity)
print ("-----------------------------")
istart = int(npipes)
for irow in range(0,nnodes):
    print('node id:',irow, ', elevation :',elevation[irow],' head :',round(solvecnew[irow+npipes],3))
print ("-----------------------------")
for jcol in range(0,npipes):
    print('pipe id:',jcol,', diameter : ' ,diameter[jcol],', distance : ',distance[jcol],
  ', roughness : ',roughness[jcol],', flow  : ',round(flowguess[jcol],3))
print ("-----------------------------")
if verbose == 'true' :
    for jcol in range(0,nnodes+npipes):
        print('irow :',jcol,' RHS True :',rhs_true[jcol],"RHS Current",gq[jcol])
    print ("-----------------------------")
    for jcol in range(0,nnodes+npipes):
        print('irow :',jcol,' solvecnew :',solvecnew[jcol]," solvecguess ",solvecguess[jcol])
    print ("-----------------------------")

results at iteration = : 39
number of nodes :  4
number of pipes :  6
viscosity       :  1.1e-05
-----------------------------
node id: 0 , elevation : 200.0  head : 297.197
node id: 1 , elevation : 200.0  head : 287.489
node id: 2 , elevation : 200.0  head : 288.871
node id: 3 , elevation : 200.0  head : 287.013
-----------------------------
pipe id: 0 , diameter :  1.0 , distance :  800.0 , roughness :  1e-05 , flow  :  8.0
pipe id: 1 , diameter :  0.67 , distance :  800.0 , roughness :  1e-05 , flow  :  4.04
pipe id: 2 , diameter :  0.67 , distance :  700.0 , roughness :  1e-05 , flow  :  0.227
pipe id: 3 , diameter :  0.67 , distance :  700.0 , roughness :  1e-05 , flow  :  3.96
pipe id: 4 , diameter :  0.67 , distance :  800.0 , roughness :  1e-05 , flow  :  0.773
pipe id: 5 , diameter :  0.5 , distance :  600.0 , roughness :  1e-05 , flow  :  0.187
-----------------------------

Exercise 1:¶

Fig. 6 is a five-pipe network with a water supply source at Node 1, and demands at Nodes 1-4. The pipe dimensions are shown in the figure.

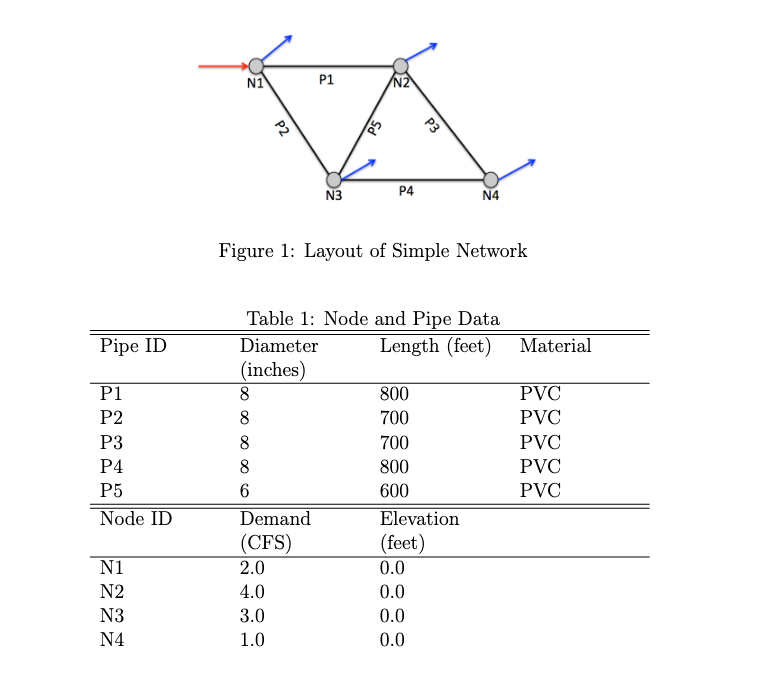
Fig. 6 Pipe network for¶

Make a table that lists each node name, node elevation, and the resultant pressure in U.S. Customary units.
Make a table that lists each pipe name, length, diameter, roughness height, and the resultant flow rate in U.S. Customary units.
Determine the flow rate in each pipe of the network, for the case where the total head at Node 1 is 100 feet.
Determine the Darcy-Weisbach friction factor in each pipe of the network.
Using the results of your flow distribution, determine the head loss from Node 1 to Node 4.
Determine the head at Node 4
Identify the node with the lowest pressure in your solution.

Exercise 2 (Advanced; optional)¶

Modify the algorithm and script to replace Pipe 1 in the lesson example Fig. 4 with a pump with the following pump curve.

$\begin{equation} h_p = H_{\text{shutoff}} - K_{pump}Q^2 \end{equation} $

Starting with values of shutoff head (116’) and a pump constant (0.05) and exponent (2) to supply water to the nodes; assume the supply node is as shown and all the nodes are at elevation 100’ (thus the pump must lift 100’).

Now to repeat the analysis using EPANET¶

Hardware Requirements¶

Running EPANET on a Mac¶

There are several ways to run PC programs on a Mac

Bootcamp and WindowsOS (Cost is ~190 USD at time of writing for the Windows OS)
Parallels and WindowsOS (Cost is ~80 USD for Parallels Desktop and ~190 USD for the Windows OS - you will get several years of functionality with this configuration)
CrossOver(~60 USD at the time of this writing; it appears to be a perpetual license, but as Apple degrades the OS it will stop working at some point. I would anticipate several years of useability)

What is presented below is a one-time Hack to get a running EPANET instance on your Macintosh. It is somewhat clumsy, because you will re-use a 3-rd Party Trial Software, and a base archive I have built for this class.

Long term you are better off with a proper PC, or pay for the codeweavers.com architecture translator

A hack you can use for this class leverages the codeweavers.com free-trial and its archiving function.

Note

I am using a paid-for CrossOver license to generate the “trial copies” and storing them on a server for you to download. This approach allows you to reset the trial period (by deleting and downloading). Be sure to save your work to your file system if you use this method.

Running EPANET on Amazon Web Services¶

A shared AWS instance is available for this course for learning how to use EPANET, accessed using Remote Desktop Protocol . If you have a Windows PC, you are way better off to simply install EPANET onto your computer and not use the cloud resource; if you have a Mac and are incapable of using one of the above virtualization solutions, then give the AWS instance a try.

Activate a RDP client for your computer

Linux is a bit complicated. The link has useable instructions.
Mac is simple, get RDP client from Microsoft or Apple Store (free)
The client is already built into the Windows OS, so nothing further to do here.

Once the client is activated connect to:

Server: kittyinthewindow.ddns.net
User: ce3372-share
Passwd: vnc#3372$1

The connection is a minimal performance Windows virtual machine. Move files using email and the supplied web-browser (Firefox).

Example (Repeated)¶

Start AWS (Optional)¶

Here we will use the AWS as the host:

So make the connection first using RDP

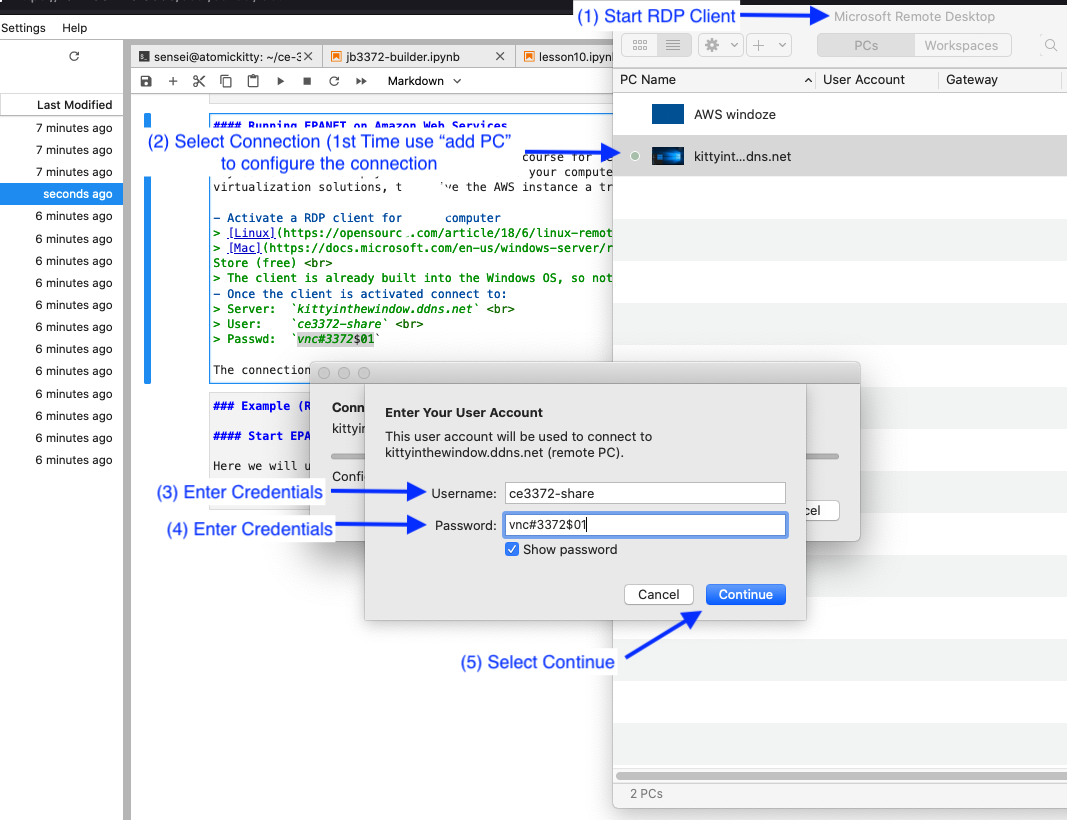
Fig. 7 RDP Connection to AWS Shared Desktop¶

Accept the security warning (the AWS instance cannot create a proper CA Certificate because it (the server) only exists after the connection is made, so the warning is normal)

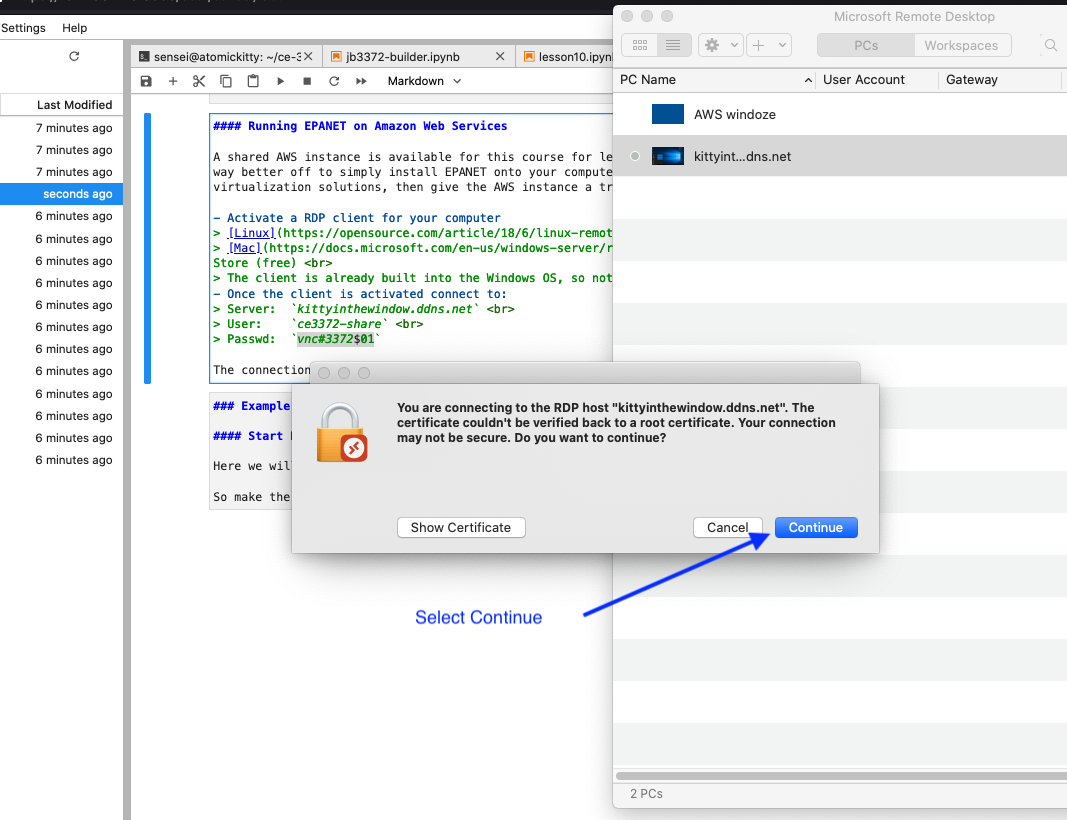
Fig. 8 RDP Connection to AWS Shared Desktop (Certificate Warning)¶

Wait awhile and viola! a remote connection to a Windoze-like machine.

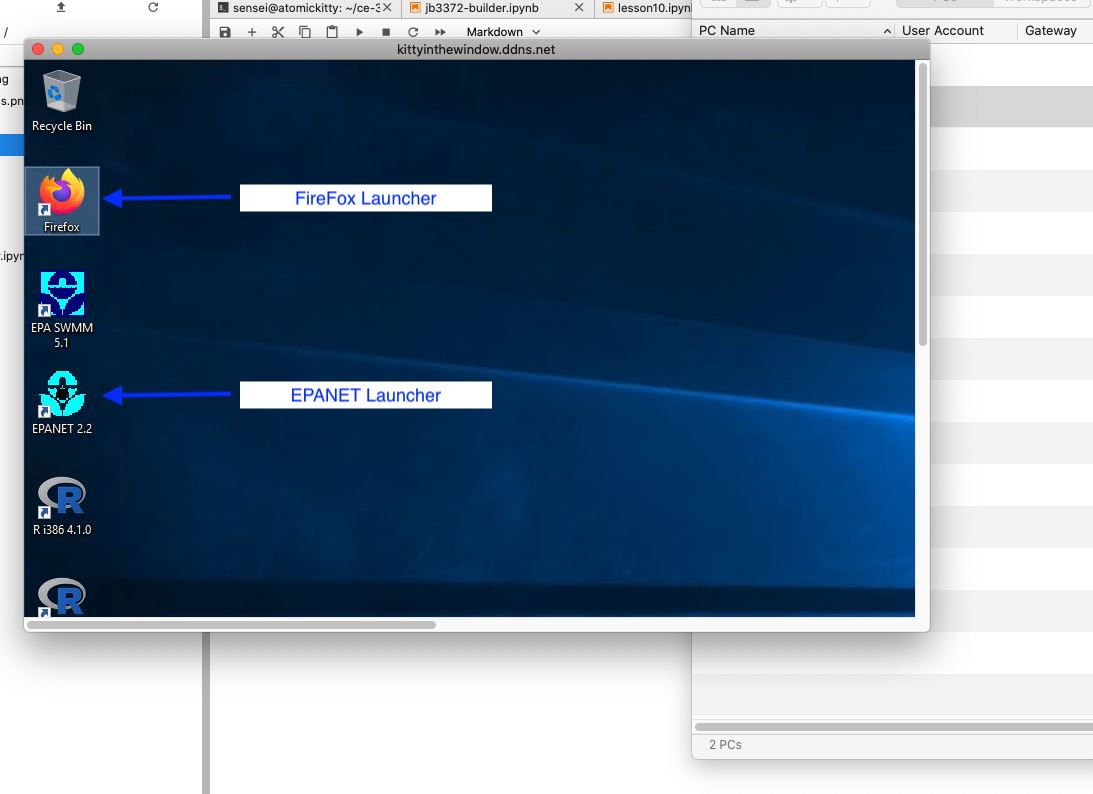
Fig. 9 AWS Shared Desktop¶

Start EPANET¶

Select the EPANET launcher to start the GUI, place and label the nodes

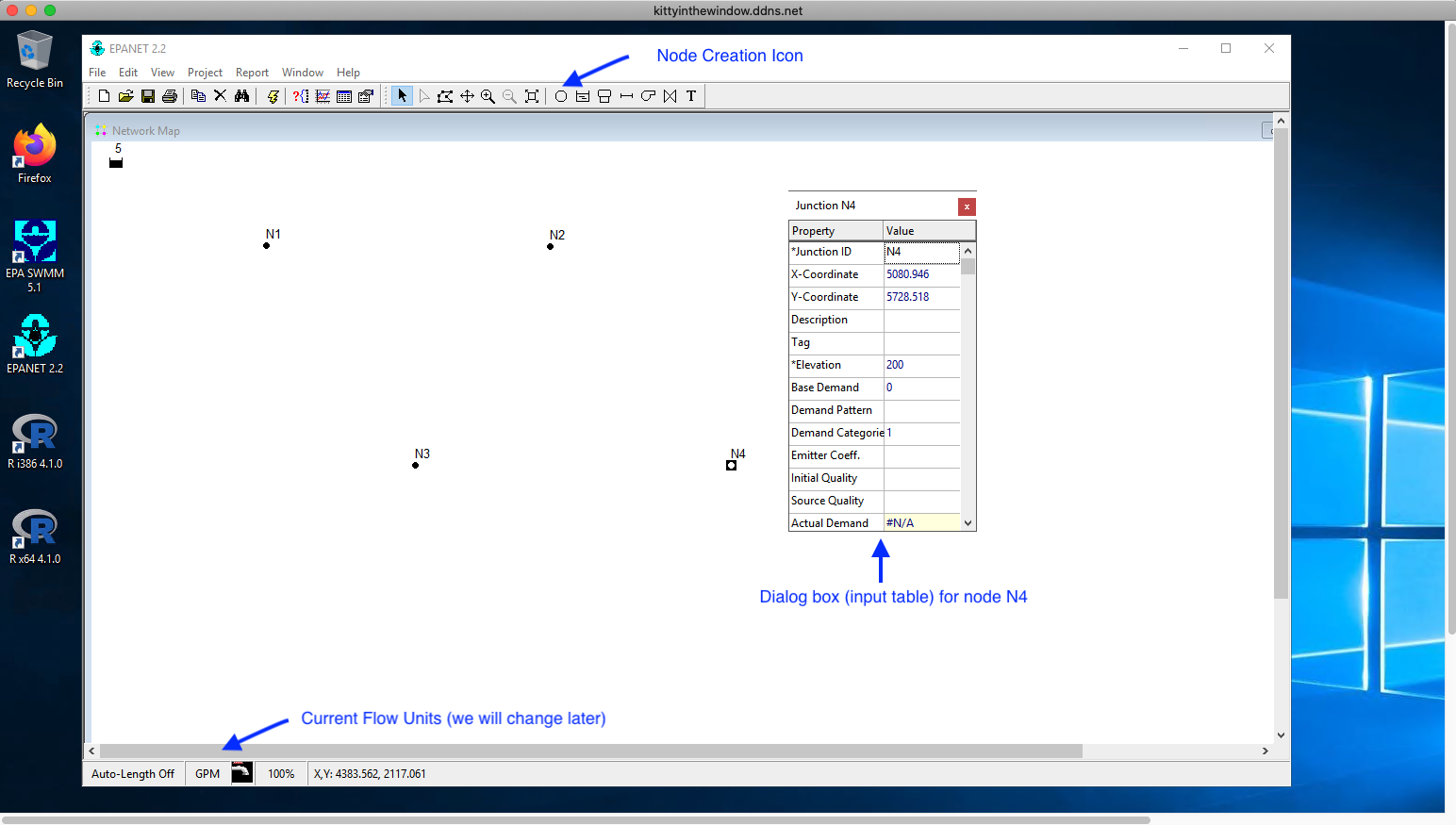
Fig. 10 Start EPANET, place nodes and reservoir, add labels and set elevations and set demands (in dialogs for each node)¶

Next place the pipes and insert the known values into the GUI

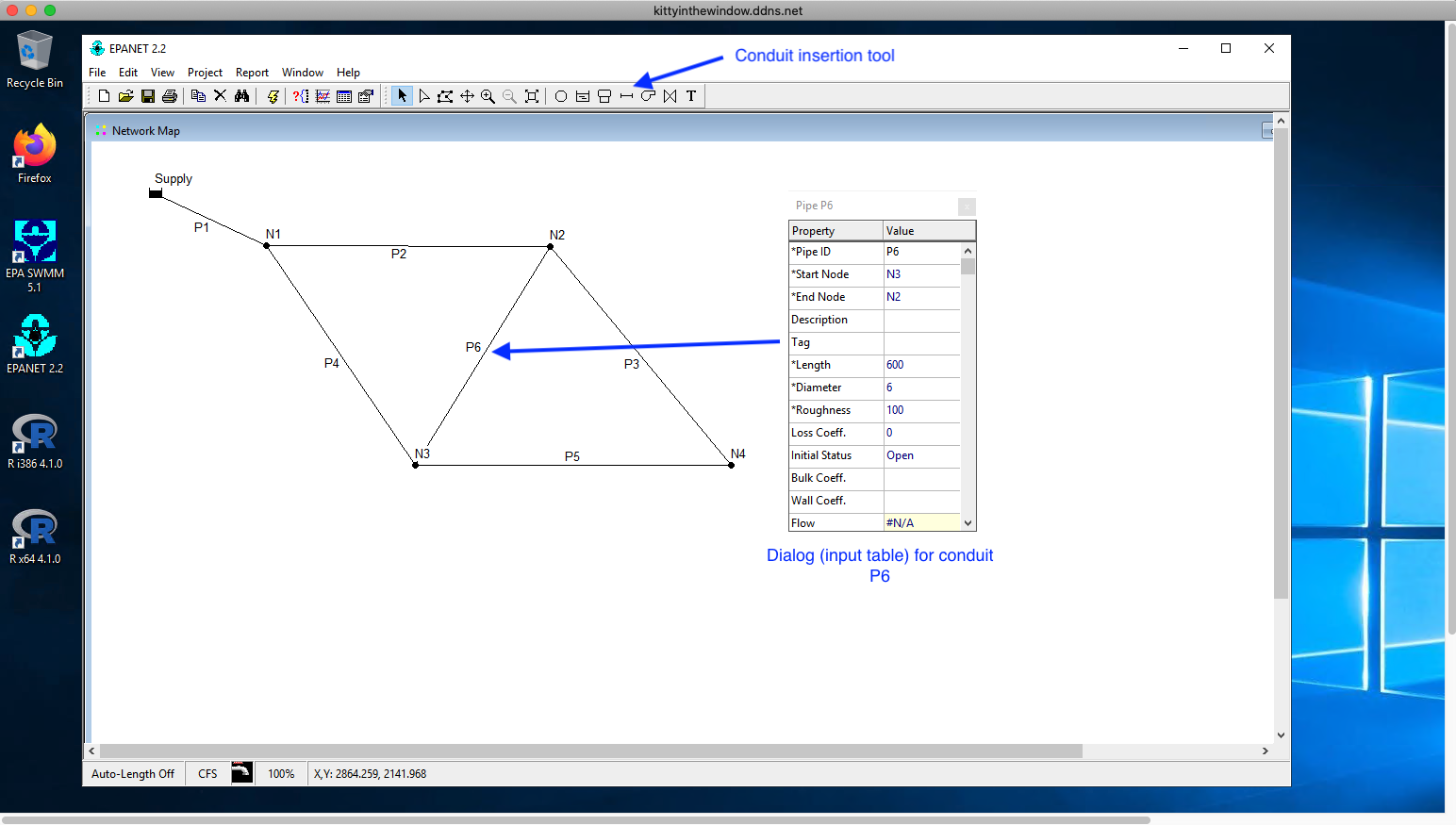
Fig. 11 Connect nodes and reservoir using pipes, add labels and set lengths and diameters (in dialogs for each node)¶

Next set the flow units, head loss model in the Project menu

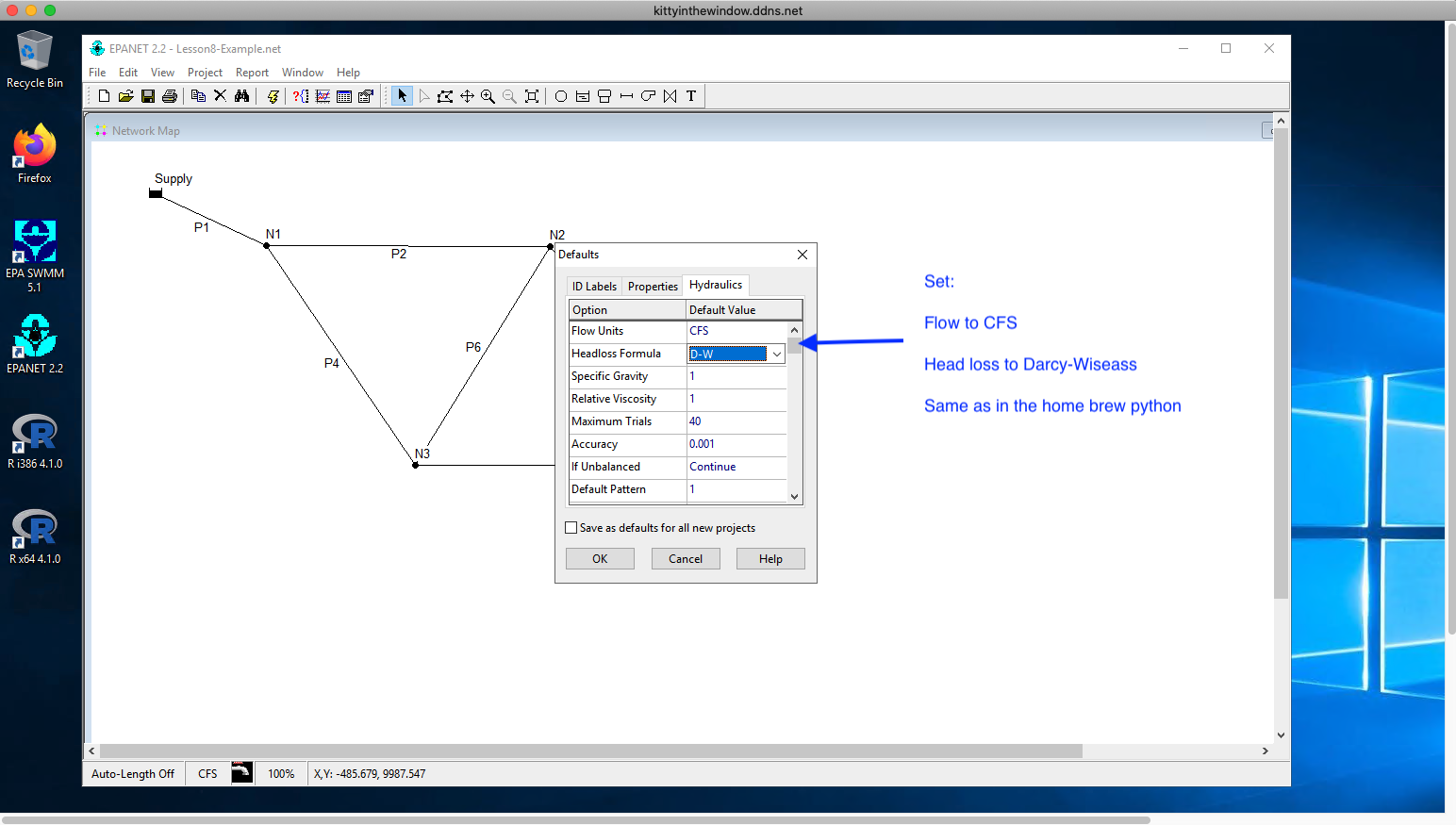
Fig. 12 In Menu/Project/Defaults/Hydraulics select flow units and headloss model¶

Now are ready to run the simulation,

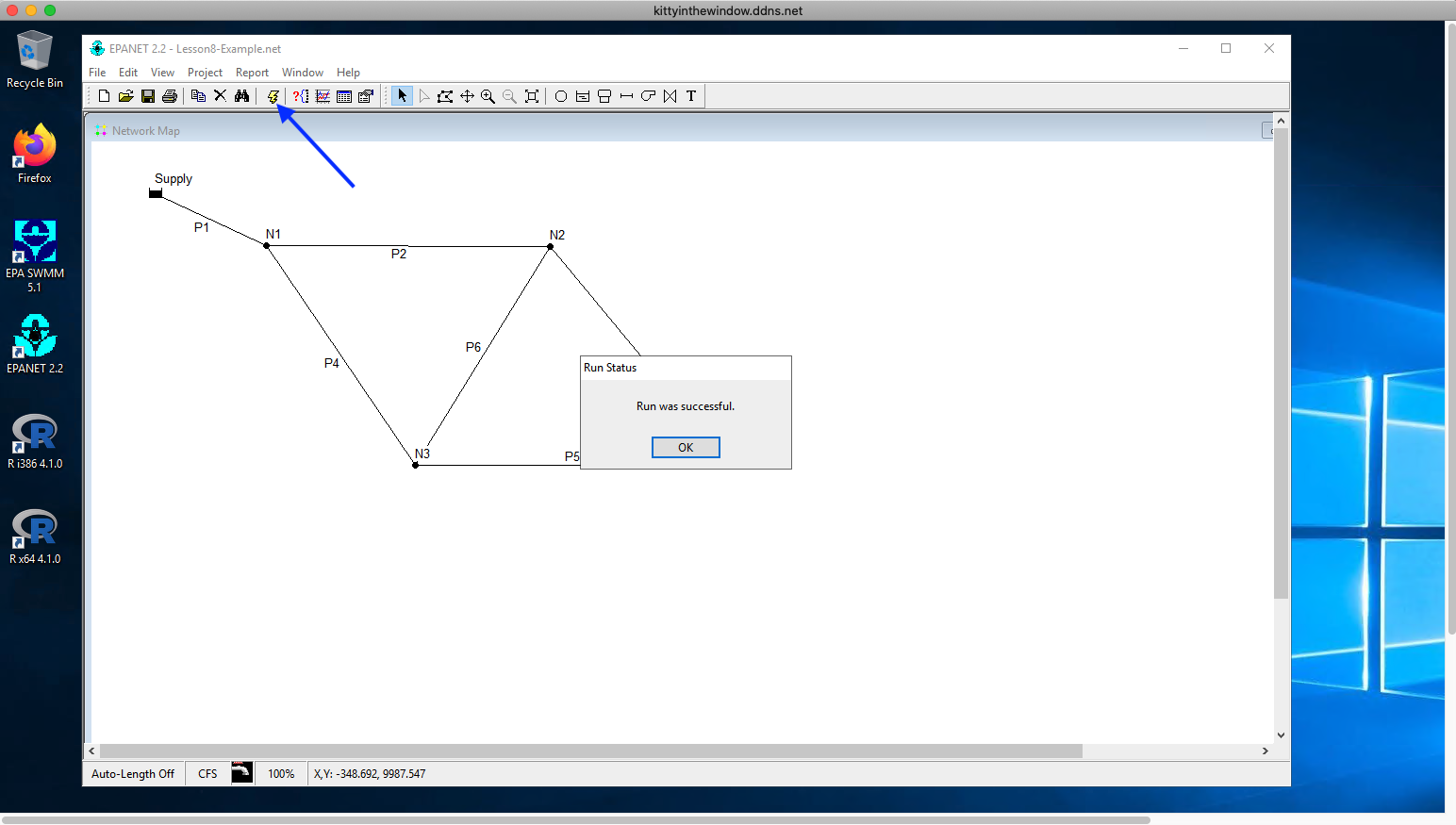
Fig. 13 In Menu/Project/Run Analysis or Select the Lightning Strike to run a simulation¶

Now we can interpret the results. The next figure has flow and pressure displayed at pipes and nodes. Select these using the Browser tool and View/Options in the menu.

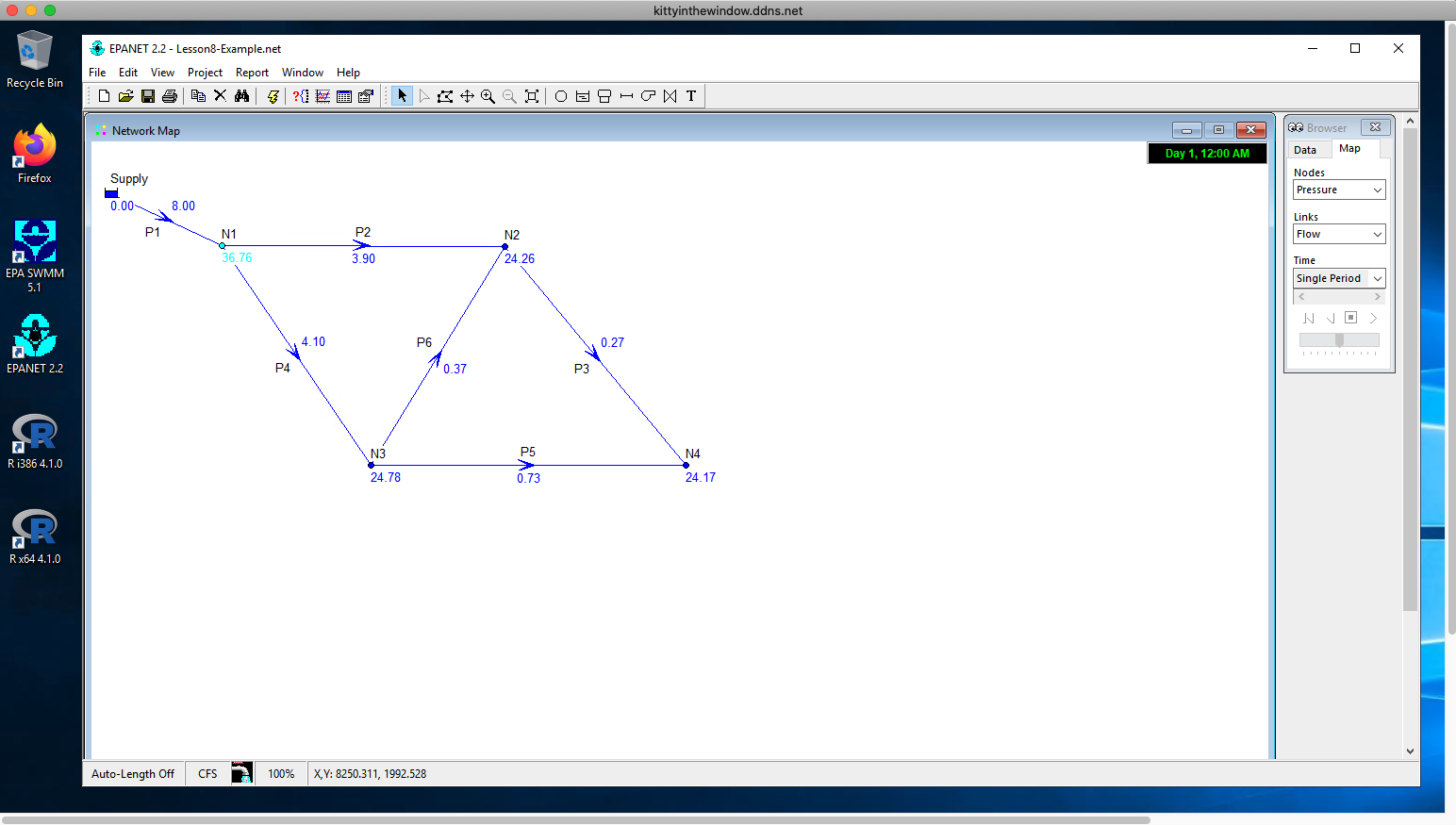
Fig. 14 Completed Example¶

Examination of the EPANET model and the homebrew code reveals nearly identical results, obviously EPANET is far easier for model development.

The example is saved on the AWS host as Lesson8-Example.net

Readings¶

Cleveland, T. G. (2015) Water Systems Design Notes to Accompany CE 3372 at TTU, Department of Civil, Environmental, and Construction Engineering, Whitacre College of Engineering. http://54.243.252.9/ce-3372-webroot/1-Lessons/Lesson08/PowerPointInLecture/CE3372-Lesson-8.key.pdf
Hydraulics of Pipelines and Pipe Networks Wurbs, R.A., and James, W. P. (2002) Water Resources Engineering, Prentice Hall; pp.130-156; and 156-198. http://54.243.252.9/ce-3372-webroot/3-Readings/Wurbs130-198/
Pipe Networks Chin, D. (2006). pp. 27-48 in “Water Resources Engineering, 2 ed.” Prentice Hall, Inc. http://54.243.252.9/ce-3372-webroot/3-Readings/Chin_27-48/
Water Distribution Systems “Water Distribution Systems” in Land Development Handbook, Ed. S.O. Dewberry, Dewberry Inc., McGraw-Hill http://54.243.252.9/ce-3372-webroot/3-Readings/WaterDistributionSystems/
Hamam, Y.M., and Brameller, A. (1971) “Hybrid method for the solution of piping networks.” Proc. IEEE, Vol. 118, No. 11, pp 1607-1612. http://54.243.252.9/ce-3372-webroot/3-Readings/HamamAndBrameller/
Jeppson, R.W. (1977) Analysis of Flow in Pipe Networks, Ann Arbor Science pp. 115-129 http://54.243.252.9/ce-3372-webroot/3-Readings/NewtonRaphsonTheory/
Jeppson, R.W. (1977) Analysis of Flow in Pipe Networks, Ann Arbor Science pp. 53-69 http://54.243.252.9/ce-3372-webroot/3-Readings/FlowInPipeNetworks/
Roberson, J.A., Cassidy, J.J., and Chaudry, M.H. (1988) Closed Conduits in “Hydraulic Engineering.” Houghton Mifflin Co. pp. 240-310 http://54.243.252.9/ce-3372-webroot/3-Readings/Chapter5/
Cleveland, T. G. (2013) Water Systems Design Notes to Accompany CE 3372 at TTU, Department of Civil, Environmental, and Construction Engineering, Whitacre College of Engineering. http://54.243.252.9/ce-3372-webroot/3-Readings/HydraulicsNotes/
Computational Hydraulics in R (for CE 3305) http://54.243.252.9/ce-3372-webroot/3-Readings/CFMinR/
Yoo, D.H. and Singh V. P. (2005) Two Methods for the Computation of Commercial Pipe Friction Factors. ASCE Journal of Hydraulic Engineering, 2005, 131(8): 694-704 http://54.243.252.9/ce-3372-webroot/3-Readings/FrictionFactor/

CE 3372 Water Systems Design

Pipe Networks¶

Pipeline Network Simulation¶

Background: Pipelines and Networks¶

Pipe Networks – Topology¶

Continunity (at a node)¶

Energy Loss (along a link)¶

Velocity Head¶

Added Head — Pumps¶

Extracted Head — Turbines¶

Pipe Head Loss Models¶

Laminar flow (Eqn 2.36, pg. 17 Chin, D. (2006)) :¶

Hydraulically Smooth Pipes(Eqn 2.34 pg. 16 Chin, D. (2006)):¶

Hydraulically Rough Pipes(Eqn 2.34 pg. 16 Chin, D. (2006)):¶

Transitional Pipes (Colebrook-White Formula)(Eqn 2.35 pg. 17 Chin, D. (2006)):¶

Transitional Pipes (Jain Formula)(Eqn 2.39 pg. 19 Chin, D. (2006)):¶

Pipe Networks Solution Methods¶

Network Analysis Example¶

Script Structure¶

Support Functions¶

Augmented and Jacobian Matrices¶

Stopping Criteria, and Solution Report}¶

Exercise 1:¶

Exercise 2 (Advanced; optional)¶

Now to repeat the analysis using EPANET¶

Hardware Requirements¶

Running EPANET on a Mac¶

Running EPANET on Amazon Web Services¶

Example (Repeated)¶

Start AWS (Optional)¶

Start EPANET¶

Readings¶