Hydrologic Cycle#
The water, or hydrologic, cycle describes the journey of water as water molecules make their way from the Earth’s surface to the atmosphere and back again, in some cases to below the surface. This gigantic system, powered by energy from the Sun, is a continuous exchange of moisture between the oceans, the atmosphere, and the land. A typical diagram depicting the hydrologic cycle is shown below.
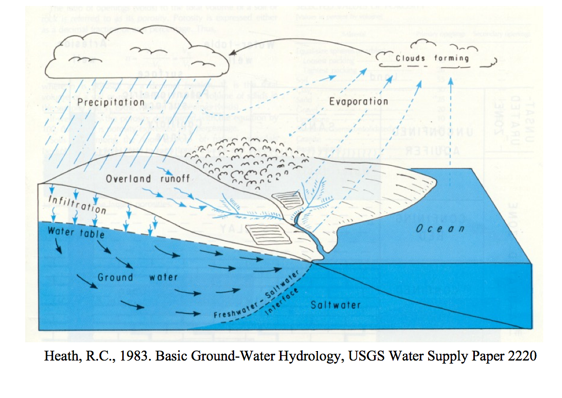
The driving force for the cycle is solar energy that provides the energy to vaporize liquid water that then rises into clouds, moves onshore, and rains (or snow, sleet, \(\dots\). and other forms of precipitation) A portion of the rain becomes runoff, another portion returns to the atmosphere as evaporation, another portion infiltrates into the ground and becomes groundwater.
A more detailed accounting of the precipitation is as follows:
A portion known as interception is retained on buildings, vegetation, and other surfaces that eventually evaporates - the remaining quantity is called effective precipitation
Note
Excess precipitation is a similar concept. When discussing rainfall-runoff processes using some model (i.e. unit hydrograph methods), the quantity that becomes runoff is called excess precipitation. The terms are frequently used interchangeably.
Some of the effective precipitation also evaporates directly.
Another portion of effective precipitation infiltrates into the ground - a portion of infiltrated water returns to the atmosphere via transpiration, the remainder either percolates deeper into the ground or is incorporated in the vegetative biomass.
The water that percolates deeper into the ground becomes recharge to the groundwater system, and may appear at some point as baseflow in streams.
If the precipitation exceeds the combined evaporation and infiltration puddles form in small depressions on the land surface - this is called depression storage.
After the depressions are filled they join and a continuous film of water can begin to flow over the surface to a stream channel. This portion that can flow is called the excess precipitation (see the note above), and the flow is called the direct runoff.
Runoff occurs when the film of water begins to move - water in this film is said to be in detention storage, and evaporation occurs from this compartment too. When precipitation ceases, the water in detention storage eventually joins the stream channel.
The destination of all streams is open bodies of water such as lakes, seas, and oceans which are subject to substantial evaporation.
The evaporation and tanspiration from all these sources combine and carry moisture back into the atmosphere which condenses and repeats the cycle.
Water Budget Definition#
The water budget, or hydrologic balance is simply the expression of the conservation of mass in hydrologic terms for a hydrologic system.
Generally it is expressed as a rate (or volume) balance.
The hydrologic equation is the fundamental tool in hydrology to describe amounts of water in storage in different compartments at different scales.
The equation expressed in “words” is
Rate of inflow - Rate of outflow = Rate of change of storage + Rate of internal mass generation.
Symbolically it is exrepssed as:
where
\(I\) is inflow volume, \(O\) is outflow volume, \(S\) is storage volume (i.e. within a watershed), and \(G\) is generated volume. \(G\) is generally zero, but is included to be consistent with the balance equations you have learned elsewhere (i.e. environmental engineering, chemistry, \(\dots\))
Water Budget Example 1#
Consider the following problem statement:

One way to answer the questions is to decompose the problem into a simpler construct, usually by sketching a diagram as shown below:
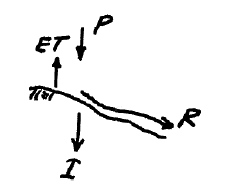
Now we can simply assign the terms to the appropriate parts of the water balance equation and solve for unknown components such as:

For more utility we can use our Computational Thinking (ENGR-1330) skills and write a simple script to generalize the results and help with unit conversions
# Water Budget Script - Example in WebBook
P = 254 # millimeters of rainfall
ET = 85 # millimeters of evapotranspiration
I = 20 # millimeters of infiltration
DeltaS = 0 # millimeters of storage change
R = P - ET - I + DeltaS
print("Runoff = ",round(R,3),' watershed millimeters')
Runoff = 149 watershed millimeters
Now to convert to other units as requested, we simply apply conversions as:
def mm2m(mm):
# convert mm into meters
mm2m = mm/1000.0 # mm should be a float
return(mm2m)
def sqkm2sqm(sqkm):
# convert square kilometers into square meters
sqkm2sqm = sqkm * 1.0e06 # sqkm should be a float
return(sqkm2sqm)
def cum2liter(cum):
# convert cubic meters into liters
cum2liter = cum*1000.0 # cum should be a float
return(cum2liter)
# now express result in useful units
area = 65 # area in sq. kilometers
WholeWatershedRunoff = mm2m(R)*sqkm2sqm(area)
print("Runoff = ",round(WholeWatershedRunoff,3),' cubic meters')
print("Runoff = ",round(cum2liter(WholeWatershedRunoff),3),' liters')
Runoff = 9685000.0 cubic meters
Runoff = 9685000000.0 liters
Now estimate largest population this hydrology could support
# Population supported at 160 L/day
litersPerDayPerPerson = 160
litersPer2months = litersPerDayPerPerson*2*30
# Assume all Runoff is Run through kidneys and colons
maxPeople = cum2liter(WholeWatershedRunoff)/litersPer2months
print("Maximum Population = ",maxPeople," if rainfall is firm")
Maximum Population = 1008854.1666666666 if rainfall is firm
Water Budget Example 2#
Consider the following problem statement:
At a particular time the storage in a river reach is 55.3 acre-ft. At that instant, the inflow to the reach is 375 cfs and the outflow is 563 cfs. Two hours later, the inflow the inflow to the reach is 600 cfs and the outflow is 675 cfs.
Estimate:
The change in storage over 2 hours.
The reach storage after 2 hours.
Solution:
Sketch the Situation#
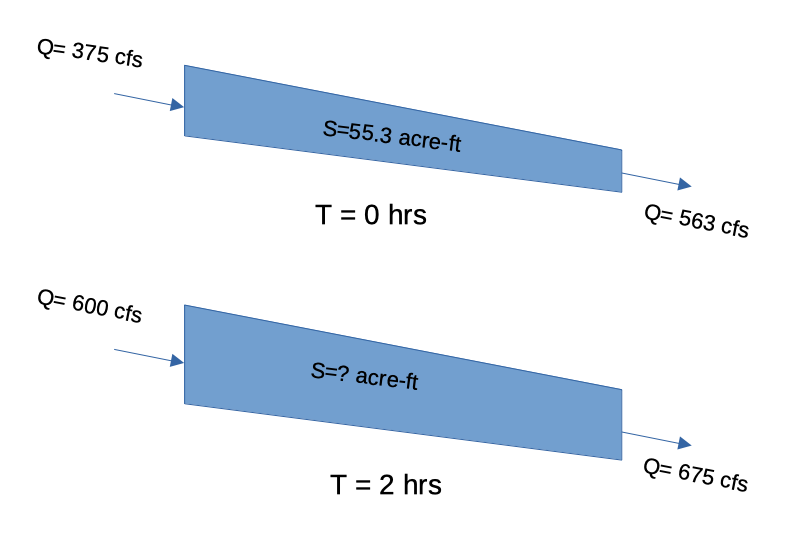
Governing Principles#
Apply the water balance model:
Analysis/Solution#
Observe that there is no internal mass generated, so that term will vanish. Discharge is changing over time, so we will have to choose how to cope with that, typically one chooses arithmetic means
Now we substitute into the equation and solve for the storage rate of change
Observe this is a rate! We will need to “integrate” to recover actual change
Now recover the estimated change in storage, and new storage value from the rate
A little unit conversion
Then apply definition of \(\frac{dS}{dt} \) as
So the new storage volume is
Now we can summarize the results
Value |
Amount |
Unit |
|---|---|---|
\(\Delta S\) |
-263 |
cfs-hr |
\(S_2\) |
33.57 |
acre-ft |
If we wish an ability to repeat such computations a lot (maybe we own the reach and want to charge our customers for water use) we could apply ENGR-1330 methods as below to explore different inflow and outflow conditions
# prototype function
def newS(t0,t1,I0,I1,O0,O1,S0):
Ibar = 0.5*(I0 + I1)
Obar = 0.5*(O0 + O1)
dsdt = Ibar - Obar
dsdt = dsdt*3600/43560 # convert to correct units
deltat = t1-t0
DS = dsdt*deltat
newS = S0+DS
return(newS)
# input values
t0 = 0 # hrs
t1 = 2 # hrs
I0 = 375 # cfs
I1 = 600 # cfs
O0 = 563 # cfs
O1 = 675 # cfs
S0 = 55.3 # acre-ft
# echo inputs
print("Begin Time",t0," hours")
print("End Time",t1," hours")
print("Inflow at Begin Time",I0," cfs")
print("Inflow at End Time",I1," cfs")
print("Outflow at Begin Time",O0," cfs")
print("Outflow at End Time",O1," cfs")
print("Storage at Begin Time",S0," acre-feet")
S1 = newS(t0,t1,I0,I1,O0,O1,S0) # get new storage
# output results
print("Storage at End Time",round(S1,2)," acre-feet")
Begin Time 0 hours
End Time 2 hours
Inflow at Begin Time 375 cfs
Inflow at End Time 600 cfs
Outflow at Begin Time 563 cfs
Outflow at End Time 675 cfs
Storage at Begin Time 55.3 acre-feet
Storage at End Time 33.56 acre-feet
