Problem 1.¶
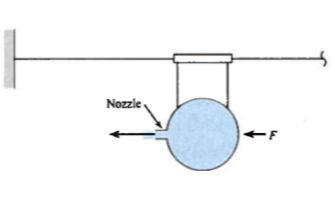
The figure is a schematic of a balloon rocket held in place by a force $F$.
The nozzle is a 0.8 $cm$ diameter tube, and an air jet exits the nozzle with a speed of 45 $m/s$ and a density of 1.2 $kg/m^3$.
Determine:
- The force $F$ needed to hold the balloon stationary.
# sketch here
# list known quantities
# list unknown quantities
# governing principles
# solution (step-by-step)
# discussion
Problem 2.¶
Below is a schematic of an elbow fitting in a pipe system.
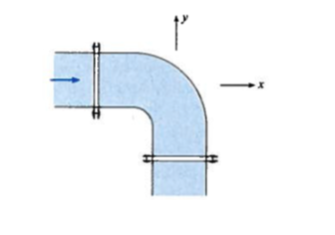
The gage pressure throughout the horizontal 90$^o$ bend (the elbow lies in the horizontal plane -- the figure is a plan view of the bend) is 300 $kPa$. The pipe diameter is 1 $m$ and the water (at 10 $^oC$) flow rate is 10 $m^3/s$
Determine:
- The $x-$component of force must be applied to the bend to hold in in place against the water action.
# sketch here
# list known quantities
# list unknown quantities
# governing principles
# solution (step-by-step)
# discussion
Problem 3.¶
Figure 2 is a schematic of a pumped-storage system. How much power must be supplied to the water by the pump (in kilowatts) to pump water at $0.085~m^3/s$ at 20$^o$C from the lower to the upper reservoir?
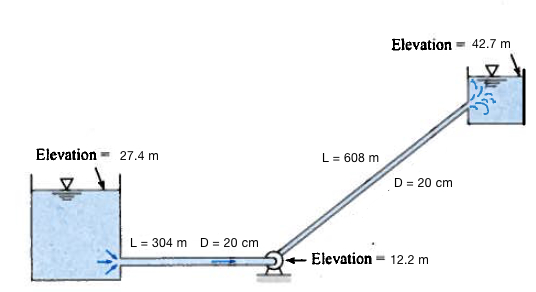
The head loss in the pipes is $h_l = 0.018 \frac{L}{D} \frac{V^2}{2g}$ , where $L$ is the length of the pipe in meters, and $D$ is the diameter of the pipe in meters.
Sketch the HGL and EGL for the system.
# sketch here
# list known quantities
# list unknown quantities
# governing principles
# solution (step-by-step)
# discussion
Problem 4.¶
Figure 1 is a schematic of a pipe with a series of holes used to sparge (introduce gas bubbles) gas into a larger volume.
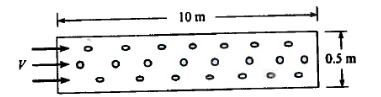
The volumetric flow rate through each hole depends on the pressure difference across the hole and is given by $$Q = 0.67A_0(\frac{2 \Delta p}{\rho})^{1/2} $$ where $A_0$ is the area of the hole, $\Delta p$ is the pressure difference across the hole, and $\rho$ is the density of gas in the pipe. If the pipe is sufficiently large, the pressure will be uniform along the pipe.
A distribution pipe for air at 20$^o~C$ is 0.5 meters in diameter and 10 m long. The gage pressure in the pipe is 100 Pa. The pressure outside the pipe is atmospheric at 1 bar. The hole diameter is 2.5 cm, and there are 50 holes per meter length of pipe. The pressure is constant in the pipe.
Determine
- The velocity of air entering the pipe
# sketch here
# list known quantities
# list unknown quantities
# governing principles
# solution (step-by-step)
# discussion
