Download (right-click, save target as ...) this page as a Jupyterlab notebook from: ES-1
CE 3305 Engineering Fluid Mechanics
Spring 2023 Exercise Set 1
LAST NAME, FIRST NAME
R00000000
Purpose :¶
Apply definition of density. Apply the ideal gas law under isothermal conditions. Use compressibility to relate pressure change to volume change.
Assessment Criteria :¶
Completion, results plausible, format correct, calculations (Jupyter Notebook) are shown.
Problem 1 (Problem 1-5 p. 32):¶
The tank contains a liquid with density of 1.22 $\frac{slug}{ft^3}$.
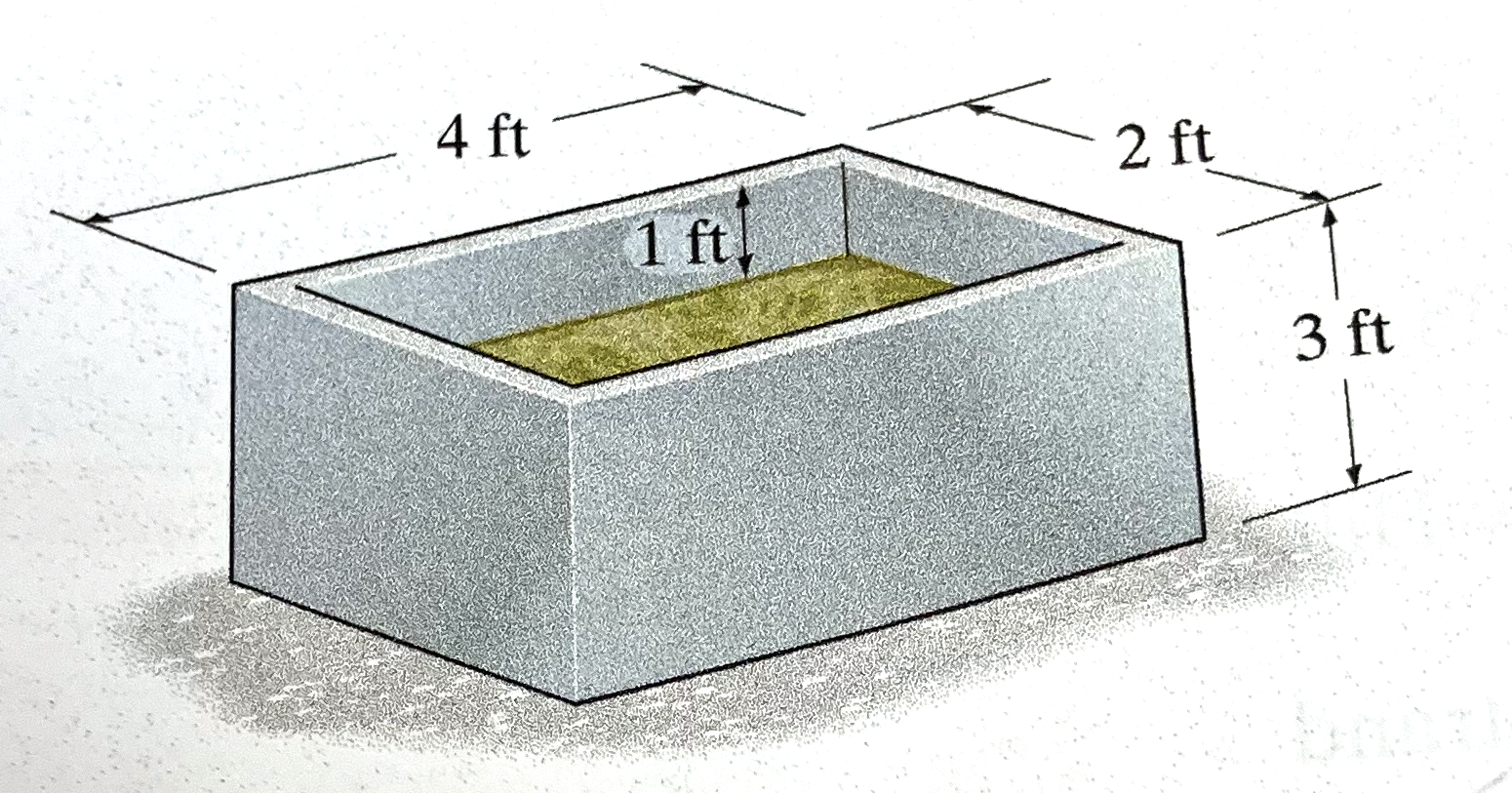
Determine:
- Weight (in pounds) of liquid when it is at level shown.
You may wish to use a Jupyter Notebook to create a script to handle the computations and show the results of the script. Upload your completed Notebook as a PDF to Blackboard. You can print the notebook to a PDF file, and upload that; if that method fails export the notebook as
HTMLthen use the on-line https://html2pdf.com/ converter
sketch
- Use above drawing; key is to note the 1-foot "freeboard" in the tank to obtain fluid bulk dimension
list known quantities
- liquid bulk dimension: 4 ft X 2 ft X (3-1)ft cubic feet
- liquid density : 1.22 $\frac{slug}{ft^3}$
list unknown quantities
- liquid weight (W=mg)
governing principles
- W = mg
- m = $\rho \times \text{volume}$
- volume = L $\times$ W $\times$ H
solution (step-by-step)
length = 4 #ft
width = 2 #ft
height = 3-1 #ft
volume = length*width*height
rho_l = 1.22 #slug/ft^3
mass = rho_l * volume
gravity = 32.2 #ft/s^2
weight = mass * gravity
print("Weight of : ",round(float(volume),0)," ft^3 of liquid is : ",round(weight,0)," pounds-force")
discussion
- Direct application of definition of mass density and weight as a force.
Problem 2 (Problem 1-7 pg. 32):¶
The tank has a volume of 0.35$m^3$ and contains 40 kg of nitrogen at a temperature of 40$^oC$.

Determine:
- Absolute pressure (in kPa) in the tank.
sketch here
- Use above sketch; tank dimensions not supplied, but T&V and mass are
list known quantities
- Temperature: 40 $^o$C
- Gas Volume: 0.35 $m^3$
- Gas Mass: 40 kg N$_2$ Need to be aware Nitrogen is diatomic in gas phase, so will adjust for 2-atom MW
list unknown quantities
- Pressure
governing principles
- Ideal gas law $pV = \frac{m}{MW} RT$
- MW Nitrogen is 14 g/mol, but diatomic gas will have 2 N atoms per mol.
- Ideal gas constant is 0.0821 L$\cdot$atm/K$\cdot$mol
solution (step-by-step)
R = 0.0821 #l-atm/K-mol
m = 40*1000 #grams - given
MW = 14*2 #grams/mol - diatomic gas
V = 0.35*1000 #liters
T = 40+273 #Kelvin
p = ((m/MW)*R*T)/V
print("Pressure in tank :",round(p,2)," atmospheres")
p = p*101.325
print("Pressure in tank :",round(p,2)," kiloPascals")
discussion
- Direct application of pvnrt-bong theory; convert atmospheres to kPa; note unusual (for engineering) units.
Problem 3 (Problem 1-18 pg. 33):¶
A solid has a specific weight of 310 lb/ft$^3$. When a pressure of 650 psi is applied the specific weight increases to 312 lb/ft$^3$.
Determine:
- Bulk modulus (of elasticity)
sketch here

Mass is constant, volume smaller as pressure bigger.
list known quantities
- $\Delta p $ = 650 psi
- $\gamma_1 $ = 310 lb/ft$^3$
- $\gamma_2 $ = 312 lb/ft$^3$
list unknown quantities
- $E_V$ bulk modulus of compressibility (eq. 1-11 in textbook)
governing principles
- $\gamma = \frac{W}{V}$
- $E_V = \frac{\Delta p}{-\frac{\Delta V}{V}}$
- $\frac{\Delta V}{V}=\frac{\frac{1}{\gamma_2} - \frac{1}{\gamma_1}}{\frac{1}{\gamma_1}}$
solution (step-by-step)
gamma1 = 310 #lb/ft^3
gamma2 = 312 #lb/ft^3
dpress = 650 #lb/in^2
dp = dpress*144 #lb/ft^2
dVoverV = ((1/gamma2)-(1/gamma1))/(1/gamma1)
bulkmodulus = -dp/dVoverV
print("Bulk Modulus : ",round(bulkmodulus,3)," lbf/ft^2 ")
print("Bulk Modulus : ",round(bulkmodulus/144,3)," psi ")
discussion
- Apply algebra, and find formula for the changing volume in terms of original volume.
- A harder way would be to compute initial mass from sp. weight, then compute needed volume change to make initial mass have supplied sp. weight; easier to do the algebra.
