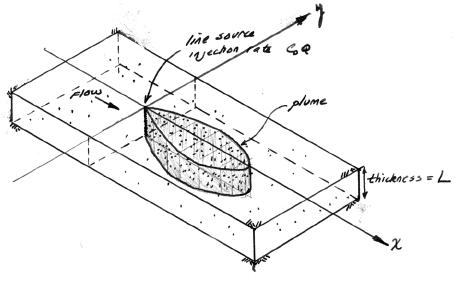
2D - Advection-Dispersion Constant Production (Injection) Source

The sketch depicts a vertical line source in an aquifer of infinite extent located at (x,y)=(0,0) some time after constant injection has begun. For the line source (injection well) whose fluid contribution makes negligible impact on the local hydraulics as depicted in the sketch the initial, boundary, and mass conservation conditions are:

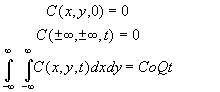
A solution is obtained by the time-convolution of an elementary line source solution is

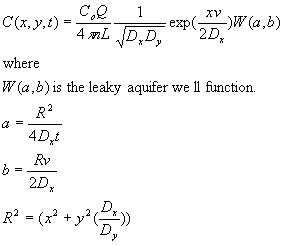
The leaky aquifer function can be evaluated numerically using the following recursive definition, or efficient approximations can be used. The solution herein uses polynomial and finite-series approximations.

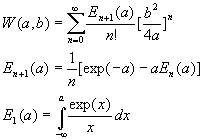
The solution is applicable for porous media flow, where the velocity (below) is the mean section velocity (seepage velocity divided by the porosity). The solution can also be used with streams and pipes (porosity = 1). Negative values of distance are not plotted in this interface, but the computed value at the point is correct.

References

Abramowitz, M. and I.A. Stegun, 1964. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. U.S. Department of Commerce, National Bureau of Standards, Applied Mathematics Series, Vol 55.

Walton, W.C., 1991. Principles of Groundwater Engineering, Lewin Publishers, Chelsea, Michigan.

Bear, J. 1972. Dynamics of Fluids in Porous Media. American Elsevier Publishing Company., Inc. New York, N.Y.

Interface

Enter Value for Distance along X-axis (x) :

Enter Value for Distance along Y-axis (y) :

Enter Value for Time (t) :

Enter Value for Longitudinal Dispersion Coefficient (Dx) :

Enter Value for Transverse Dispersion Coefficient (Dy) :

Enter Value for Mean Section Velocity (V) :

Enter Value for Injection Concentration (Co) :

Enter Value for Injection Rate (Q) :

Enter Value for Thickness (L)