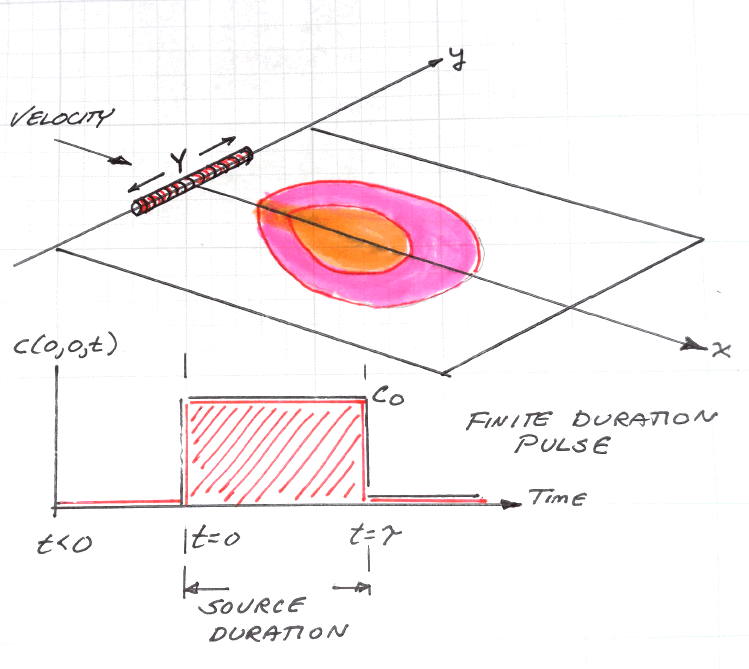
2D - Advection-Dispersion-Retardation-Decay, Finite-Width, Constant Source

The sketch depicts a finite-length horizontal line source in an aquifer of infinite extent located at (x,y)=(0,0). The lenght of the source zone (line) is Y. The source history is depicted beneath the sketch. The system starts with initial concentration of zero everywhere, at time t=0, the concentration in the source line increases to Co suddenly, and is maintained at that value for a specified duration (tau), when the source then decreases back to zero.

The transport processes modeled are advection along the x-axis, and dispersion in the x-direction (longitudinal) and in the y-direction (transverse).

The tracer decays using a first-order decay model.

The mathematical model is :

The analytical solution is approximated using CITE

Interface

Enter Value for Source Concentration (Co) in mg/L :

Enter Value for Distance along X-axis (x) in meters :

Enter Value for Distance along Y-axis (y) in meters :

Enter Value for Longitudinal Dispersion Coefficient (Dx) in meters^2/day :

Enter Value for Transverse Dispersion Coefficient (Dy) in meters^2/day:

Enter Value for Mean Section Velocity (V) in meters/day :

Enter Value for Time (t) in days :

Enter Value for Source Duration (tau) in days :

Enter Source Width (Y) in meters :

Enter Value for 1-st Order Decay Rate (lambda) in 1/days

References

Abramowitz, M. and I.A. Stegun, 1964. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. U.S. Department of Commerce, National Bureau of Standards, Applied Mathematics Series, Vol 55.

Walton, W.C., 1991. Principles of Groundwater Engineering, Lewin Publishers, Chelsea, Michigan.

Bear, J. 1972. Dynamics of Fluids in Porous Media. American Elsevier Publishing Company., Inc. New York, N.Y.