%%html
<!--Script block to left align Markdown Tables-->
<style>
table {margin-left: 0 !important;}
</style>
# Preamble script block to identify host, user, and kernel
import sys
! hostname
! whoami
print(sys.executable)
print(sys.version)
print(sys.version_info)
Data Modeling: Regression Approach¶
Regression is a basic and commonly used type of predictive analysis.
The overall idea of regression is to assess:
- does a set of predictor/explainatory variables (features) do a good job in predicting an outcome (dependent/response) variable?
- Which explainatory variables (features) in particular are significant predictors of the outcome variable, and in what way do they–indicated by the magnitude and sign of the beta estimates–impact the outcome variable?
- What is the estimated(predicted) value of the response under various excitation (explainatory) variable values?
- What is the uncertainty involved in the prediction?
These regression estimates are used to explain the relationship between one dependent variable and one or more independent variables.
The simplest form is a linear regression equation with one dependent(response) and one independent(explainatory) variable is defined by the formula
$y_i = \beta_0 + \beta_1*x_i$, where $y_i$ = estimated dependent(response) variable value, $\beta_0$ = constant(intercept), $\beta_1$ = regression coefficient (slope), and $x_i$ = independent(predictor) variable value
Outline¶
- Linear Regression – purpose
- Background and simple by-hand examples
- Linear systems representation(s)
Objectives¶
- Create linear regression models from data using primitive python
- Create linear regression models from data using NumPy and Pandas tools
- Create presentation-quality graphs and charts for reporting results
Computational Thinking¶
| Description | Computational Thinking Concept |
|---|---|
| Linear Model | Abstraction |
| Response and Explanatory Variables | Decomposition |
| Primitive arrays: vectors and matrices | Data Representation |
| NumPy arrays: vectors and matrices | Data Representation |
Fundamental Questions¶
- What is regression used for?
- Why is it useful?
Three major uses for regression analysis are (1) determining the strength of predictors, (2) forecasting an effect, and (3) trend forecasting.
First, the regression might be used to identify the strength of the effect that the independent variable(s) have on a dependent variable. Typical questions are what is the strength of relationship between dose and effect, sales and marketing spending, or age and income.
Second, it can be used to forecast effects or impact of changes. That is, the regression analysis helps us to understand how much the dependent variable changes with a change in one or more independent variables. A typical question is, “how much additional sales income do I get for each additional $1000 spent on marketing?”
Third, regression analysis predicts trends and future values. The regression analysis can be used to get point estimates. A typical question is, “what will the price of gold be in 6 months?”
Consider the image below from a Texas Instruments Calculator user manual
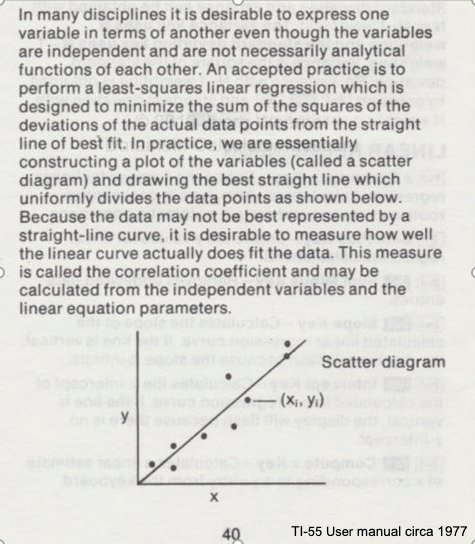
In the context of our class, the straight solid line is the Data Model whose equation is
$Y = \beta_0 + \beta_1*X$.
The ordered pairs $(x_i,y_i)$ in the scatterplot are the observation (or training set).
As depicted here $Y$ is the response to different values of the explainitory variable $X$. The typical convention is response on the up-down axis, but not always.
The model parameters are $\beta_0$ and $\beta_1$ ; once known can estimate (predict) response to (as yet) unobserved values of $x$
Classically, the normal equations are evaluated to find the model parameters:
$\beta_1 = \frac{\sum x\sum y~-~N\sum xy}{(\sum x)^2~-~N\sum x^2}$ and $\beta_0 = \bar y - \beta_1 \bar x$
Classical Regression by Normal Equations¶
We will illustrate the classical approach to finding the slope and intercept using the normal equations first a plotting function, then we will use the values from the Texas Instruments TI-55 user manual.
### Lets Make a Plotting Package
def makeAbear(xvalues,yvalues,xleft,yleft,xright,yright,xlab,ylab,title):
# plotting function dependent on matplotlib installed above
# xvalues, yvalues == data pairs to scatterplot; FLOAT
# xleft,yleft == left endpoint line to draw; FLOAT
# xright,yright == right endpoint line to draw; FLOAT
# xlab,ylab == axis labels, STRINGS!!
# title == Plot title, STRING
import matplotlib.pyplot
matplotlib.pyplot.scatter(xvalues,yvalues)
matplotlib.pyplot.plot([xleft, xright], [yleft, yright], 'k--', lw=2, color="red")
matplotlib.pyplot.xlabel(xlab)
matplotlib.pyplot.ylabel(ylab)
matplotlib.pyplot.title(title)
matplotlib.pyplot.show()
return
# Make two lists
sample_length = [101.3,103.7,98.6,99.9,97.2,100.1]
sample_weight = [609,626,586,594,579,605]
# We will assume weight is the explainatory variable, and it is to be used to predict length.
makeAbear(sample_weight, sample_length,580,96,630,106,'Weight (g)','Length (cm)','Length versus Weight for \n NASA CF0132 Fiber Reinforced Polymer')
Notice the dashed line, we supplied only two (x,y) pairs to plot the line, so lets get a colonoscope and find where it came from.
def myline(slope,intercept,value1,value2):
'''Returns a tuple ([x1,x2],[y1,y2]) from y=slope*value+intercept'''
listy = []
listx = []
listx.append(value1)
listx.append(value2)
listy.append(slope*listx[0]+intercept)
listy.append(slope*listx[1]+intercept)
return(listx,listy)
slope = 0.129 #0.13
intercept = 22.813 # 23
xlow = 580
xhigh = 630
object = myline(slope,intercept,xlow,xhigh)
xone = object[0][0]; xtwo = object[0][1]; yone = object[1][0]; ytwo = object[1][1]
makeAbear(sample_weight, sample_length,xone,yone,xtwo,ytwo,'Weight (g)','Length (cm)','Length versus Weight for \n NASA CF0132 Fiber Reinforced Polymer')
print(xone,yone)
print(xtwo,ytwo)
# Evaluate the normal equations
sumx = 0.0
sumy = 0.0
sumxy = 0.0
sumx2 = 0.0
sumy2 = 0.0
for i in range(len(sample_weight)):
sumx = sumx + sample_weight[i]
sumx2 = sumx2 + sample_weight[i]**2
sumy = sumy + sample_length[i]
sumy2 = sumy2 + sample_length[i]**2
sumxy = sumxy + sample_weight[i]*sample_length[i]
b1 = (sumx*sumy - len(sample_weight)*sumxy)/(sumx**2-len(sample_weight)*sumx2)
b0 = sumy/len(sample_length) - b1* (sumx/len(sample_weight))
lineout = ("Linear Model is y=%.3f" % b1) + ("x + %.3f" % b0)
print("Linear Model is y=%.3f" % b1 ,"x + %.3f" % b0)
slope = 0.129 #0.129
intercept = 22.813 # 22.813
xlow = 580
xhigh = 630
object = myline(slope,intercept,xlow,xhigh)
xone = object[0][0]; xtwo = object[0][1]; yone = object[1][0]; ytwo = object[1][1]
makeAbear(sample_weight, sample_length,xone,yone,xtwo,ytwo,'Weight (g)','Length (cm)','Length versus Weight for \n NASA CF0132 Fiber Reinforced Polymer')
Where do these normal equations come from?¶
Consider our linear model $y = \beta_0 + \beta_1 \cdot x + \epsilon$. Where $\epsilon$ is the error in the estimate. If we square each error and add them up (for our training set) we will have $\sum \epsilon^2 = \sum (y_i - \beta_0 - \beta_1 \cdot x_i)^2 $. Our goal is to minimize this error by our choice of $\beta_0 $ and $ \beta_1 $
The necessary and sufficient conditions for a minimum is that the first partial derivatives of the error as a function must vanish (be equal to zero). We can leverage that requirement as
$\frac{\partial(\sum \epsilon^2)}{\partial \beta_0} = \frac{\partial{\sum (y_i - \beta_0 - \beta_1 \cdot x_i)^2}}{\partial \beta_0} = - \sum 2[y_i - \beta_0 + \beta_1 \cdot x_i] = -2(\sum_{i=1}^n y_i - n \beta_0 - \beta_1 \sum_{i=1}^n x_i) = 0 $
and
$\frac{\partial(\sum \epsilon^2)}{\partial \beta_1} = \frac{\partial{\sum (y_i - \beta_0 - \beta_1 \cdot x_i)^2}}{\partial \beta_1} = - \sum 2[y_i - \beta_0 + \beta_1 \cdot x_i]x_i = -2(\sum_{i=1}^n x_i y_i - n \beta_0 \sum_{i=1}^n x_i - \beta_1 \sum_{i=1}^n x_i^2) = 0 $
Solving the two equations for $\beta_0$ and $\beta_1$ produces the normal equations (for linear least squares), which leads to
$\beta_1 = \frac{\sum x\sum y~-~n\sum xy}{(\sum x)^2~-~n\sum x^2}$ $\beta_0 = \bar y - \beta_1 \bar x$
Lets consider a more flexible way by fitting the data model using linear algebra instead of the summation notation.
Computational Linear Algebra¶
We will start again with our linear data model
$y_i = \beta_0 + \beta_1 \cdot x_i + \epsilon_i$ then replace with vectors as
\begin{gather} \mathbf{Y}= \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \\ \end{pmatrix} \end{gather}\begin{gather} \mathbf{\beta}= \begin{pmatrix} \beta_0 \\ \beta_1 \\ \end{pmatrix} \end{gather}\begin{gather} \mathbf{X}= \begin{pmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots \\ 1 & x_n \\ \end{pmatrix} \end{gather}\begin{gather} \mathbf{\epsilon}= \begin{pmatrix} \epsilon_1 \\ \epsilon_2 \\ \vdots \\ \epsilon_n \\ \end{pmatrix} \end{gather}So our system can now be expressed in matrix-vector form as
$\mathbf{Y}=\mathbf{X}\mathbf{\beta}+\mathbf{\epsilon}$ if we perfrom the same vector calculus as before we will end up with a result where pre-multiply by the transpose of $\mathbf{X}$ we will have a linear system in $\mathbf{\beta}$ which we can solve using Gaussian reduction, or LU decomposition or some other similar method.
The resulting system (that minimizes $\mathbf{\epsilon^T}\mathbf{\epsilon}$) is
$\mathbf{X^T}\mathbf{Y}=\mathbf{X^T}\mathbf{X}\mathbf{\beta}$ and solving for the parameters gives $\mathbf{\beta}=(\mathbf{X^T}\mathbf{X})^{-1}\mathbf{X^T}\mathbf{Y}$
So lets apply it to our example - what follows is mostly in python primative
# linearsolver with pivoting adapted from
# https://stackoverflow.com/questions/31957096/gaussian-elimination-with-pivoting-in-python/31959226
def linearsolver(A,b):
n = len(A)
M = A
i = 0
for x in M:
x.append(b[i])
i += 1
# row reduction with pivots
for k in range(n):
for i in range(k,n):
if abs(M[i][k]) > abs(M[k][k]):
M[k], M[i] = M[i],M[k]
else:
pass
for j in range(k+1,n):
q = float(M[j][k]) / M[k][k]
for m in range(k, n+1):
M[j][m] -= q * M[k][m]
# allocate space for result
x = [0 for i in range(n)]
# back-substitution
x[n-1] =float(M[n-1][n])/M[n-1][n-1]
for i in range (n-1,-1,-1):
z = 0
for j in range(i+1,n):
z = z + float(M[i][j])*x[j]
x[i] = float(M[i][n] - z)/M[i][i]
# return result
return(x)
#######
# matrix multiply script
def mmult(amatrix,bmatrix,rowNumA,colNumA,rowNumB,colNumB):
result_matrix = [[0 for j in range(colNumB)] for i in range(rowNumA)]
for i in range(0,rowNumA):
for j in range(0,colNumB):
for k in range(0,colNumA):
result_matrix[i][j]=result_matrix[i][j]+amatrix[i][k]*bmatrix[k][j]
return(result_matrix)
# matrix vector multiply script
def mvmult(amatrix,bvector,rowNumA,colNumA):
result_v = [0 for i in range(rowNumA)]
for i in range(0,rowNumA):
for j in range(0,colNumA):
result_v[i]=result_v[i]+amatrix[i][j]*bvector[j]
return(result_v)
colNumX=2 #
rowNumX=len(sample_weight)
xmatrix = [[1 for j in range(colNumX)]for i in range(rowNumX)]
xtransp = [[1 for j in range(rowNumX)]for i in range(colNumX)]
yvector = [0 for i in range(rowNumX)]
for irow in range(rowNumX):
xmatrix[irow][1]=sample_weight[irow]
xtransp[1][irow]=sample_weight[irow]
yvector[irow] =sample_length[irow]
xtx = [[0 for j in range(colNumX)]for i in range(colNumX)]
xty = []
xtx = mmult(xtransp,xmatrix,colNumX,rowNumX,rowNumX,colNumX)
xty = mvmult(xtransp,yvector,colNumX,rowNumX)
beta = []
#solve XtXB = XtY for B
beta = linearsolver(xtx,xty) #Solve the linear system
slope = beta[1] #0.129
intercept = beta[0] # 22.813
xlow = 580
xhigh = 630
object = myline(slope,intercept,xlow,xhigh)
xone = object[0][0]; xtwo = object[0][1]; yone = object[1][0]; ytwo = object[1][1]
makeAbear(sample_weight, sample_length,xone,yone,xtwo,ytwo,'Weight (g)','Length (cm)','Length versus Weight for \n NASA CF0132 Fiber Reinforced Polymer')
beta
What's the Value of the Computational Linear Algebra ?¶
The value comes when we have more explainatory variables, and we may want to deal with curvature.
# Make two lists
yyy = [0,0,1,1,3]
xxx = [-2,-1,0,1,2]
slope = 0.5 #0.129
intercept = 1 # 22.813
xlow = -3
xhigh = 3
object = myline(slope,intercept,xlow,xhigh)
xone = object[0][0]; xtwo = object[0][1]; yone = object[1][0]; ytwo = object[1][1]
makeAbear(xxx, yyy,xone,yone,xtwo,ytwo,'xxx','yyy','yyy versus xxx')
colNumX=2 #
rowNumX=len(xxx)
xmatrix = [[1 for j in range(colNumX)]for i in range(rowNumX)]
xtransp = [[1 for j in range(rowNumX)]for i in range(colNumX)]
yvector = [0 for i in range(rowNumX)]
for irow in range(rowNumX):
xmatrix[irow][1]=xxx[irow]
xtransp[1][irow]=xxx[irow]
yvector[irow] =yyy[irow]
xtx = [[0 for j in range(colNumX)]for i in range(colNumX)]
xty = []
xtx = mmult(xtransp,xmatrix,colNumX,rowNumX,rowNumX,colNumX)
xty = mvmult(xtransp,yvector,colNumX,rowNumX)
beta = []
#solve XtXB = XtY for B
beta = linearsolver(xtx,xty) #Solve the linear system
slope = beta[1] #0.129
intercept = beta[0] # 22.813
xlow = -3
xhigh = 3
object = myline(slope,intercept,xlow,xhigh)
xone = object[0][0]; xtwo = object[0][1]; yone = object[1][0]; ytwo = object[1][1]
makeAbear(xxx, yyy,xone,yone,xtwo,ytwo,'xxx','yyy','yyy versus xxx')
colNumX=3 #
rowNumX=len(xxx)
xmatrix = [[1 for j in range(colNumX)]for i in range(rowNumX)]
xtransp = [[1 for j in range(rowNumX)]for i in range(colNumX)]
yvector = [0 for i in range(rowNumX)]
for irow in range(rowNumX):
xmatrix[irow][1]=xxx[irow]
xmatrix[irow][2]=xxx[irow]**2
xtransp[1][irow]=xxx[irow]
xtransp[2][irow]=xxx[irow]**2
yvector[irow] =yyy[irow]
xtx = [[0 for j in range(colNumX)]for i in range(colNumX)]
xty = []
xtx = mmult(xtransp,xmatrix,colNumX,rowNumX,rowNumX,colNumX)
xty = mvmult(xtransp,yvector,colNumX,rowNumX)
beta = []
#solve XtXB = XtY for B
beta = linearsolver(xtx,xty) #Solve the linear system
howMany = 20
xlow = -2
xhigh = 2
deltax = (xhigh - xlow)/howMany
xmodel = []
ymodel = []
for i in range(howMany+1):
xnow = xlow + deltax*float(i)
xmodel.append(xnow)
ymodel.append(beta[0]+beta[1]*xnow+beta[2]*xnow**2)
# Now plot the sample values and plotting position
import matplotlib.pyplot
myfigure = matplotlib.pyplot.figure(figsize = (10,5)) # generate a object from the figure class, set aspect ratio
# Built the plot
matplotlib.pyplot.scatter(xxx, yyy, color ='blue')
matplotlib.pyplot.plot(xmodel, ymodel, color ='red')
matplotlib.pyplot.ylabel("Y")
matplotlib.pyplot.xlabel("X")
mytitle = "YYY versus XXX"
matplotlib.pyplot.title(mytitle)
matplotlib.pyplot.show()
### Now using numpy