Download this page as a jupyter notebook at Lesson 9

ENGR 1330 Computational Thinking with Data Science

Copyright © 2021 Theodore G. Cleveland and Farhang Forghanparast

Last GitHub Commit Date: 10 September 2021

Lesson 9 Matrix Arithmetic using NumPy:

Objectives

Numpy

Numpy is the core library for scientific computing in Python. It provides a high-performance multidimensional array object, and tools for working with these arrays. The library’s name is short for “Numeric Python” or “Numerical Python”. If you are curious about NumPy, this cheat sheet is recommended: https://s3.amazonaws.com/assets.datacamp.com/blog_assets/Numpy_Python_Cheat_Sheet.pdf

NumPy library has two fundamental conceptualizations:

Computational Thinking Concepts

The CT concepts expressed within NumPy include:

Module Set-Up

In principle, NumPy should be available in a default Anaconda install

How to check

If you do get an error, that means that you will have to install using conda or pip; you are on-your-own here! On the content server the process is:

  1. Open a new terminal from the launcher
  2. Change to root user su then enter the root password
  3. sudo -H /opt/jupyterhib/bin/python3 -m pip install numpy
  4. Wait until the install is complete; for security, user compthink is not in the sudo group
  5. Verify the install by trying to execute import numpy as above.

The process will be similar on a Macintosh, or Windows. Best is to hope you have a sucessful anaconda install.

If you have to do this kind of install, you will have to do some reading, some references I find useful are:

  1. https://jupyterlab.readthedocs.io/en/stable/user/extensions.html
  2. https://www.pugetsystems.com/labs/hpc/Note-How-To-Install-JupyterHub-on-a-Local-Server-1673/#InstallJupyterHub
  3. https://jupyterhub.readthedocs.io/en/stable/installation-guide-hard.html (This is the approach on the content server which has a functioning JupyterHub)

NumPy: AKA Numerical Python

NumPy is a foundational library (module) for scientific computing. Most if not all all data science libraries (modules) rely on NumPy as one of their building blocks to reduce the need to build certain operations in primative python.

NumPy provides a multi-dimensional array object called ‘ndarray’ (n-dimensional array) and methods for:

As compared to the prior lesson, multi-dimensional arrays (lists) are far easier to manipulate using numpy.

Arrays

A numpy array is a grid of values, all of the same type, and is indexed by a tuple of nonnegative integers. The number of dimensions is the rank of the array; the shape of an array is a tuple of integers giving the size of the array along each dimension.

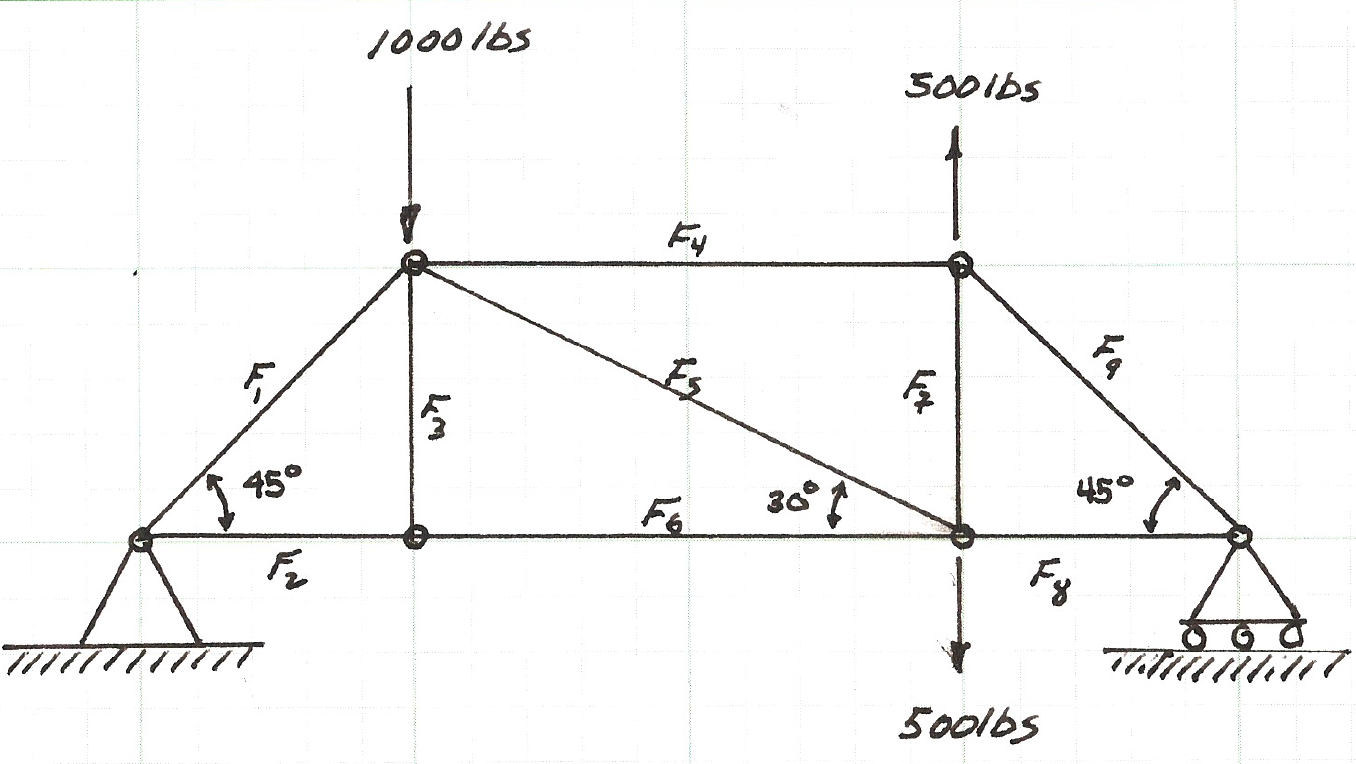
Figure 1 is a visual depiction of numpy arrays of rank 1 and rank2.

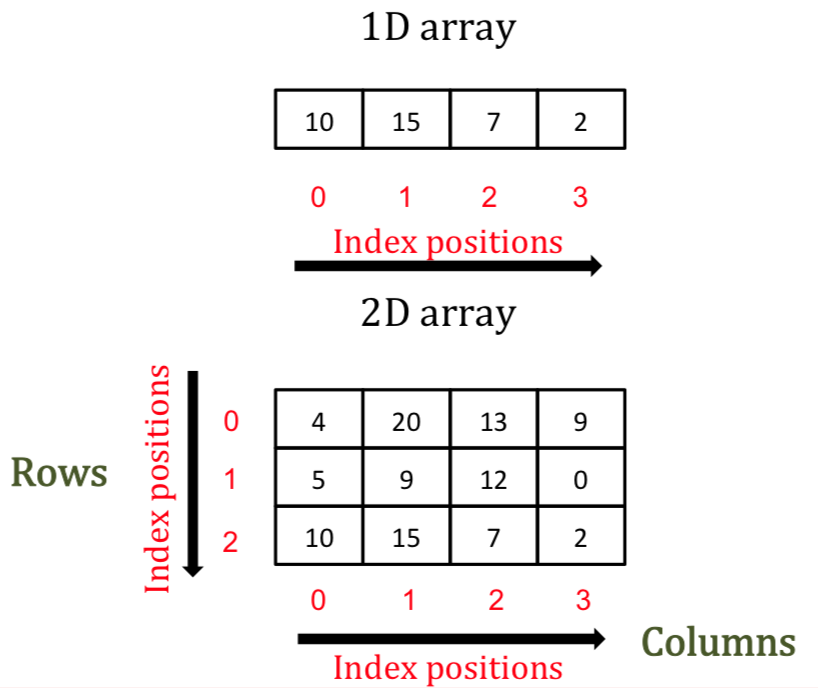
Figure 1: NumPy array visual representation

In other words, an array contains information about the raw data, how to locate an element and how to interpret an element.To make a numpy array, you can just use the np.array() function. All you need to do is pass a list to it. Don’t forget that, in order to work with the np.array() function, you need to make sure that the numpy library is present in your environment. If you want to read more about the differences between a Python list and NumPy array, this link is recommended: https://webcourses.ucf.edu/courses/1249560/pages/python-lists-vs-numpy-arrays-what-is-the-difference

Example- 1D Arrays (Vectors)

Let's create a 1D array from the 2000s (2000-2009):

Example: n-Dimensional Arrays

We already made a 3X3 array, but let's create a 5x2 array from the 2000s (2000-2009):

Array Arithmetic

Once you have created the arrays, you can do basic Numpy operations. Numpy offers a variety of operations applicable on arrays. From basic operations such as summation, subtraction, multiplication and division to more advanced and essential operations such as matrix multiplication and other elementwise operations. In the examples below, we will go over some of these:

Example- 1D Array Arithmetic

Lets do scalar multiplication, first as just a list!

Now using numpy

Example- n-Dimensional Array Arithmetic

Recall how we have to do the same if using ordinary lists, just for the first line in the block above:

There is considerable savings in code crafting using numpy; hence its popularity and utility.

Other functions to create NumPy arrays easily

Functions to do basic operations on NumPy arrays

Functions to do mathematical operations on NumPy arrays

Indexing: An important step in manipulating and analyzing arrays

There are linear algebra functions too, recall our matrices

\begin{gather} \mathbf{A}= \begin{pmatrix} 2 & 3 \\ 4 & -3 \\ \end{pmatrix} \end{gather}\begin{gather} \mathbf{A}^{-1}= \begin{pmatrix} \frac{1}{6} & \frac{1}{6} \\ ~\\ \frac{2}{9} & -\frac{1}{9} \\ \end{pmatrix} \end{gather}

We can get the inverse in numpy from:

Arrays Comparison

Comparing two NumPy arrays determines whether they are equivalent by checking if every element at each corresponding index are the same.

Example- 1D Array Comparison

Example n-Dimensional Array Comparison

Using the numbers below:

4,9,23,39,40,55,68,72

A) Create a 2x2 array with all the even numbers and print it out
B) Create a 2x2 array with all the odd numbers and print it out

C) Compare the two arrays using the "less_equal" function from numpy package

Arrays Manipulation

numpy.copy() allows us to create a copy of an array. This method is particularly useful when we need to manipulate an array while keeping an original copy in memory.

The numpy.delete() function returns a new array with sub-arrays along an axis deleted. Let's have a look at the examples.

Examples: Copying and Deleting Arrays and Elements

Below we will work a few examples.

now lets change a value in x, then print the contents again

Notice how x and y reflect the change, whats going on? The assignment statement y = x creates equivalence in numpy; that is x and y are different names for the same object. We can verify using the id() function which will return the address in memory of the head of the object.

Sorting Arrays

Sorting means putting elements in an ordered sequence. Ordered sequence is any sequence that has an order corresponding to elements, like numeric or alphabetical, ascending or descending. If you use the sort() method on a 2-D array, both arrays will be sorted.

Example: Sorting 1D Arrays

Define a 1D array as ['FIFA 2020','Red Dead Redemption','Fallout','GTA','NBA 2018','Need For Speed'] and print it out. Then, sort the array alphabetically._

Example- Sorting n-Dimensional Arrays

Define a 3x3 array with 17,-6,2,86,-12,0,0,23,12 and print it out. Then, sort the array.

Partitioning (Slice) Arrays

Slicing in python means taking elements from one given index to another given index.

Example- Slicing 1D Arrays

Define a 1D array as [1,3,5,7,9], slice out the [3,5,7] and print it out.

Example- Slicing n-Dimensional Arrays

Define a 5x5 array with "Superman, Batman, Jim Hammond, Captain America, Green Arrow, Aquaman, Wonder Woman, Martian Manhunter, Barry Allen, Hal Jordan, Hawkman, Ray Palmer, Spider Man, Thor, Hank Pym, Solar, Iron Man, Dr. Strange, Daredevil, Ted Kord, Captian Marvel, Black Panther, Wolverine, Booster Gold, Spawn " and print it out. Then:

Illustration of NumPy on a mechanics problem

Problem Statement

The figure below is a simply supported, statically determinate truss with pin connections (zero moment transfer connections). Find the forces in each member for the loading shown.

This notebook will illustrate how to leverage a linear systems solver(s) to analyze the truss. The approach uses concepts from statics and computational thinking.

From statics

From computational thinking

Before even contemplating writing/using a program we need to build a mathematical model of the truss and assemble the system of linear equations that result from the model.

So the first step is to sketch a free-body-diagram as below and build a node naming convention and force names.

Next we will write the force balance for each of the six nodes ($N1$-$N6$), which will produce a total of 12 equations in the 12 unknowns (the 9 member forces, and 3 reactions).

The figure below is the force balance for node $N1$, the two force equations (for the horizontal, $x$, direction and the vertical, $y$, direction) are listed below the figure.

$$\begin{gather} \begin{matrix} \sum F_x = 0 = & +F_1cos(45) & + F_2 & & & & & & & + A_x & & & & & \\ \sum F_y = 0 = & +F_1sin(45) & & & & & & & & & & + A_y & & & \\ \end{matrix} \end{gather}$$

The equation above is the force balance equation pair for the node. The $x$ component equation will later be named $N1_x$ to indicate it arises from Node 1, $x$ component equation. A similar notation convention will also be adopted for the $y$ component equation. There will be an equation pair for each node.

Below is a sketch of the force balance for node $N2$, the two force equations (for the horizontal, $x$, direction and the vertical, $y$, direction) are listed below the figure.

\begin{gather} \begin{matrix} \sum F_x = 0 = & & -F_2 & & & & +F_6 & & & & & & & & \\ \sum F_y = 0 = & & & +F_3 & & & & & & & & & & & \\ \end{matrix} \end{gather}

Below is a sketch of the force balance for node $N3$, the two force equations (for the horizontal, $x$, direction and the vertical, $y$, direction) are listed below the figure.

\begin{gather} \begin{matrix} \sum F_x = 0 = & & & & & -F_5cos(30) & -F_6 & & +F_8 & & & & & & \\ \sum F_y = 0 = & & & & & F_5sin(30) & & +F_7 & & & & & & & -P_3\\ \end{matrix} \end{gather}

Above is the force balance equation pair for node $N3$.

Below is a sketch of the force balance for node $N4$, the two force equations (for the horizontal, $x$, direction and the vertical, $y$, direction) are listed below the figure.

\begin{gather} \begin{matrix} \sum F_x = 0 = & & & & & & & & -F_8 & -F_9cos(45) & & & & & \\ \sum F_y = 0 = & & & & & & & & & F_9sin(45) & & & +B_y & & \\ \end{matrix} \end{gather}

Above is the force balance equation pair for node $N4$.

Below is a sketch of the force balance for node $N5$, the two force equations (for the horizontal, $x$, direction and the vertical, $y$, direction) are listed below the figure.

\begin{gather} \begin{matrix} \sum F_x = 0 = & -F_1cos(45) & & & +F_4 & +F_5cos(30) & & & & & & & & & \\ \sum F_y = 0 = & -F_1sin(45) & & -F_3 & & -F_5sin(30) & & & & & & & & & -P_1\\ \end{matrix} \end{gather}

Above is the force balance equation pair for node $N5$.

Below is a sketch of the force balance for node $N6$, the two force equations (for the horizontal, $x$, direction and the vertical, $y$, direction) are listed below the figure.

\begin{gather} \begin{matrix} \sum F_x = 0 = & & & & -F_4 & & & & & F_9sin(45) & & & & & \\ \sum F_y = 0 = & & & & & & & -F_7 & & -F_9cos(45) & & & & & P_2\\ \end{matrix} \end{gather}

Above is the force balance equation pair for node $N6$.

The next step is to gather the equation pairs into a system of linear equations.
We will move the known loads to the right hand side and essentially construct the matrix equation $\mathbf{A}\mathbf{x} = \mathbf{b}$.

The system below is a matrix representation of the equation pairs with the forces moved to the right hand side $\mathbf{b} = RHS$.

\begin{gather} \begin{pmatrix} ~ & F_1 & F_2 & F_3 & F_4 & F_5 & F_6 & F_7 & F_8 & F_9 & A_x & A_y & B_y & | & RHS\\ \hline N1_x & 0.707 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & | & 0\\ N1_y & 0.707 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & | & 0\\ N2_x & 0 & -1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & | & 0\\ N2_y & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | & 0\\ N3_x & 0 & 0 & 0 & 0 & -0.866 & -1 & 0 & 1 & 0 & 0 & 0 & 0 & | & 0\\ N3_y & 0 & 0 & 0 & 0 & 0.5 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & | & P_3\\ N4_x & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & -0.707 & 0 & 0 & 0 & | & 0\\ N4_y & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0.707 & 0 & 0 & 0 & | & 0\\ N5_x & -0.707 & 0 & 0 & 1 & 0.866 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | & 0\\ N5_y & -0.707 & 0 & -1 & 0 & -0.5 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & | & P_1\\ N6_x & 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0.707 & 0 & 0 & 0 & | & 0\\ N6_y & 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & -0.707 & 0 & 0 & 0 & | & -P_2\\ \end{pmatrix} \end{gather}

In the system, the rows are labeled on the left-most column with their node-related equation name.
Thus each row of the matrix corresponds to an equation derived from a node.
The columns are labeled with their respective unknown force (except the last column, which represents the right-hand-side of the system of linear equations).
Thus the coefficient in each column corresponds to a force in each node equation.
The sign of the coefficient refers to the assumed direction the force acts.

In the analysis all the members were assumed to be in tension (except for the reaction forces).
If a coefficient has a value of zero in a particular row, then that force does no act at the node to which the row corresponds.

From this representation the transition to the formal vector-matrix representation is straightforward.

\begin{gather} \mathbf{A} = \begin{pmatrix} 0.707 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0.707 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & -1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -0.866 & -1 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0.5 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & -0.707 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0.707 & 0 & 0 & 0 \\ -0.707 & 0 & 0 & 1 & 0.866 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ -0.707 & 0 & -1 & 0 & -0.5 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -1 & 0 & 0 & 0 & 0 & 0.707 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & -1 & 0 & -0.707 & 0 & 0 & 0 \\ \end{pmatrix} \end{gather}\begin{gather} \mathbf{x} = \begin{pmatrix} F_1\\ F_2\\ F_3\\ F_4\\ F_5\\ F_6\\ F_7\\ F_8\\ F_9\\ A_x\\ A_y\\ B_y\\ \end{pmatrix} \end{gather}\begin{gather} \mathbf{b} = \begin{pmatrix} 0\\ 0\\ 0\\ 0\\ 0\\ P_3\\ 0\\ 0\\ 0\\ P_1\\ 0\\ -P_2\\ \end{pmatrix} \end{gather}

The various matrices above are entere into text files named A.txt and B.txt

Now we use our solver tools, here I have not done much on tidy output, thats left for the reader.

Now lets do the same tasks using numpy

References

Johnson, J. (2020). Python Numpy Tutorial (with Jupyter and Colab). Retrieved September 15, 2020, from https://cs231n.github.io/python-numpy-tutorial/

Willems, K. (2019). (Tutorial) Python NUMPY Array TUTORIAL. Retrieved September 15, 2020, from https://www.datacamp.com/community/tutorials/python-numpy-tutorial?utm_source=adwords_ppc

Willems, K. (2017). NumPy Cheat Sheet: Data Analysis in Python. Retrieved September 15, 2020, from https://www.datacamp.com/community/blog/python-numpy-cheat-sheet

W3resource. (2020). NumPy: Compare two given arrays. Retrieved September 15, 2020, from https://www.w3resource.com/python-exercises/numpy/python-numpy-exercise-28.php

Sorting https://www.programiz.com/python-programming/methods/list/sort

Overland, B. (2018). Python Without Fear. Addison-Wesley ISBN 978-0-13-468747-6.

Grus, Joel (2015). Data Science from Scratch: First Principles with Python O’Reilly Media. Kindle Edition.

Precord, C. (2010) wxPython 2.8 Application Development Cookbook Packt Publishing Ltd. Birmingham , B27 6PA, UK ISBN 978-1-849511-78-0.