%%html
<!--Script block to left align Markdown Tables-->
<style>
table {margin-left: 0 !important;}
</style>
# Preamble script block to identify host, user, and kernel
import sys
! hostname
! whoami
print(sys.executable)
print(sys.version)
print(sys.version_info)
Laboratory 5. Functions¶
Functions are simply pre-written code fragments that perform a certain task. In older procedural languages functions and subroutines are similar, but a function returns a value whereas a subroutine operates on data. The difference is subtle but important.
More recent thinking has functions being able to operate on data (they always could) and the value returned may be simply an exit code.
An analogy are the functions in MS Excel.
To add numbers, we can use the sum(range) function and type =sum(A1:A5) instead of typing =A1+A2+A3+A4+A5
Calling the Function¶
We call a function simply by typing the name of the function or by using the dot notation. Whether we can use the dot notation or not depends on how the function is written, whether it is part of a class, and how it is imported into a program.
Some functions expect us to pass data to them to perform their tasks. These dataare known as parameters( older terminology is arguments, or argument list) and we pass them to the function by enclosing their values in parenthesis ( ) separated by commas.
For instance, the print() function for displaying text on the screen is \called" by typing print('Hello World') where print is the name of the function and the literal (a string) 'Hello World' is the argument.
Program flow¶
A function, whether built-in, or added must be defined before it is called, otherwise the script will fail. Certain built-in functions "self define" upon start (such as print() and type() and we need not worry about those funtions). The diagram below illustrates the requesite flow control for functions that need to be defined before use.
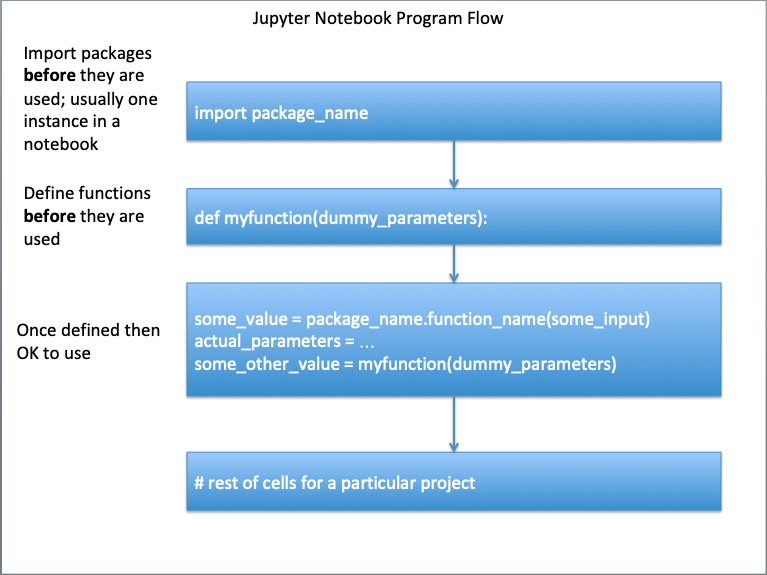
An example below will illustrate, change the cell to code and run it, you should get an error. Then fixt the indicated line (remove the leading "#" in the import math ... line) and rerun, should get a functioning script.
# reset the notebook using a magic function in JupyterLab
%reset -f
# An example, run once as is then activate indicated line, run again - what happens?
x= 4.
sqrt_by_arithmetic = x**0.5
print('Using arithmetic square root of ', x, ' is ',sqrt_by_arithmetic )
#import math # import the math package ## activate and rerun
sqrt_by_math = math.sqrt(x) # note the dot notation
print('Using math package square root of ', x,' is ',sqrt_by_arithmetic)
An alternate way to load just the sqrt() function is shown below, either way is fine.
# reset the notebook using a magic function in JupyterLab
%reset -f
# An example, run once as is then activate indicated line, run again - what happens?
x= 4.
sqrt_by_arithmetic = x**0.5
print('Using arithmetic square root of ', x, ' is ',sqrt_by_arithmetic )
#from math import sqrt # import sqrt from the math package ## activate and rerun
sqrt_by_math = sqrt(x) # note the notation
print('Using math package square root of ', x,' is ',sqrt_by_arithmetic)
Built-In in Primitive Python (Base install)¶
The base Python functions and types built into it that are always available, the figure below lists those functions.
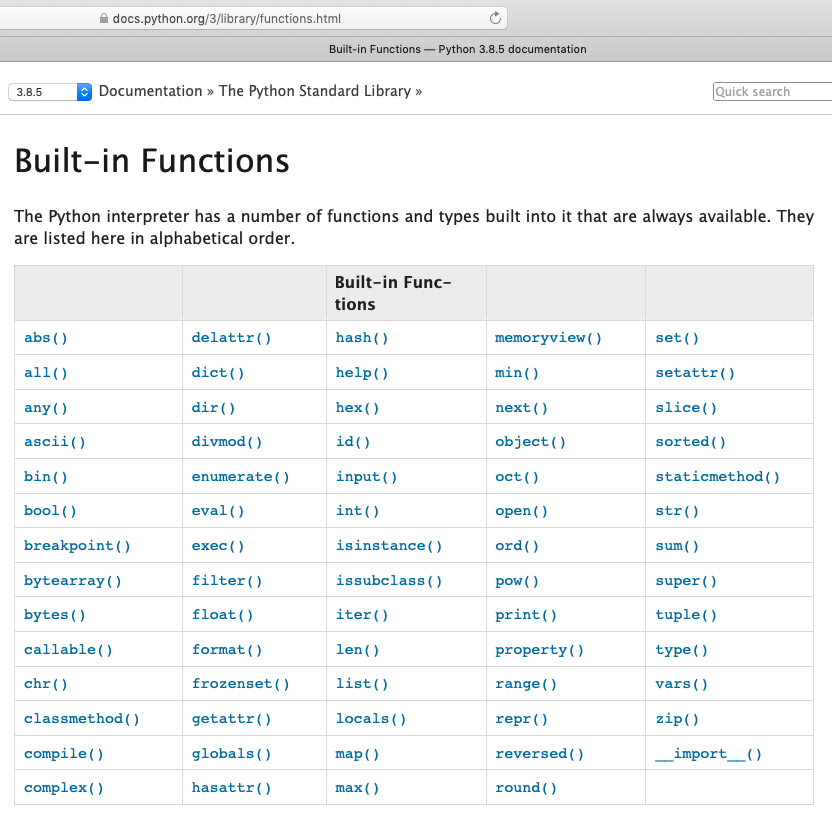
Notice all have the structure of function_name(), except __import__() which has a constructor type structure, and is not intended for routine use. We will learn about constructors later.
Added-In using External Packages/Modules and Libaries (e.g. math)¶
Python is also distributed with a large number of external functions. These functions are saved in files known as modules. To use the built-in codes in Python modules, we have to import them into our programs first. We do that by using the import keyword. There are three ways to import:
- Import the entire module by writing import moduleName; For instance, to import the random module, we write import random. To use the randrange() function in the random module, we write random.randrange( 1, 10);28
- Import and rename the module by writing import random as r (where r is any name of your choice). Now to use the randrange() function, you simply write r.randrange(1, 10); and
- Import speci c functions from the module by writing from moduleName import name1[,name2[, ... nameN]]. For instance, to import the randrange() function from therandom module, we write from random import randrange. To import multiple functions, we separate them with a comma. To import the randrange() and randint() functions, we write from random import randrange, randint. To use the function now, we do not have to use the dot notation anymore. Just write randrange( 1, 10).
# Example 1 of import
%reset -f
import random
low = 1 ; high = 10
random.randrange(low,high) #generate random number in range low to high
# Example 2 of import
%reset -f
import random as r
low = 1 ; high = 10
r.randrange(low,high)
# Example 3 of import
%reset -f
from random import randrange
low = 1 ; high = 10
randrange(low,high)
The modules that come with Python are extensive and listed at https://docs.python.org/3/py-modindex.html. There are also other modules that can be downloaded and used (just like user defined modules below). In these labs we are building primitive codes to learn how to code and how to create algorithms. For many practical cases you will want to load a well-tested package to accomplish the tasks.
That exercise is saved for the end of the document.
User-Built¶
We can define our own functions in Python and reuse them throughout the program. The syntax for defining a function is:
def functionName( argument ):
code detailing what the function should do
note the colon above and indentation
...
...
return [expression]
The keyword def tells the program that the indented code from the next line onwards is
part of the function.
The keyword returntells the program to return an answer from the
function.
There can be multiple return statements in a function.
Once the function executes
a return statement, the program exits the function and continues with its next executable
statement.
If the function does not need to return any value, you can omit the return
statement.
Functions can be pretty elaborate; they can search for things in a list, determine variable types, open and close files, read and write to files.
To get started we will build a few really simple mathematical functions; we will need this skill in the future anyway, especially in scientific programming contexts.
User-built within a Code Block¶
For our first function we will code $$f(x) = x\sqrt{1 + x}$$ into a function named dusty().
When you run the next cell, all it does is prototype the function (defines it), nothing happens until we use the function.
def dusty(x) :
temp = x * ((1.0+x)**(0.5)) # don't need the math package
return temp
# the function should make the evaluation
# store in the local variable temp
# return contents of temp
A simple wrapper script to use the function.
# wrapper to run the dusty function
yes = 0
while yes == 0:
xvalue = input('enter a numeric value')
try:
xvalue = float(xvalue)
yes = 1
except:
print('enter a bloody number! Try again \n')
# call the function, get value , write output
yvalue = dusty(xvalue)
print('f(',xvalue,') = ',yvalue) # and we are done
Exercise 1 (4 points)¶
Create the function $$f(x) = e^x - 10 cos(x) - 100$$ as a function (i.e. use the def keyword)
def name(parameters) :
operations on parameters
...
...
return (value, or null)
Then apply your function to the value.
Use your function to complete the table below:
| x | f(x) |
|---|---|
| 0.0 | |
| 1.50 | |
| 2.00 | |
| 2.25 | |
| 3.0 | |
| 4.25 | |
| 4.50 | |
| 4.75 | |
| 5.00 | |
| 6.00 |
You will reuse the function later in the exercises, so be sure it works.
# define your function here
# build the wrapper here
Variable Scope¶
An important concept when defining a function is the concept of variable scope. Variablesdefined inside a function are treated differently from variables defined outside. Firstly, any variable declared within a function is only accessible within the function. These are known as local variables.
In the dusty() function, the variables x and temp are local to the function.
Any variable declared outside a function in a main program is known as a program variable
and is accessible anywhere in the program.
In the example, the variables xvalue and yvalue are program variables (global to the program; if they are addressed within a function, they could be operated on.)
Generally we want to protect the program variables from the function unless the intent is to change their values.
The way the function is written in the example, the function cannot damage xvalue or yvalue.
If a local variable shares the same name as a program variable, any code inside the function is accessing the local variable. Any code outside is accessing the program variable
As Separate Module/File (Advanced Topic)¶
In this section we will invent the neko() function, export it to a file, so we can reuse it in later notebooks without having to retype or cut-and-paste. The neko() function evaluates:
Its the same as the dusty() function, except operates on the absolute value in the wadical.
- Create a text file named "mylibrary.py"
Copy the neko() function script below into that file.
def neko(input_argument) : import math #ok to import into a function local_variable = input_argument * math.sqrt(abs(1.0+input_argument)) return local_variablemodify the wrapper script to use the neko function as an external module
# wrapper to run the neko function
import mylibrary
yes = 0
while yes == 0:
xvalue = input('enter a numeric value')
try:
xvalue = float(xvalue)
yes = 1
except:
print('enter a bloody number! Try again \n')
# call the function, get value , write output
yvalue = mylibrary.neko(xvalue)
print('f(',xvalue,') = ',yvalue) # and we are done
In JupyterHub environments, you may discover that changes you make to your external python file are not reflected when you re-run your script; you need to restart the kernel to get the changes to actually update. The figure below depicts the notebook, external file relatonship
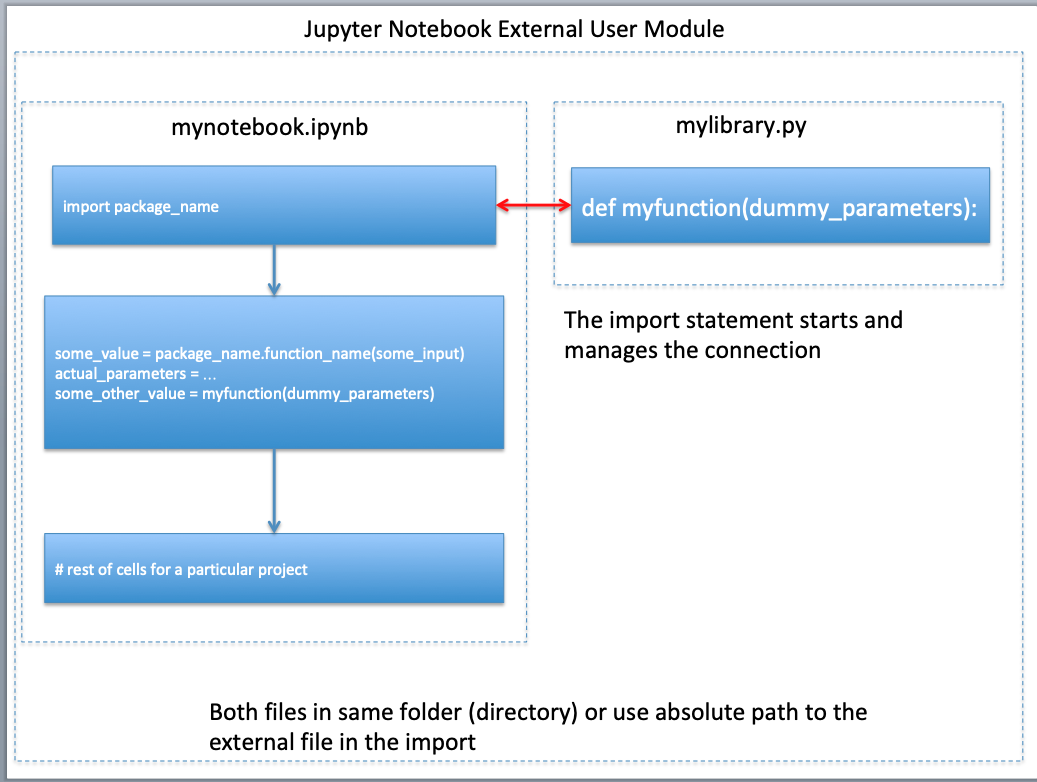
- Future version - explain absolute path
Exercise 1 (Optional, extra credit)¶
Save your function from Exercise 1 into a module; write a wrapper to test the function.
# optional exercise 1 addendum
Rudimentary Graphics¶
Graphing values is part of the broader field of data visualization, which has two main goals:
- To explore data, and
- To communicate data.
In this subsection we will concentrate on introducing skills to start exploring data and to
produce meaningful visualizations we can use throughout the rest of this notebook.
Data visualization is a rich field of study that fills entire books.
The reason to start visualization here instead of elsewhere is that with functions plotting
is a natural activity and we have to import the matplotlib module to make the plots.
The example below is code adapted from Grus (2015) that illustrates simple generic plots. I added a single line (label the x-axis), and corrected some transcription errors (not the original author's mistake, just the consequence of how the API handled the cut-and-paste), but otherwise the code is unchanged.
# python script to illustrate plotting
# CODE BELOW IS ADAPTED FROM:
# Grus, Joel (2015-04-14). Data Science from Scratch: First Principles with Python
# (Kindle Locations 1190-1191). O'Reilly Media. Kindle Edition.
#
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010] # define two lists years and gdp
gdp = [300.2, 543.3, 1075.9, 2862.5, 5979.6, 10289.7, 14958.3]
plt.plot( years, gdp, color ='green', marker ='o', linestyle ='solid') # create a line chart, years on x-axis, gdp on y-axis
plt.title("Nominal GDP")# add a title
plt.ylabel("Billions of $")# add a label to the x and y-axes
plt.xlabel("Year")
plt.show() # display the plot
Now lets put the plotting script into a function so we can make line charts of any two numeric lists
def plotAline(list1,list2,strx,stry,strtitle): # plot list1 on x, list2 on y, xlabel, ylabel, title
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
plt.plot( list1, list2, color ='green', marker ='o', linestyle ='solid') # create a line chart, years on x-axis, gdp on y-axis
plt.title(strtitle)# add a title
plt.ylabel(stry)# add a label to the x and y-axes
plt.xlabel(strx)
plt.show() # display the plot
return #null return
# wrapper
years = [1950, 1960, 1970, 1980, 1990, 2000, 2010] # define two lists years and gdp
gdp = [300.2, 543.3, 1075.9, 2862.5, 5979.6, 10289.7, 14958.3]
print(type(years[0]))
print(type(gdp[0]))
plotAline(years,gdp,"Year","Billions of $","Nominal GDP")
Exercise 2 (2 points)¶
Copy the wrapper script for the plotAline() function, and modify the copy to create a plot of
$$ y = x^2 $$
for x raging from 0 to 9 (inclusive) in steps of 1.
Label the plot and the plot axes.
# Exercise 2 code here
Exercise 3 (4 points)¶
Use your function from Exercise 1. To create a plot of $$f(x)$$ , where $x$ ranges from 0 to 15 in increments of 0.25.
Label the plot and the plot axes.
# Exercise 3 wrapper code here
References¶
Grus, Joel (2015-04-14). Data Science from Scratch: First Principles with Python (Kindle Locations 1190-1191). O'Reilly Media. Kindle Edition.
Call Expressions in "Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science" https://www.inferentialthinking.com/chapters/03/3/Calls.html
Functions and Tables in "Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science" https://www.inferentialthinking.com/chapters/08/Functions_and_Tables.html
Visualization in "Adhikari, A. and DeNero, J. Computational and Inferential Thinking The Foundations of Data Science" https://www.inferentialthinking.com/chapters/07/Visualization.html