Download this page as a jupyter notebook at Lesson 2

%%html
<!-- Script Block to set tables to left alignment -->
<style>
  table {margin-left: 0 !important;}
</style>

%reset -f 

ENGR 1330 Computational Thinking with Data Science

Copyright © 2021 Theodore G. Cleveland and Farhang Forghanparast

Last GitHub Commit Date: 12 August 2021

Lesson 2 Programming Fundamentals:

• iPython, tokens, and structure
• Data types (int, float, string, bool)
• Variables, operators, expressions, basic I/O
• String functions and operations
• How to Build a Notebook (Another look at problem solving)

Programming Fundamentals

Recall the 5 fundamental CT concepts are:

1. Decomposition: the process of taking a complex problem and breaking it into more manageable sub-problems.
2. Pattern Recognition: finding similarities, or shared characteristics of problems to reuse of solution methods ( automation ) for each occurrence of the pattern.
3. Abstraction : Determine important characteristics of the problem and use these characteristics to create a representation of the problem.
4. Algorithms : Step-by-step instructions of how to solve a problem.
5. System Integration: the assembly of the parts above into the complete (integrated) solution. Integration combines parts into a program which is the realization of an algorithm using a syntax that the computer can understand.

Programming is (generally) writing code in a specific programming language to address a certain problem. In the above list it is largely addressed by the algorithms and system integration concepts.

iPython

The programming language we will use is Python (actually iPython). Python is an example of a high-level language; there are also low-level languages, sometimes referred to as machine languages or assembly languages. Machine language is the encoding of instructions in binary so that they can be directly executed by the computer. Assembly language uses a slightly easier format to refer to the low level instructions. Loosely speaking, computers can only execute programs written in low-level languages. To be exact, computers can actually only execute programs written in machine language. Thus, programs written in a high-level language (and even those in assembly language) have to be processed before they can run. This extra processing takes some time, which is a small disadvantage of high-level languages. However, the advantages to high-level languages are enormous:

• First, it is much easier to program in a high-level language. Programs written in a high-level language take less time to write, they are shorter and easier to read, and they are more likely to be correct.
• Second, high-level languages are portable, meaning that they can run on different kinds of computers with just a few modifications.
• Low-level programs can run on only one kind of computer (chipset-specific for sure, in some cases hardware specific) and have to be rewritten to run on other processors. (e.g. x86-64 vs. arm7 vs. aarch64 vs. PowerPC ...)

Due to these advantages, almost all programs are written in high-level languages. Low-level languages are used only for a few specialized applications.

Two kinds of programs process high-level languages into low-level languages: interpreters and compilers. An interpreter reads a high-level program and executes it, meaning that it does what the program says. It processes the program a little at a time, alternately reading lines and performing computations. Recall how an Excel spreadsheet computes from top to bottom, left to right - an interpreted program is much the same, each line is like a cell in a spreadsheet.

As a language, python is a formal language that has certain requirements and structure called "syntax." Syntax rules come in two flavors, pertaining to tokens and structure. Tokens are the basic elements of the language, such as words, numbers, and chemical elements. The second type of syntax rule pertains to the structure of a statement specifically in the way the tokens are arranged.

Tokens and Structure

Consider the relativistic equation relating energy, mass, and the speed of light $$ e = m \cdot c^2 $$

In this equation the tokens are $e$,$m$,$c$,$=$,$\cdot$, and the structure is parsed from left to right as into the token named $e$ place the result of the product of the contents of the tokens $m$ and $c^2$. Given that the speed of light is some universal constant, the only things that can change are the contents of $m$ and the resulting change in $e$.

In the above discourse, the tokens $e$,$m$,$c$ are names for things that can have values -- we will call these variables (or constants as appropriate). The tokens $=$,$\cdot$, and $~^2$ are symbols for various arithmetic operations -- we will call these operators. The structure of the equation is specific -- we will call it a statement.

When we attempt to write and execute python scripts - we will make various mistakes; these will generate warnings and errors, which we will repair to make a working program.

Consider our equation:

#clear all variables# Example 
Energy = Mass * SpeedOfLight**2 

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-9-1c1f1fa5363a> in <module>
      1 #clear all variables# Example
----> 2 Energy = Mass * SpeedOfLight**2

NameError: name 'Mass' is not defined

Notice how the interpreter tells us that Mass is undefined - so a simple fix is to define it and try again

# Example 
Mass = 1000000
Energy = Mass * SpeedOfLight**2 

Notice how the interpreter now tells us that SpeedOfLight is undefined - so a simple fix is to define it and try again

# Example 
Mass = 1000000  #kilograms
SpeedOfLight = 299792458  #meters per second
Energy = Mass * SpeedOfLight**2 

Now the script ran without any reported errors, but we have not instructed the program on how to produce output. To keep the example simple we will just add a generic print statement.

# Example 
Mass = 1000000  #kilograms
SpeedOfLight = 299792458  #meters per second
Energy = Mass * SpeedOfLight**2 
print("Energy is:", Energy, "Newton meters")

Now lets examine our program. Identify the tokens that have values, Identify the tokens that are symbols of operations, identify the structure.

Variables

Variables are names given to data that we want to store, manipulate, and change in programs. A variable has a name and a value. The value representation depends on what type of object the variable represents. The utility of variables comes in when we have a structure that is universal, but values of variables within the structure will change - otherwise it would be simple enough to just hardwire the arithmetic.

Suppose we want to store the time of concentration for some hydrologic calculation. To do so, we can name a variable TimeOfConcentration, and then assign a value to the variable, for instance:

TimeOfConcentration = 0.0

After this assignment statement the variable is created in the program and has a value of 0.0. The use of a decimal point in the initial assignment establishes the variable as a float (a real variable is called a floating point representation -- or just a float).

Naming Rules

Variable names in Python can only contain letters (a - z, A - Z), numerals (0 - 9), or underscores. The first character cannot be a number, otherwise there is considerable freedom in naming. The names can be reasonably long. runTime, run_Time, _run_Time2, _2runTime are all valid names, but 2runTime is not valid, and will create an error when you try to use it.

# Script to illustrate variable names
runTime = 1
_2runTime = 2 # change to 2runTime = 2 and rerun script
runTime2 = 2
print(runTime,_2runTime,runTime2)

There are some reserved words that cannot be used as variable names because they have preassigned meaning in Parseltongue. These words include print, input, if, while, and for. There are several more; the interpreter won't allow you to use these names as variables and will issue an error message when you attempt to run a program with such words used as variables.

Operators

The = sign used in the variable definition is called an assignment operator (or assignment sign). The symbol means that the expression to the right of the symbol is to be evaluated and the result placed into the variable on the left side of the symbol. The "operation" is assignment, the "=" symbol is the operator name.

Consider the script below

# Assignment Operator
x = 5
y = 10
print (x,y)
x=y # reverse order y=x and re-run, what happens?
print (x,y)

So look at what happened. When we assigned values to the variables named x and y, they started life as 5 and 10. We then wrote those values to the console, and the program returned 5 and 10. Then we assigned y to x which took the value in y and replaced the value that was in x with this value. We then wrote the contents again, and both variables have the value 10.

Arithmetic Operators

In addition to assignment we can also perform arithmetic operations on variables. The fundamental arithmetic operators are:

Symbol	Meaning	Example
=	Assignment	x=3 Assigns value of 3 to x.
+	Addition	x+y Adds values in x and y.
-	Subtraction	x-y Subtracts values in y from x.
*	Multiplication	x*y Multiplies values in x and y.
/	Division	x/y Divides value in x by value in y.
//	Floor division	x//y Divide x by y, truncate result to whole number.
%	Modulus	x%y Returns remainder when x is divided by y.
**	Exponentation	x y Raises value in x by value in y. ( e.g. x y)
+=	Additive assignment	x+=2 Equivalent to x = x+2.
-=	Subtractive assignment	x-=2 Equivalent to x = x-2.
*=	Multiplicative assignment	x*=3 Equivalent to x = x*3.
/=	Divide assignment	x/3 Equivalent to x = x/3.

Run the script in the next cell for some illustrative results

# Uniary Arithmetic Operators
x = 10
y = 5
print(x, y)
print(x+y)
print(x-y)
print(x*y)
print(x/y)
print((x+1)//y)
print((x+1)%y)
print(x**y)

# Arithmetic assignment operators
x = 1
x += 2
print(type(x),x)
x = 1
x -= 2
print(type(x),x)
x = 1
x *=3
print(type(x),x)
x = 10
x /= 2
print(type(x),x)  # Interesting what division does to variable type

Data Type

In the computer data are all binary digits (actually 0 and +5 volts). At a higher level of abstraction data are typed into integers, real, or alphanumeric representation. The type affects the kind of arithmetic operations that are allowed (as well as the kind of arithmetic - integer versus real arithmetic; lexicographical ordering of alphanumeric , etc.) In scientific programming, a common (and really difficult to detect) source of slight inaccuracies (that tend to snowball as the program runs) is mixed mode arithmetic required because two numeric values are of different types (integer and real).

Learn more from the textbook

https://www.inferentialthinking.com/chapters/04/Data_Types.html

Here we present a quick summary

Integer

Integers are numbers without any fractional portion (nothing after the decimal point { which is not used in integers). Numbers like -3, -2, -1, 0, 1, 2, 200 are integers. A number like 1.1 is not an integer, and 1.0 is also not an integer (the presence of the decimal point makes the number a real).

To declare an integer in Python, just assign the variable name to an integer for example

MyPhoneNumber = 14158576309

Real (Float)

A real or float is a number that has (or can have) a fractional portion - the number has decimal parts. The numbers 3.14159, -0.001, 11.11, 1., are all floats. The last one is especially tricky, if you don't notice the decimal point you might think it is an integer but the inclusion of the decimal point in Python tells the program that the value is to be treated as a float. To declare a float in Python, just assign the variable name to a float for example

MyMassInKilos = 74.8427

String(Alphanumeric)

A string is a data type that is treated as text elements. The usual letters are strings, but numbers can be included. The numbers in a string are simply characters and cannot be directly used in arithmetic. There are some kinds of arithmetic that can be performed on strings but generally we process string variables to capture the text nature of their contents. To declare a string in Python, just assign the variable name to a string value - the trick is the value is enclosed in quotes. The quotes are delimiters that tell the program that the characters between the quotes are characters and are to be treated as literal representation.

For example

MyName = 'Theodore'
MyCatName = "Dusty"
DustyMassInKilos = "7.48427"

are all string variables. The last assignment is made a string on purpose. String variables can be combined using an operation called concatenation. The symbol for concatenation is the plus symbol +.

Strings can also be converted to all upper case using the upper() function. The syntax for the upper() function is 'string to be upper case'.upper(). Notice the "dot" in the syntax. The operation passes everything to the left of the dot to the function which then operates on that content and returns the result all upper case (or an error if the input stream is not a string).

# Variable Types Example
MyPhoneNumber = 14158576309
MyMassInKilos = 74.8427
MyName = 'Theodore'
MyCatName = "Dusty"
DustyMassInKilos = "7.48427"
print("All about me")
print("Name: ",MyName, " Mass :",MyMassInKilos,"Kg" )
print('Phone : ',MyPhoneNumber)
print('My cat\'s name :', MyCatName)  # the \ escape character is used to get the ' into the literal
print("All about concatenation!")
print("A Silly String : ",MyCatName+MyName+DustyMassInKilos)
print("A SILLY STRING :  ", (MyCatName+MyName+DustyMassInKilos).upper())

Strings can be formatted using the % operator or the format() function. The concepts will be introduced later on as needed in the workbook, you can Google search for examples of how to do such formatting.

Changing Types

A variable type can be changed. This activity is called type casting. Three functions allow type casting: int(), float(), and str(). The function names indicate the result of using the function, hence int() returns an integer, float() returns a oat, and str() returns a string.

There is also the useful function type() which returns the type of variable.

The easiest way to understand is to see an example.

# Type Casting Examples
MyInteger = 234
MyFloat = 876.543
MyString = 'What is your name?'
print(MyInteger,MyFloat,MyString)
print('Integer as float',float(MyInteger))
print('Float as integer',int(MyFloat))
print('Integer as string',str(MyInteger))
print('Integer as hexadecimal',hex(MyInteger))
print('Integer Type',type((MyInteger)))  # insert the hex conversion and see what happens!

Expressions

Expressions are the "algebraic" constructions that are evaluated and then placed into a variable. Consider

x1 = 7 + 3 * 6 / 2 - 1

The expression is evaluated from the left to right and in words is

• Into the object named x1 place the result of:

  integer 7 + (integer 6 divide by integer 2 = float 3 * integer 3 = float 9 - integer 1 = float 8) = float 15

The division operation by default produces a float result unless forced otherwise. The result is the variable x1 is a float with a value of 15.0

# Expressions Example
x1 = 7 + 3 * 6 // 2 - 1  # Change / into // and see what happens!
print(type(x1),x1)
## Simple I/O (Input/Output)

Summary

So far consider our story - a tool to help with problem solving is CT leading to an algorithm. The tool to implement the algorithm is the program and in our case JupyterLab running iPython interpreter for us.

As a formal language we introduced:

• tokens
• structure

From these two constructs we further introduced variables (a kind of token), data types (an abstraction, and arguably a decomposition), and expressions (a structure). We created simple scripts (with errors), examined the errors, corrected our script, and eventually got an answer. So we are well on our way in CT as it applies in Engineering.

How to Build a Program/Notebook

Recall our suggested problem solving protocol:

1. Explicitly state the problem
2. State the input information, governing equations or principles, and the required output information.
3. Work a sample problem by-hand for testing the general solution.
4. Develop a general solution method (coding).
5. Test the general solution against the by-hand example, then apply to the real problem.
6. Refine general solution for deployment (frequent use)

The protocol below is shamelessly lifted from http://users.csc.calpoly.edu/~jdalbey/101/Lectures/HowToBuildAProgram.html here we are using the concept of program and notebook as the same thing.

Building a program is not an art, it is an engineering process. As such there is a process to follow with clearly defined steps.

Analysis (Understand the Requirements)

In this class you will usually be given the problem requirements, unlike the real-world where you have to elicit the requirements from a customer. For you the first step will be to read the problem and be sure you understand what the program must do. Summarize your understanding by writing the Input data, Output data, and Functions (operations or transformation on the data). In the context of our (WCOE) protocol this step comprises Steps 1 and 2.

Create a Test Plan

You must be able to verify that your program works correctly once it is written. Invent some actual input data values and manually compute the expected result. In the context of our (WCOE) protocol this step comprises Steps 3.

Invent a Solution

This is the creative, exploratory part of design where you figure out how to solve the problem. Here is one strategy:

• Solve the problem manually, the way you would do it as a human. Pay careful to attention what operations you perform and write down each step.
• Look for a pattern in the steps you performed.
• Determine how this pattern could be automated using the 3 algorithm building blocks (which we learn about a few lectures from now) (Sequence, Selection, Iteration).

Design (Formalize your solution)

Arrange your solution into components; this is called the architecture. Write the algorithm for each component. Refine your algorithm in a step-wise manner if necessary. Determine the data types and constraints for each data item. Review

Perform a hand trace of your solution and simulate how the computer will carry out your algorithm. Make sure your algorithm works correctly before you put it into the computer.

Implementation (coding)

Translate your algorithm into a programming language and enter it into the computer.
Compile your source code to produce an executable program. You may want to compile and test each subprogram individually before combining them into a complete program.

Testing

Execute the program using the Test Plans you created above. Correct any errors as necessary.

Example of Problem Solving Process

Consider an engineering material problem where we wish to classify whether a material is loaded in the elastic or inelastic region as determined the stress (solid pressure) in a rod for some applied load. The yield stress is the classifier, and once the material yields (begins to fail) it will not carry any additional load (until ultimate failure, when it carries no load).

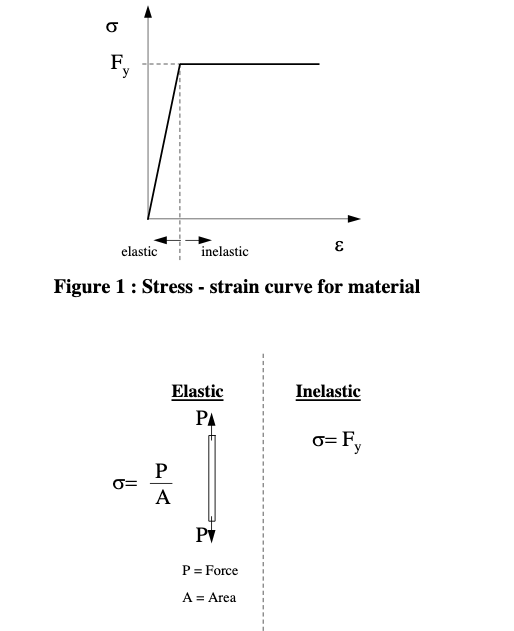
Step 1. Compute the material stress under an applied load; determine if value exceedes yield stress, and report the loading condition

Step 2.

• Inputs: applied load, cross sectional area, yield stress
• Governing equation: $ \sigma = \frac{P}{A} $ when $\frac{P}{A} $ is less than the yield stress, and is equal to the yield stress otherwise.
• Outputs: The material stress $\sigma $, and the classification elastic or inelastic.

Step 3. Work a sample problem by-hand for testing the general solution.

Assuming the yield stress is 1 million psi (units matter in an actual problem - kind of glossed over here)

Applied Load (lbf)	Cross Section Area (sq.in.)	Stress (psi)	Classification
10,000	1.0	10,000	Elastic
10,000	0.1	100,000	Elastic
100,000	0.1	1,000,000	Inelastic

The stress requires us to read in the load value, read in the cross sectional area, divide the load by the area, and compare the result to the yield stress. If it exceeds the yield stress, then the actual stress is the yield stress, and the loading is inelastic, otherwise elastic

$$ \sigma = \frac{P}{A} $$$$ \text{If}~ \sigma >= \text{Yield Stress then report Inelastic} $$

Step 4. Develop a general solution (code)

In a flow-chart it would look like:

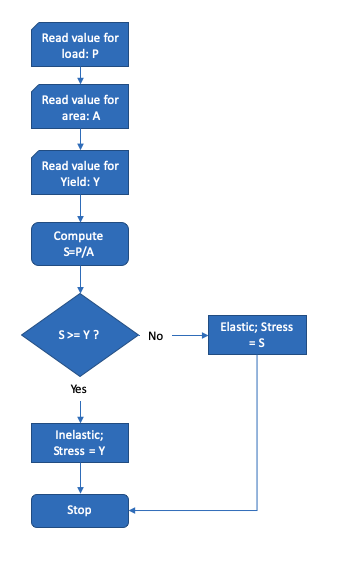
	Flowchart for Artihmetic Mean Algorithm

Step 5. This step we would code the algorithm expressed in the figure and test it with the by-hand data and other small datasets until we are convinced it works correctly. We have not yet learned prompts to get input we simply direct assign values as below (and the conditional execution is the subject of a later lesson)

In a simple JupyterLab script

# Example 2 Problem Solving Process
yield_stress = 1e6
applied_load = 1e5
cross_section = 0.1
computed_stress = applied_load/cross_section
if(computed_stress < yield_stress):
    print("Elastic Region: Stress = ",computed_stress)
elif(computed_stress >= yield_stress):
    print("Inelastic Region: Stress = ",yield_stress)

Step 6. This step we would refine the code to generalize the algorithm. In the example we want a way to supply the inputs by user entry,and tidy the output by rounding to only two decimal places. A little CCMR from https://www.geeksforgeeks.org/taking-input-in-python/ gives us a way to deal with the inputs and typecasting. Some more CCMR from https://www.programiz.com/python-programming/methods/built-in/round gets us rounded out!

# Example 2 Problem Solving Process
yield_stress = float(input('Yield Stress (psi)'))
applied_load = float(input('Applied Load (lbf)'))
cross_section = float(input('Cross Section Area (sq.in.)'))
computed_stress = applied_load/cross_section
if(computed_stress < yield_stress):
    print("Elastic Region: Stress = ",round(computed_stress,2))
elif(computed_stress >= yield_stress):
    print("Inelastic Region: Stress = ",round(yield_stress,2))

So the simple task of computing the stress, is a bit more complex when decomposed, that it first appears, but illustrates a five step process (with a refinement step), and we have done our first classification problem, albeit a very simple case!

Readings

1. Computational and Inferential Thinking Ani Adhikari and John DeNero, Computational and Inferential Thinking, The Foundations of Data Science, Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND) Chapter 3 https://www.inferentialthinking.com/chapters/03/programming-in-python.html

2. Computational and Inferential Thinking Ani Adhikari and John DeNero, Computational and Inferential Thinking, The Foundations of Data Science, Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International (CC BY-NC-ND) Chapter 4 https://www.inferentialthinking.com/chapters/04/Data_Types.html

3. Learn Python in One Day and Learn It Well. Python for Beginners with Hands-on Project. (Learn Coding Fast with Hands-On Project Book -- Kindle Edition by LCF Publishing (Author), Jamie Chan https://www.amazon.com/Python-2nd-Beginners-Hands-Project-ebook/dp/B071Z2Q6TQ/ref=sr_1_3?dchild=1&keywords=learn+python+in+a+day&qid=1611108340&sr=8-3

4. Theodore G. Cleveland, Farhang Forghanparast, Dinesh Sundaravadivelu Devarajan, Turgut Batuhan Baturalp (Batu), Tanja Karp, Long Nguyen, and Mona Rizvi. (2021) Computational Thinking and Data Science: A WebBook to Accompany ENGR 1330 at TTU, Whitacre College of Engineering, DOI (pending)