CE 5364 Groundwater Contaminant Transport Phenomena
Fall 2023 Exam 1 Template
LAST NAME, FIRST NAME
R00000000
Purpose :¶
Demonstrate ability to apply principles of groundwater contaminant transport
Additional Instructions¶
The test is intended to be completed on blackboard. The questions below are transcribed to BB as (in general) file response questions or in the short answer part, as essay response.
Problem 0 (Short Answer)¶
0.1¶
Describe how to use the areal extent of a groundwater contaminant plume with a known source to estimate the local groundwater velocity.
0.2¶
List four transport mechanisms that affect solute migration in groundwater flow.
0.3¶
Why are dispersivity values small (~centimeters) for laboratory column tests and large (~ decameters) for field transport modeling?
0.4¶
List four soil characteristics that affect sorption in groundwater solute transport.
0.5¶
Define natural attenuation as applied in groundwater contamination studies
0.6¶
How does one determine the principal values of the hydraulic conductivity tensor (in 2D)?
0.7¶
What is the practical significance of anisotropy in groundwater contaminant studies?
0.8¶
What is the retardation coefficient?
0.9¶
List four common concentration units
0.10¶
What is the most common chemical contaminant in the world's groundwater and aquifers?
Problem 1 (Problem 2-8, pg. 578)¶
The figure below shows a piezometric map for a shallow sand aquifer with a saturated thickness of 50 ft. The hydraulic conductivity is estimated to be $42~\frac{ft}{day}$.
Determine:
- Which well is expected to be the most contaminated.
- The groundwater velocity and seepage velocity across the plume.
- The duration that the source has been contaminating the aquifer (neglect dispersion, diffusiom, and adsorption).
- The flow rate across the plume.
- An explaination for contamination upgradient of the source zone.
Problem 2 (Problem 2-9, pg 578)¶
Two observation wells 1700 meters apart have been constructed in a confined aquifer with spatially variable hydraulic conductivity as shown below:
The flow rate is 0.008 $\frac{m^3}{hr}$ per unit width (into the plane of the figure) of aquifer. Well 1 is drilled into soil A which has hydraulic conductivity $K = 13 \frac{m}{d}$. Well 2 is drilled into soil B which has hydraulic conductivity $K = 9 \frac{m}{d}$. Soil zone B is between the wells as shown, 600 meters from Well 1 and 300 meters from Well 2. The potentiometric surface is 6 meters above the upper confining unit in Well 1 and 2.5 meters above the upper confining unit in Well 2.
Determine:
- Hydraulic conductivity in Soil B
- Sketch the hydraulic grade line (HGL) from Well 1 to Well 2; clearly indicate the changes in slope in each part of the HGL.
Problem 3 (Problem 2-12, pg. 579)¶
Three geologic formations overlie one another with the characteristics listed below.
$$ b_1 = 50~ft ~~~~ K_1 = 0.0002 \frac{ft}{s}\\ b_2 = 20~ft ~~~~ K_1 = 0.000005 \frac{ft}{s}\\ b_3 = 210~ft ~~~~ K_1 = 0.001 \frac{ft}{s}$$A constant velocity vertical flow field exists across the three formations. The hydraulic head at the top of the formations (top of formation 1) is 33 feet. The hydraulic head at the bottom of the formations (bottom of formation 3) is 21 feet.
Determine:
- Sketch the system.
- The hydraulic head at the internal boundary between formation 1 and 2.
- The hydraulic head at the internal boundary between formation 2 and 3.
Problem 4 (Problem 6-4 pg. 588)¶
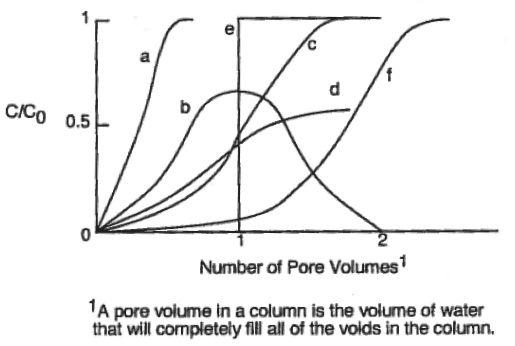
Match the breakthrough curves given in the diagram with the appropriate description given below. Curves represent responses to the injection of a tracer in 1-D soil columns. Choose the best match for each case.
- Curve for a 1-D continuous injection where the constituients get sorbed to the medium
- Curve for a 1-D continuous injection with plug flow is observed
- Curve for an instantaneous source with longitudinal dispersion
- Curve for an instantaneous source with no dispersion
- Curve for a 1-D continuous injection with longitudinal dispersion
- Curve for a 1-D continuous injection with longitudinal dispersion and biodegredation
- Curve for a 1-D continuous injection in which a fracture existed along the soil column
Problem 5 (modified from Problem 6-24 pg. 592)¶
A tank storing various liquids leaks over an area of 10 m$^2$ into an aquifer. One constituient of concern is benzene that is released at a concentration of 10,000 $\frac{\mu~g}{L}$. Assume the aquifer exhibits a retardation factor for benzene of 2.0, and benzene experiences first-order degredation with a decay coefficient $\lambda~=\frac{0.0005}{day}$; the longitudinal dispersion coefficient is $D_l = 1 \frac{m^2}{day}$, the transverse dispersion coefficient is $D_t = 0.1 \frac{m^2}{day}$, the seepage velocity (in longitudinal direction) is $u = 1.0 \frac{m}{day}$.
Determine:
- Time required for the release to traverse 75 meters (ignoring dispersion and degredation)
- Peak concentration at 75 meters
- Approximate plume longitudinal and transverse dimensions at 365 days
Problem 6¶
A one-dimensional column study was conducted using a 30-cm long packed soil column. The injected solute concentration was 10.0 mg/L, and the seepage velocity during the experiment was 0.20 cm/min. The dipsersivity of the solute species in the sample soil is known to be 4.0 cm.
Determine:
- The concentration in mg/L of the solute species in the column effluent 90 minutes after injection began.
Problem 7¶
One kilogram of toluene was spilled into a well that fully penetrates an aquifer. The toluene immediately dissolved and completely mixed into the well water. The well's effective diameter is 0.60 m, and the aquifer has a saturated thickness of 8.5 m; the source area is 5.1 m$^2$. The seepage velocity is 95 m/yr due west, the longitudinal dispersivity is 3.5 m, and the transverse dispersivity is 0.50 m. The aquifer has bulk density of 1.6 g/cc and porosity of 0.40. The distribution coefficient $K_d$ for toluene in the aquifer soil is 0.84 L/kg. Toluene has a first-order decay rate of 0.021 d$^{-1}$
Determine:
- The retardation factor R for toluene in this aquifer.
- The time in years it will take the center of mass of the contaminant plume to travel 5 m in the direction of flow.
- The concentration of toluene in mg/L in a sampling well that is located 5 meters west, and 1.5 meters north of the release point, 3 months from the initial release.