Problem 1 (Problem 11-1, pg. 594)¶
A contaminated site has been surveyed and a contaminated region $100~ft. \times 150~ft. \times 15~ft.$ was delineated. The average concentration of total petroleum hydrocarbons (TPH) in soil is $10,000~\frac{mg}{Kg}$
Determine:
- The total mass of contaminants at the site in kilograms. Assume the soil has a specific gravity, $SG _{soil} \approx 2.0$
- Estimate total volume of petroleum hydrocarbons released assuming 50% of the hydrocarbins are lost to volatization, biodegredation, and dissolution (report the answer in gallons). Assume the hydrocarbons were gasoline with a constant specific gravity, $SG_{\text{gasoline}} \approx 0.8$
- Estimate the residual saturation of the hydrocarbon-soil system. Assume soil porosity is, $n=0.35$
# Enter your solution below, or attach separate sheet(s) with your solution.
iZV = 100*150*15
impacted_zone_volume = iZV/(3.28**3) # convert to cubic meters
print("Impacted Zone Volume : ",round(impacted_zone_volume,1)," cubic meters ")
tph = 10000 # mg/Kg
rho_soil = 2.0*1000 #Kg/m^3
rho_tph = 0.8*1000 #Kg/m^3
mass_soil_impacted = rho_soil*impacted_zone_volume
mass_tph = tph*mass_soil_impacted*(1/1000)*(1/1000) # convert to kilograms
loss_fraction = 0.50 # HC losses
volume_soil_tph = mass_tph/rho_tph
volume_release_tph = volume_soil_tph/loss_fraction
volume_release_tph = volume_release_tph*(3.28**3)*7.48 # convert m^3 to gallons
print("Mass Soil Impacted : ",round(mass_soil_impacted,1)," kilograms ")
print("Mass TPH in soil : ",round(mass_tph,2)," kilograms ")
print("Initial TPH Volume : ",round(volume_release_tph,1)," gallons ")
porosity = 0.35
pore_volume = porosity*impacted_zone_volume
saturation_tph = volume_soil_tph/pore_volume
print("Impacted Zone Pore Volume : ",round(pore_volume,1)," cubic meters ")
print("TPH saturation in soil : ",round(saturation_tph,2)," ")
Problem 2 (Problem 11-2, pg. 594)¶
A sampling program at a Supermanfund site indicated the following DNAPL zones:
- A pool of free phase DNAPL in a stratigraphic depression in an unfractured clay. The pool is 200 $ft^2$ in area and 5 $ft$ thick.
- A zone of residual DNAPL extending directly underneath an old disposal pit 100 $ft^2$ in area. The residual zone extends through the 5 $ft$ thick unsaturated zone and 15 $ft$ through the saturated zone until it reaches the DNAPL pool.

Supporting data:
| Residual saturation in the unsaturated zone: | 0.10 |
| Residual saturation in the saturated zone: | 0.35 |
| Saturation in the free-phase zone: | 0.70 |
| Average porosity in water zone: | 0.30 |
Determine:
- The total volume of DNAPL at the site
- The recoverable volume using ordinary pumping.
# Enter your solution below, or attach separate sheet(s) with your solution.
Assuming the clay portion depicted has porosity of 50%
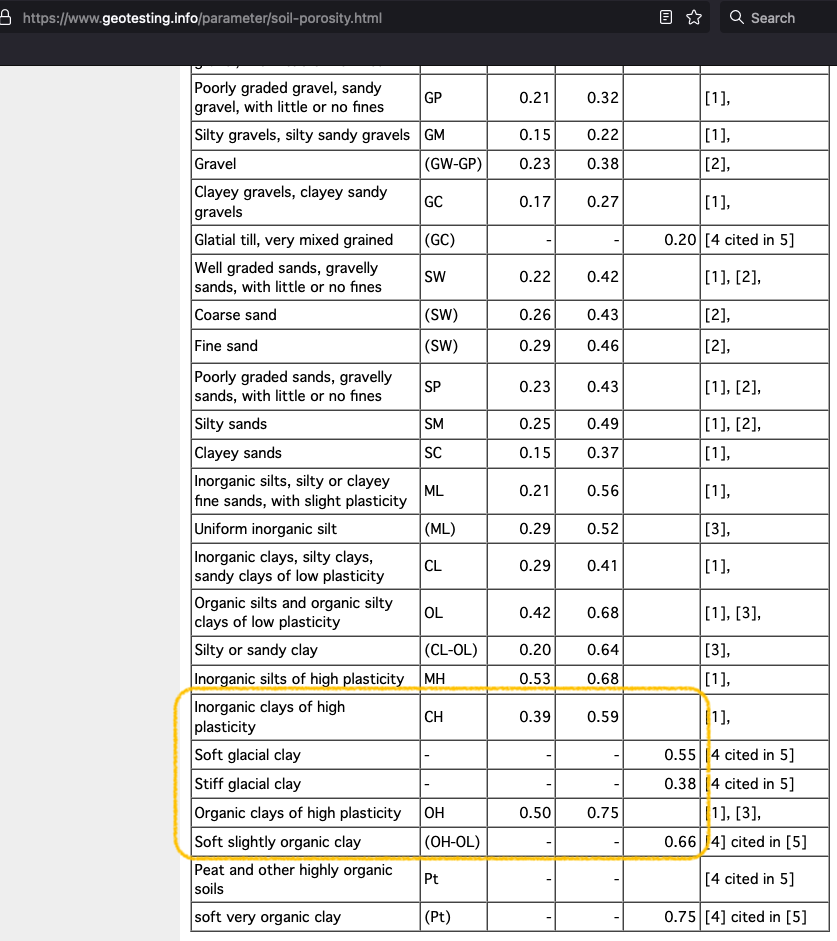
dnapl_pool_vol = 0.5*200*5 # cubic feet
pore_volume_unsat = 0.30*100*5 # cubic feet
pore_volume_sat = 0.30*100*15 # cubic feet
dnapl_unsat = 0.10*pore_volume_unsat
dnapl_sat = 0.35*pore_volume_sat
total_dnapl = dnapl_pool_vol+dnapl_unsat+dnapl_sat
print("DNAPL free phase volume : ",round(dnapl_pool_vol,1)," cubic feet")
print("DNAPL unsaturated zone volume : ",round(dnapl_unsat,1)," cubic feet")
print("DNAPL saturated zone volume : ",round(dnapl_sat,1)," cubic feet")
print("DNAPL total volume : ",round(total_dnapl,1)," cubic feet")
Recoverable volume:
Using something like:
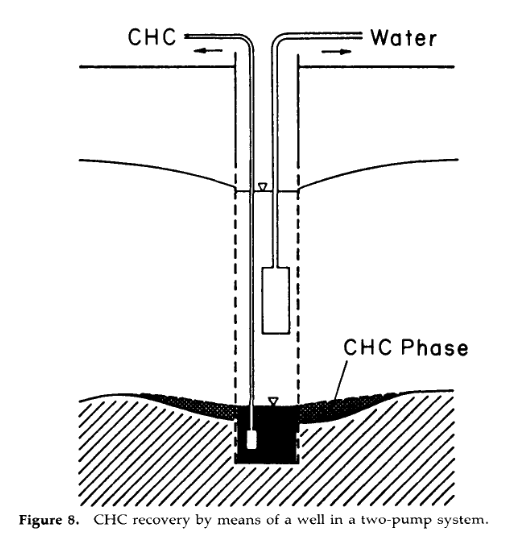
One could only expect to recover from the free phase pool. Assuming the clay goes to a residual similar to the saturated zone (35% of the pore volume contains NAPL)
pore_volume_clay = dnapl_pool_vol
unrecoverable = pore_volume_clay*0.35
recoverable = pore_volume_clay - unrecoverable
print("DNAPL recoverable volume : ",round(recoverable,1)," cubic feet")
Problem 3 (Problem 11-4, pg. 595)¶
Gasoline is found in a monitoring well with $SG=0.80$. A total depth of 6 $ft$ of gasoline is found in the well.
Determine:
- Estimated thickness of free-phase LNAPL in the formation.
# Enter your solution below, or attach separate sheet(s) with your solution.
Sketch situation
Apply equation 11.18 as follows:
head_well = 6.0 # feets
rho_napl = 0.8*62.4 # lbf/ft^3
rho_water = 1.00*62.4 # lbf/ft^3
head_formation = head_well*(rho_water-rho_napl)/rho_napl
print(" NAPL formation thickness : ",round(head_formation,1)," feet ")