CE 4363/5363 Groundwater Hydrology
Spring 2023 Exam 2
LAST NAME, FIRST NAME
R00000000
Purpose :¶
Demonstrate ability to apply groundwater hydrology principles to aquifers
Additional Instructions¶
- The test is intended to be completed by extracting the problem statements and inserting worked answers, including computations into a document, saving that document as a PDF file, and uploading the completed exam to Blackboard.
- Show your work; handwritten is OK, but must be neat, organized, and legible (no brain vomit)
- Cite reference sources used to support your work
CE 4363 Complete problems 1-4
CE 5363 Complete problems 1-6
Problem 7 is extra credit for either course
Question 2 (30 pts.)¶
A confined aquifer system is conceptualized as pictured below.
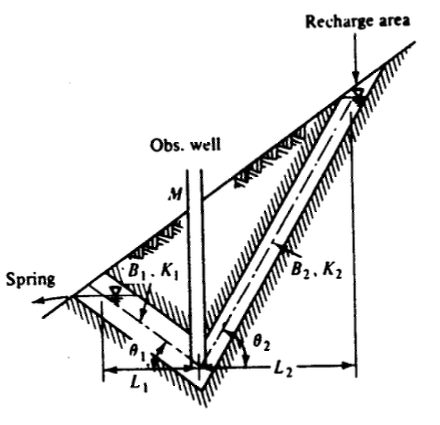
Water enters the system in the recharge area and exits as a spring.
Determine:
- The piezometric head in the well located at $M$ (express the head in terms of the other variables indicated on the sketch)
- Specify the conditions for the well to become a flowing (artesian) well (water flows from the well without pumping).
Question 3 (30 pts.)¶
A 4-cell aquifer model is conceptualized in the figure below.
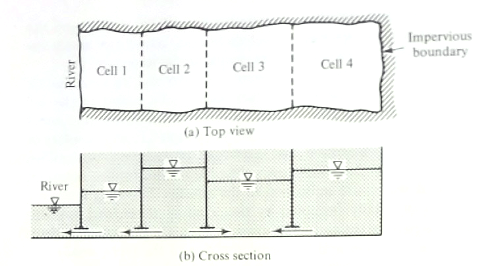
The width of the aquifer strip is 3.0 km; the length of each cell is 5 km. The recharge rates for the aquifer strip is $400~\frac{mm}{yr}$, $300~\frac{mm}{yr}$,$300~\frac{mm}{yr}$, $200~\frac{mm}{yr}$ in Cells 1,2,3, and 4, respectively. The water level in the river is maintained at a constant elevation of $160~m$ above the horizontal impervious bottom. The hydraulic conductivity in Cells 1 and 2 is $3~\frac{m}{d}$, while in Cells 3 and 4 it is $6~\frac{m}{d}$.
Using this conceptual model, determine:
- Write the steady-flow balance equations to estimate average water levels in the four cells.
- Solve these equations to determine the average elevations in the 4 cells without pumping.
- Solve these equations when pumping takes place in Cells 2 and 3 at rates of $4\times10^{6}~\frac{m^3}{yr}$ and $7\times10^{6}~\frac{m^3}{yr}$, respectively.
Reference(s)¶
- Bear (1979). Hydraulics of Groundwater McGraw-Hill (Chapter 10: Modeling of Aquifer Systems) (Eq. 10-9) is useful.
Question 4 (30 pts.)¶
The figure is a plan view of a confined aquifer showing two contaminated zones, 1 and 2. The aquifer has a saturated thickness of 80 ft, hydraulic conductivity of 42 ft/d, and the regional hydraulic gradient is 0.0075 from right to left as shown. A pumping well with a flow rate of 170 gpm is planned to run continuously at the location shown, and form a stable (equilibrium) capture zone. You may assume that the 2500 ft distance from the well to zone 1 is long enough that the capture zone has reached its maximum width.
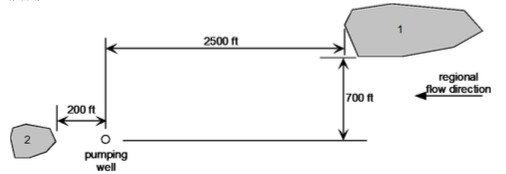
Determine:
- If contamination from zone 1 find its way to the pumping well? Provide support for your answer with a capture zone analysis or contaminant simulation model.
- If contamination from zone 2 find its way to the pumping well? Provide support for your answer with a capture zone analysis or contaminant simulation model.
References¶
CE 5363 Question 5 (30 pts.)¶
A saturated aquifer sample core of diameter 2.54 cm and length of 6 cm weighs 63 grams. After drying the sample weighs 53 grams. The core sample was placed into an permeameter and exposed to a unit hydraulic gradient. The measured flowrate was 25.4 milliliters/second.
The water levels in three wells in the same aquifer were measured in meters above MSL. The levels were: Well MW-1: 83.1 m; Well MW-2: 84.6 m; Well MW-3: 83.9 m.
Well MW-2 is located 1km due north of Well MW-1, and Well MW-3 is located 700 meters Northeast of Well MW-1.
Determine:
- Estimate the porosity of the aquifer.
- Estimate the hydraulic conductivity of the aquifer.
- Sketch the relative positions of the three wells. Use MW-1 as the origin of the local (your sketch) coordinate system, and North is to the top of your sketch.
- Determine the magniture and direction of the hydraulic gradient in the aquifer monitored by the three wells. Indicate the hydraulic gradient on your sketch (direction and magnitude)
- Estimate the concentration of a conservative constituient (contaminant) at a receptor 4 km away from MW-1 on a flowline that passes through MW-1 using the Ogata-Banks model, assuming MW-1 is at the source location, and the source concentration is 1000 mg/l. Use one-tenth of the path length as the aquifer dispersivity (recall dispersion coefficient is the product of dispersivity and average linear velocity). Calculate the receptor concentration from 0 days after release to 1000 days after release in 10 day increments, and make a concentration history plot for the receptor location.
- An estimate of the time from release until the concentration at the receptor is 500 mg/L.
References¶
CE 5363 Question 6 (15 pts.)¶
The three figures below depict streamline patterns for flow near a circular region.
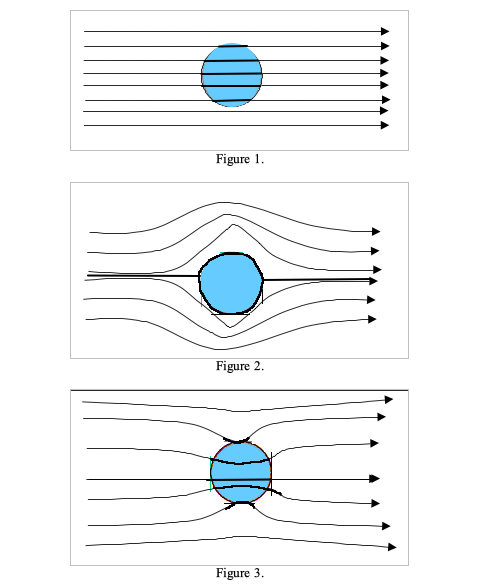
Explain the differences in the patterns in terms of the hydraulic conductivity within the circular region and the surrounding region.
CE 4363/5363 Question 7 (Extra Credit) (30 pts.)¶
Consider a single “cell” model. The cell contains a liquid with known initial concentration of a pollutant. The cell is flushed at a constant flow rate with a liquid with zero concentration of the pollutant.
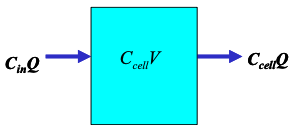
The cell is completely back-mixed, so any mass entering is uniformily distributed within the cell. The volume of the cell is $V$, the discharge entering and leaving is $Q$
Determine:
- An expression for the mass of pollutant in the cell at any time.
- A difference expression for the change in mass in the cell over a discrete time interval (∆t).
- The mass flow of pollutant into the cell (yes, I know its zero, but play along).
- The mass flow of pollutant leaving the cell.
- Combine 2,3, and 4 into a single balance expression (i.e. $\frac{\Delta C}{\Delta t} = \dots~$).