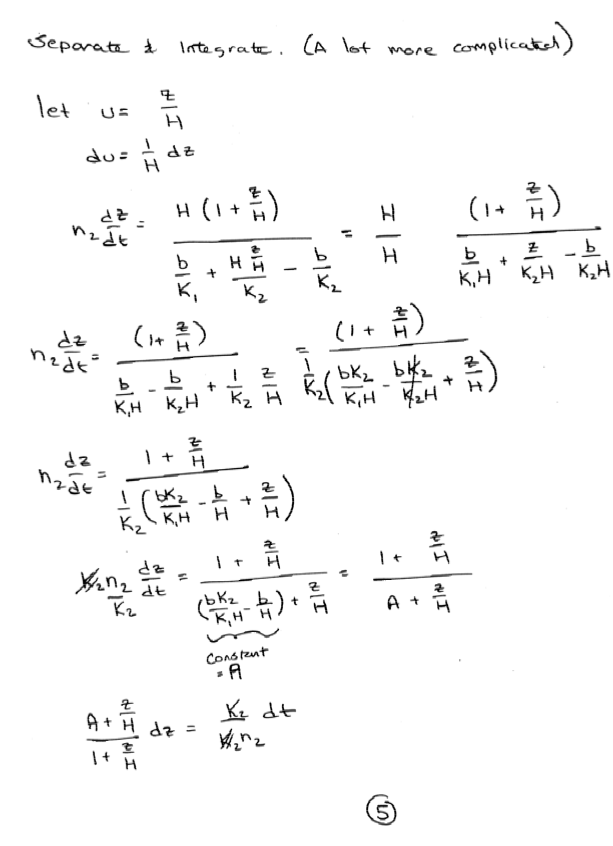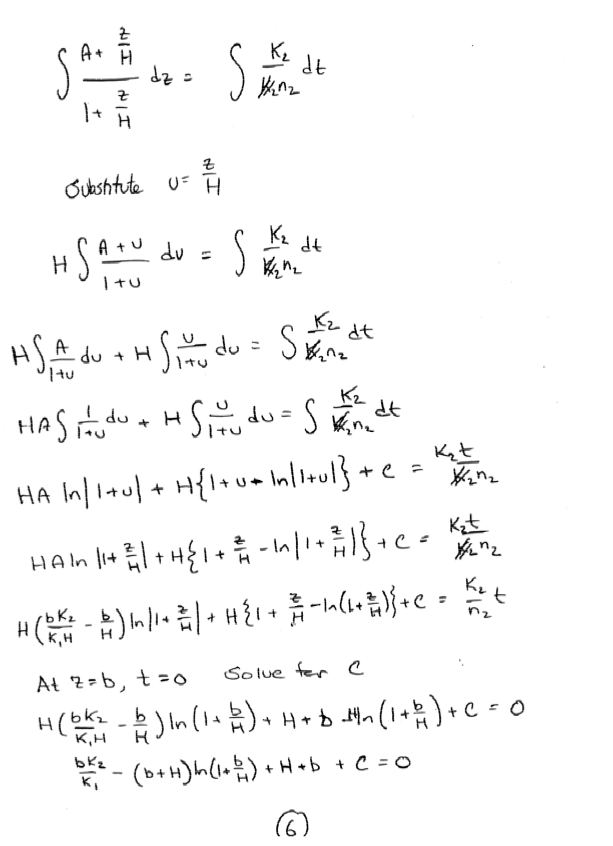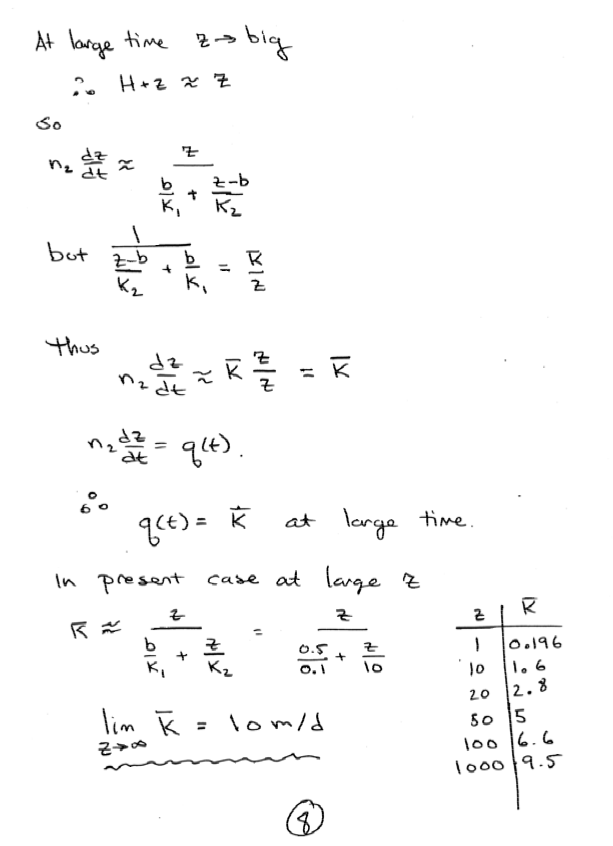CE 4363/5363 Groundwater Hydrology
Spring 2023 Exam 1
LAST NAME, FIRST NAME
R00000000
Purpose :¶
Demonstrate ability to apply groundwater hydrology principles to aquifers
Additional Instructions¶
- The test is intended to be completed by extracting the problem statements and inserting worked answers, including computations into a document, saving that document as a PDF file, and uploading the completed exam to Blackboard.
- Show your work; handwritten is OK, but must be neat, organized, and legible (no brain vomit)
- Cite reference sources used to support your work
CE 4363 Complete problems 1-10
CE 5363 Complete problems 1-15
Question 1 (1 pts.)¶
An aquitard is
- is a low-permeability geologic unit that can store groundwater and transmit it slowly from one aquifer to another.
- is an impermeable geologic unit
- a geologic unit which is neither porous nor permeable
- a saturated geologic unit that stores and transmits water in useful quantities
Solution
An aquitard is a layer of earth or rock that restricts the flow of water between two aquifers. Unlike an aquifer, which is a layer of earth or rock that can store and transmit water, an aquitard has low permeability and acts as a barrier to water flow. While an aquitard may contain water, it cannot transmit it easily due to its low permeability. Aquitards can play an important role in groundwater management, as they can help regulate the movement and distribution of water in aquifers.
From this definition (1) is the bestest answer.
Reference¶
Chat GPT 3.0 Completion An aquitard is ...
Question 2 (1 pts.)¶
An aquifer is
- is a low-permeability geologic unit that can store groundwater and transmit it slowly from one aquifer to another.
- is an impermeable geologic unit
- a geologic unit which is neither porous nor permeable
- a saturated geologic unit that stores and transmits water in useful quantities
Solution
An aquifer is an underground layer of permeable rock, sediment, or soil that can hold and transmit water. It is a natural storage and conveyance system for groundwater. When precipitation or surface water infiltrates the ground, it moves through the pores and spaces in the rock or soil until it reaches an impermeable layer or a surface water body such as a lake, river, or ocean. The water stored in aquifers can be extracted by drilling wells, and it is an important source of drinking water for many communities around the world. However, overuse of aquifers can lead to depletion and contamination of the groundwater.
From this definition (4) is the bestest answer.
Reference¶
Chat GPT 3.0 Completion An aquifer is ...
Question 3 (3 pts.)¶
Explain why the bottom of the aquifer is always used as the datum for head calculations when dealing with unconfined aquifers.
Solution
The bottom of the aquifer is always used as the datum for head calculations when dealing with unconfined aquifers because the water table in unconfined aquifers is free to move up and down, depending on factors such as precipitation, evapotranspiration, and groundwater pumping. The water table represents the upper surface of the groundwater in an unconfined aquifer, and its elevation is a measure of the hydraulic head of the groundwater at that location.
The hydraulic head is the potential energy per unit weight of water at a particular location in an aquifer, and it determines the direction and rate of groundwater flow. The hydraulic head is measured from a reference point or datum, which is typically chosen as the bottom of the aquifer. This is because the bottom of the aquifer represents the lowest point that the water table can fall to under natural conditions, and it is a fixed reference point that does not change over time.
Using the bottom of the aquifer as the datum for head calculations allows hydrogeologists and engineers to measure and monitor changes in the hydraulic head at different locations in the aquifer and assess the impact of various factors, such as groundwater pumping or changes in land use, on the groundwater system. It also allows them to make accurate predictions of groundwater flow rates and direction and design effective groundwater management strategies to protect this vital resource.
Reference¶
Chat GPT 3.0 Completion Explain why the bottom of the aquifer is always used as the datum for head calculations when dealing with unconfined aquifers.
Question 4 (5 pts.)¶
What volume of solid material is present in one cubic meter of sandstone if the porosity is 20% ?
Solution
If the porosity of sandstone is 20%, it means that 20% of the volume is composed of voids or empty space, while the remaining 80% is composed of solid material.
Therefore, the volume of solid material in one cubic meter of sandstone can be calculated as:
Volume of solid material = 80% of 1 cubic meter
Volume of solid material = 0.8 x 1 cubic meter
Volume of solid material = 0.8 cubic meters
So, there is 0.8 cubic meters of solid material present in one cubic meter of sandstone if the porosity is 20%.
Reference¶
Chat GPT 3.0 Completion What volume of solid material is present in one cubic meter of sandstone if the porosity is 20% ? )
Question 5 (5 pts.)¶
What volume of water is contained in one cubic meter of material if the porosity is 20% and the saturation expressed as a fraction of the pore space is 30% ?
Solution
If the porosity of a material is 20%, it means that 20% of its total volume is made up of pore space (voids). Therefore, the remaining 80% of the volume is made up of solid material.
If the saturation expressed as a fraction of the pore space is 30%, it means that 30% of the pore space is filled with water, while the remaining 70% is empty.
To find the volume of water contained in one cubic meter of the material, we can use the following formula:
Volume of water = Porosity x Saturation x Total volume
where the total volume is equal to one cubic meter.
Plugging in the values we have:
Volume of water = 0.20 x 0.30 x 1
Volume of water = 0.06 cubic meters
Therefore, one cubic meter of the material contains 0.06 cubic meters (or 60 liters) of water.
Reference¶
Chat GPT 3.0 Completion What volume of water is contained in one cubic meter of material if the porosity is 20% and the saturation expressed as a fraction of the pore space is 30% ?
Question 6 (5 pts.)¶
During a long drought period the following declines in the water table were recorded in an unconfined aquifer.
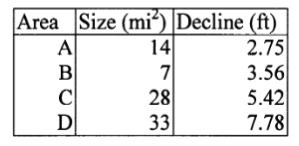
The total volume of water removed from storage in this aquifer during the time period was $5.7385 \times 10^4$ acre-feet.
Determine:
- The specific yield of this aquifer
Solution
Apply same method as in ES1-2, compute volume from each cell using assumed Sy, total volume dewatered must equal withdrawl, answer is $S_y=0.19$
identity = ["A","B","C","D"] #given
size = [14.0,7.0,28.0,33.0] #given
deltah = [2.75,3.56,5.42,7.78] #given
Sy = 0.19 #unknown, trial-and-error this value
target = 5.7385e04 #given total withdrawl in ac-ft
volume = [0 for i in range(len(identity))]
for i in range(len(identity)):
volume[i]=Sy*deltah[i]*size[i]*5280*5280 #convert mi^2 to ft^2
total = sum(volume)/43560
print("Sy guess",round(Sy,4))
print("Target withdrawl",round(target,3),"acre-feet")
print("Total withdrawl",round(total,3),"acre feet")
print("Mass Balance Error",round(100*(total - target)/target,3),"percent")
print("If Total > Target, reduce Sy value")
Question 6 (15 pts.)¶
Three wells are completed in an aquifer in the configuration shown below. Well C is directly east of Well B. The land surface elevations and depths to water are shown in the table.
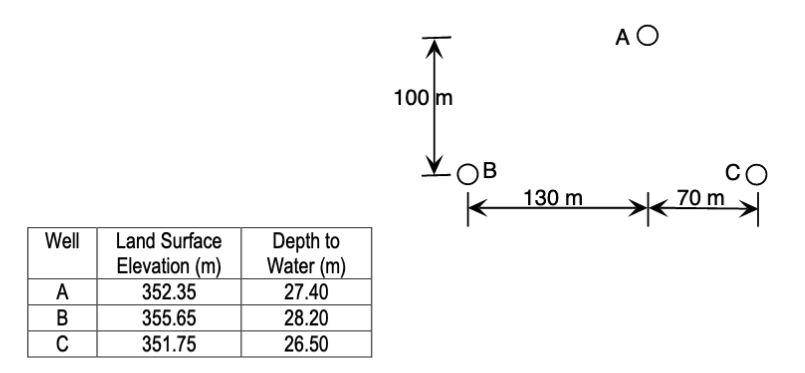
Determine:
- The magnitude and direction of the hydraulic gradient.
Solution
Same as ES2-5
import numpy
import math
# well B is origin
wellID =['Well A','Well B','Well C']
well_X =[130.0,0.0,200.0]
well_Y =[100.0,0.0,0.0]
well_Z =[352.35-27.40,355.65-28.20,351.75-26.50]
amatrix = [[0 for j in range(3)]for i in range(3)]
b = [0 for j in range(3)]
# A-matrix
for i in range(3):
amatrix[i][0]=well_X[i]
amatrix[i][1]=well_Y[i]
amatrix[i][2]=1.0
b[i]= well_Z[i]
amatrix = numpy.array(amatrix) #typecast as numpy array
b = numpy.array(b)
x = numpy.linalg.solve(amatrix,b) # solve equation of plane
# recover and report results
print("x-component hydraulic gradient: ",round(-x[0],3))
print("y-component hydraulic gradient: ",round(-x[1],3))
grad = math.sqrt(x[0]**2+x[1]**2)
print("magnitude hydraulic gradient: ",round(grad,3))
print("direction cosine x-component hydraulic gradient: ",round(-x[0]/grad,3))
print("direction cosine y-component hydraulic gradient: ",round(-x[1]/grad,3))
# angle in radians
angle = math.atan(x[1]/x[0])
# convert to degrees
print("Gradient azmiuth",round(180*angle/math.pi,1),"degrees (0 is due North in the plot)")
# use this if want to plot
list1 = [0,-100*x[0]/grad]
list2 = [0,-100*x[1]/grad]
stry='Distance Northing'
strx='Distance Easting'
strtitle='Hydraulic Gradient and 3-Well Locations\n'+'Gradient Magnitude: '+ str(round(grad,3)) +'\n Red segment is 100X direction cosines'
plotlabel=['Wells','Gradient']
from matplotlib import pyplot as plt # import the plotting library from matplotlibplt.show()
plt.plot(well_X, well_Y, color ='green', marker ='o', linestyle ='none') # create a line chart, years on x-axis, gdp on y-axis
plt.plot(list1, list2, color ='red', marker ='x', linestyle ='solid')
plt.title(strtitle)# add a title
plt.ylabel(stry)# add a label to the x and y-axes
plt.xlabel(strx)
plt.legend(plotlabel)
plt.grid()
plt.show() # display the plot
Question 7 (15 pts.)¶
A single well exists in an ideal unconfined aquifer. The pumping well has a flow rate of 200 gpm and an effective well radius of 0.60 ft. An observation well was placed 85 ft away from the centerline of the pumping well. The pumping well has been on long enough for equilibrium to be achieved, and drawdowns at the two wells were as shown in the figure below. The sketch is not to scale.
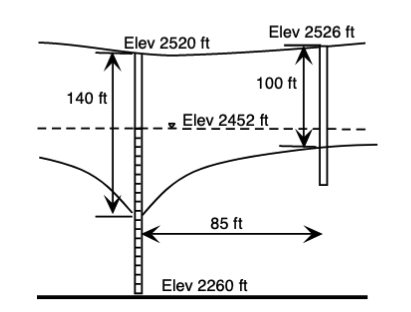
Determine:
- The hydraulic conductivity of the aquifer in $\frac{ft}{d}$.
- The radius of influence for this pumping well in $ft$.
Solution
Apply Theim equation for unconfined aquifer, solve for K. Then find distance until no drawdown for radius-o-influence.
# Saturated thickness pre-development
# pumpin well
PGLp = 2520
HGLp= 2452
Bot= 2260
# observation well
PGLo = 2526
HGLo = 2452
h1 = (PGLp - Bot)-140
h2 = (PGLo - Bot)-100
print(" Head in pumping well ",h1," feet above bottom of aquifer")
print("Head in observation well ",h2," feet above bottom of aquifer")
# Theim equation unconfined
h1 = 120 #calculated
h2 = 166 #calculated
r1 = 0.60 #given raduis at well screen
r2 = 85 #given distance to observation well
QGPM = 200 #given
QCFS = QGPM*(1.0/7.485)*(1.0/60.0) #gpm to cfs
QCFD = QCFS*86400 #cfs to cfday
K = (QCFD/(math.pi*(h2**2-h1**2)))*math.log(r2/r1)
print("Hydraulic Conductivity = ",round(K,3)," ft/day ")
# Find effective radius
h2target = HGLp-Bot
r2 = 2828 # guess value, adjust by trial-and-error
(h2guess)=math.sqrt((h1**2)+(QCFD/(math.pi*K))*math.log(r2/r1))
print("Target",round(h2target,3),"Guess",round(h2guess,3),"Diffence ",round(h2target-h2guess,3))
So the hydraulic conductivity is $K=4.611~\frac{ft}{day}$ and the radius of influence is $2828~meters$
Question 8 (15 pts.)¶
A conventional pumping test was performed in an ideal confined aquifer under all the proper conditions. The flow rate at the pumping well was 100 gpm, and the distance to the pumping well was 170 ft. The drawdown observed at the pumping well is shown in the table below.
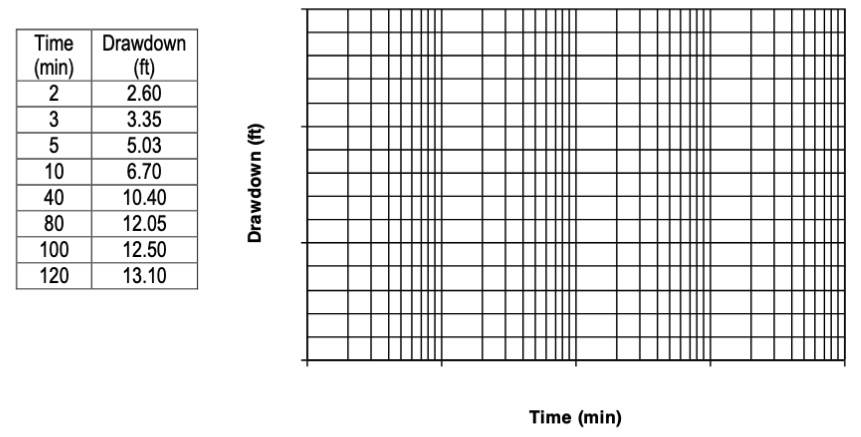
Determine:
- Drawdown vs Time on the semi-logarithmic chart (see Fetter pg. 181)
- The transmissivity in $\frac{ft^2}{d}$, and storage coefficient for this aquifer.
Solution
Use tools developed in ES3-
def W(u): # Theis well function using exponential integral
import scipy.special as sc
w = sc.expn(1,u)
return(w)
def smodel(radius,time,storage,transmissivity,discharge): # Drawdown function using exponential integral
import math
u = ((radius**2)*(storage))/(4*transmissivity*time)
smodel = ((discharge)/(4*math.pi*transmissivity))*W(u)
return(smodel)
data = [\
[2,170,2.60],\
[3 ,170,3.35],\
[5 ,170,5.03],\
[10 ,170,6.70],\
[40 ,170,10.40],\
[80 ,170,12.05],\
[100 ,170,12.50],\
[120 ,170,13.10]\
]
S = 0.01 # initial guess - use a minSSE search to find good value
T = 1000.0 # ft^2/day guess - use a minSSE search to find good value
QGPM = 100 # given
QCFD = QGPM*(1/7.48)*(1440/1) # convert to ft^3/day
ddn = [0 for i in range(len(data))]
ddnobs = [0 for i in range(len(data))]
time = [0 for i in range(len(data))]
distance = [0 for i in range(len(data))]
print("Input Data and Initial Guess")
print("Transmissivity :",round(T,3)," ft^2/day \nStorativity :",round(S,6))
print("Time(days)|Radius(ft)|Obs. Drawdown(ft)|Mod. Drawdown(ft)|")
sse = 0.0
for irow in range(len(data)):
time[irow]=data[irow][0]
distance[irow]=data[irow][1]
ddnobs[irow]=data[irow][2]
ddn[irow] = smodel(distance[irow],time[irow]/1440,S,T,QCFD)
print("%10i|%10i|%17.2f|%17.2f|"%(time[irow],distance[irow],round(ddnobs[irow],2),round(ddn[irow],2)))
sse = sse + (ddnobs[irow]-ddn[irow])**2
print("Initial Sum Squared Error :",round(sse,6))
# plotting results
# import the package
from matplotlib import pyplot as plt
graph, (plt1) = plt.subplots(1, 1) # create a 1X1 plotting frame
plt1.plot(time, ddn, c='blue',linewidth=1) # basic line plot
plt1.plot(time, ddnobs, c='red', marker='o',linewidth=0) # basic line plot
plt1.set_xscale('log') # set x-axis to display a logarithmic scale #################
plt1.set_xlabel('Time (ft)') # label the x-axis
plt1.set_ylabel('Drawdown (ft)') # label the y-axis, notice the LaTex markup
plt1.legend(['Model','Observed']) # legend for each series
plt1.set_title('Drawdown vs Time at Distance: ' + str(distance[0]) + " feet\n" + "Sum Squared Error: " + str(round(sse,6))) # make a plot title
plt1.grid() # display a grid
plt.show() # display the plot
So the initial guess barely even plots on the data chart. Now by changing T and S we try to make the blue line pass through the red dots. Can try by trial-and-error, or just use calculus and some programming.
# build an optimizer to automatically find T and S
import numpy as np
from scipy.optimize import minimize
from scipy.optimize import Bounds
import math
def objfn(x):
global data,ddn,ddnobs,time,distance
global QCFD
T = x[1]
S = x[0]
sse = 0.0
for irow in range(len(data)):
time[irow]=data[irow][0]
distance[irow]=data[irow][1]
ddnobs[irow]=data[irow][2]
ddn[irow] = smodel(distance[irow],time[irow]/1440,S,T,QCFD)
# print("%10i|%10i|%17.2f|%17.2f|"%(time[irow],distance[irow],round(ddnobs[irow],2),round(ddn[irow],2)))
sse = sse + (ddnobs[irow]-ddn[irow])**2
return(sse)
bounds = Bounds([0.0000001, 0.01], [1.0, 10000.0]) # define the search region
ineq_cons = {'type': 'ineq'} # null inequality constraints
eq_cons = {'type': 'eq',} # null equality constraints
x0 = np.array([S, T]) # initial guess
res = minimize(objfn, x0, method='SLSQP', jac="2-point", options={'ftol': 1e-16},bounds=bounds)
if res.status == 0: # success then extract and print the results
T = res.x[1]
S = res.x[0]
# report results
print("Input Data and Fitted Model")
print("Transmissivity :",round(T,1)," ft^2/day \nStorativity :",round(S,6))
print("Time(days)|Radius(ft)|Obs. Drawdown(ft)|Mod. Drawdown(ft)|")
for irow in range(len(data)):
time[irow]=data[irow][0]
distance[irow]=data[irow][1]
ddnobs[irow]=data[irow][2]
ddn[irow] = smodel(distance[irow],time[irow]/1440,S,T,QCFD)
print("%10i|%10i|%17.2f|%17.2f|"%(time[irow],distance[irow],round(ddnobs[irow],2),round(ddn[irow],2)))
# plotting results
# import the package
from matplotlib import pyplot as plt
graph, (plt1) = plt.subplots(1, 1) # create a 1X1 plotting frame
plt1.plot(time, ddn, c='blue',linewidth=1) # basic line plot
plt1.plot(time, ddnobs, c='red', marker='o',linewidth=0) # basic line plot
plt1.set_xscale('log') # set x-axis to display a logarithmic scale #################
plt1.set_xlabel('Time (ft)') # label the x-axis
plt1.set_ylabel('Drawdown (ft)') # label the y-axis, notice the LaTex markup
plt1.legend(['Model','Observed']) # legend for each series
plt1.set_title('Drawdown vs Time at Distance: ' + str(distance[0]) + " feet\n" + "Sum Squared Error: " + str(round(res.fun,6))) # make a plot title
plt1.grid() # display a grid
plt.show() # display the plot
Ta da! - we have a decent fit. Type curves would be fine too, as would Jacob's approximation.
Question 9 (15 pts.)¶
Two boreholes are located at points A and B along the same flowline. The soil between them has a hydraulic conductivity of $3.0 \times 10^{-5}$ feet per second and a porosity of 40%. Water flows from B to A in the water table aquifer. A 500 X 100 foot landfill cell is planned to be built between points A and B as shown. The bottom of the landfill cell must be at least 5 feet above the water table at all points.
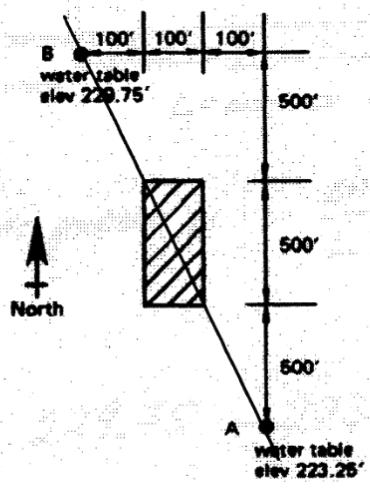
Determine:
- The hydraulic gradient between points A and B
- The minimum elevation of the waste cell.
- Estimate the travel time for contaminants to reach point A if the protective liner of the landfill cell fails and contaminated liquid seeps into the groundwater.
Solution
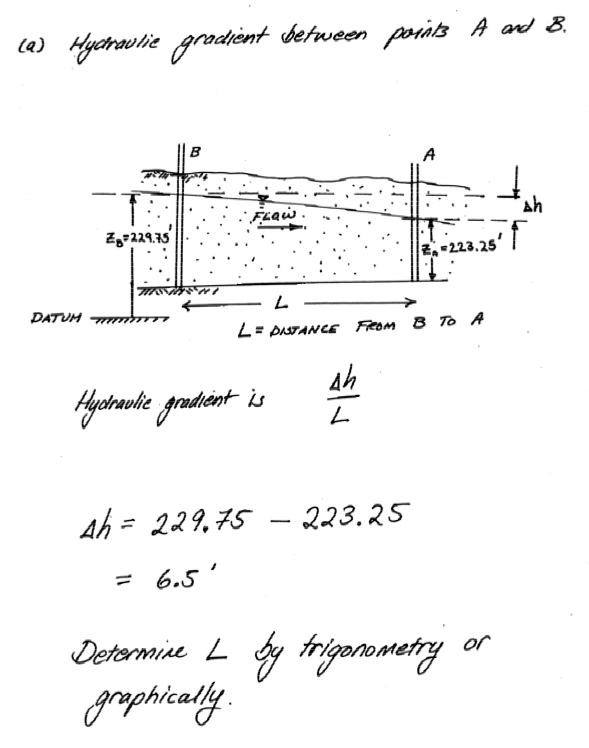
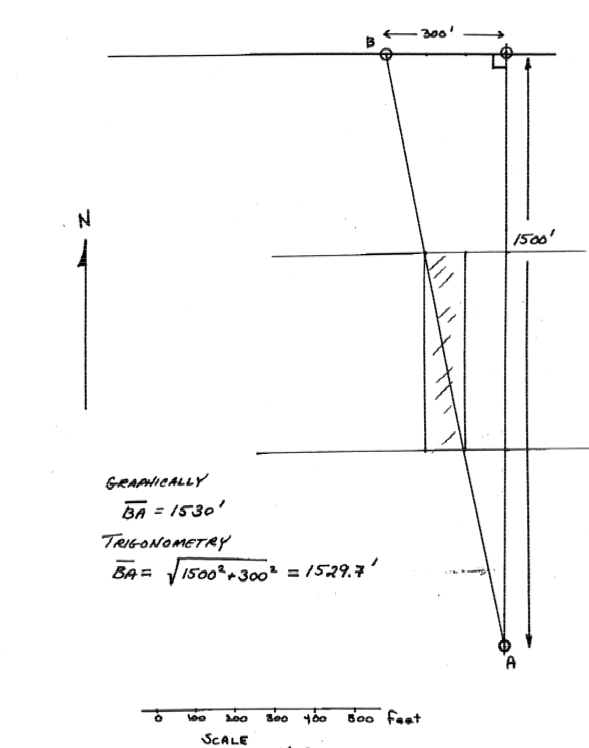
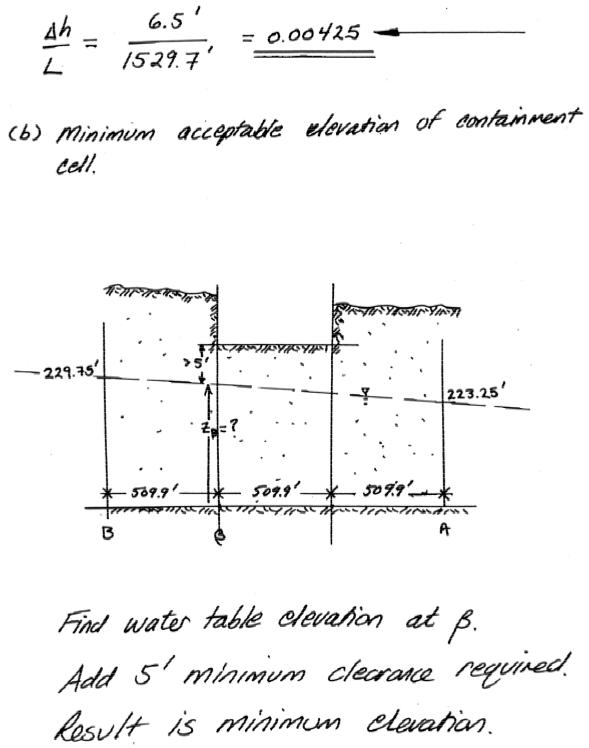

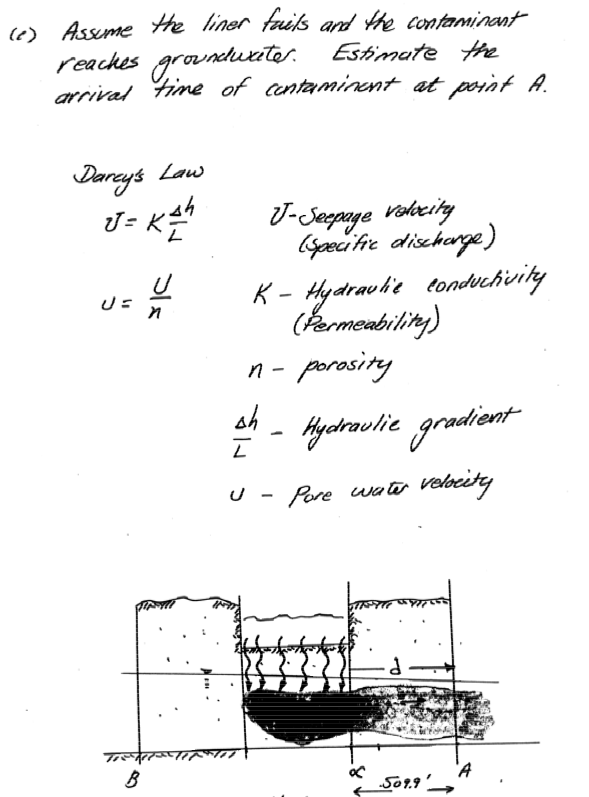


Question 10 (20 pts.)¶
The wells shown below are in a leaky confined aquifer. The aquifer has a hydraulic conductivity of 30 ft/d, saturated thickness of 45.0 ft, and storage coefficient of 0.00080. The aquitard above has a thickness of 8.0 ft and vertical conductivity of 0.45 ft/d. Well A was turned on at noon Sunday with a flow rate of 150 gpm. Well B was turned on at noon Tuesday with a flow rate of 200 gpm. Find the total drawdown in ft at the observation well C at noon Thursday.
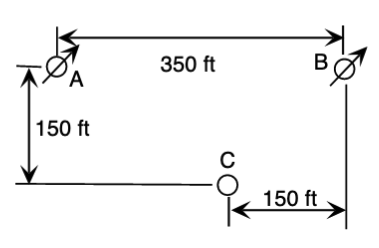
Solution
Apply image well theory and Hantush solution using supplied values
1) First copy-paste solution code from notes:
def wh(u, rho): # Hantush Leaky aquifer well function
import numpy
try:
u =float(u)
rho =float(rho)
except:
print("u and rho must be scalars.")
raise ValueError()
LOGINF = 2
y = numpy.logspace(numpy.log10(u), LOGINF, 1000)
ym = 0.5 * (y[:-1]+ y[1:])
dy = numpy.diff(y)
w = numpy.sum(numpy.exp(-ym - (rho / 2)**2 / ym ) * dy / ym)
return w
def W(u): # Theis well function using exponential integral
import scipy.special as sc
w = sc.expn(1,u)
return(w)
def s(radius,time,storage,transmissivity,discharge): # Drawdown function using exponential integral
import math
u = ((radius**2)*(storage))/(4*transmissivity*time)
s = ((discharge)/(4*math.pi*transmissivity))*W(u)
return(s)
def sleaky(radius,time,storage,transmissivity,discharge,leakance): # Drawdown function using exponential integral
import math
rho = radius/leakance
u = ((radius**2)*(storage))/(4*transmissivity*time)
s = ((discharge)/(4*math.pi*transmissivity))*wh(u,rho)
return(s)
2) Then set up simulation conditions
rAC = math.sqrt((350-150)**2+(150)**2) # distance well C to well A
rBC = math.sqrt((150)**2+(150)**2) # distance well C to well B
timeA = 4 # days, given 1200 Sunday to 1200 Thursday
timeB = 2 # days, given 1200 Tuesday to 1200 Thursday
QGPMA = 150 # given
QCFDA = QGPMA*(1/7.48)*(1440/1) # convert to ft^3/day
QGPMB = 200 # given
QCFDB = QGPMB*(1/7.48)*(1440/1) # convert to ft^3/day
T = 30*45 # ft^2/day - given
S = 0.00080 # given
bv = 8.0 # ft - given
kv = 0.45 # ft/day - given
B = math.sqrt((T*bv)/kv)
ddnCA = sleaky(rAC,timeA,S,T,QCFDA,B)
ddnCB = sleaky(rBC,timeB,S,T,QCFDB,B)
ddnC = ddnCA + ddnCB
print("Drawdown in Observation Well C :",round(ddnC,2)," feet")
Aside: a cooler version of the problem would be to produce a drawdown vs time plot at well C starting sunday at noon!
CE 5363 Question 11 (20 pts.)¶
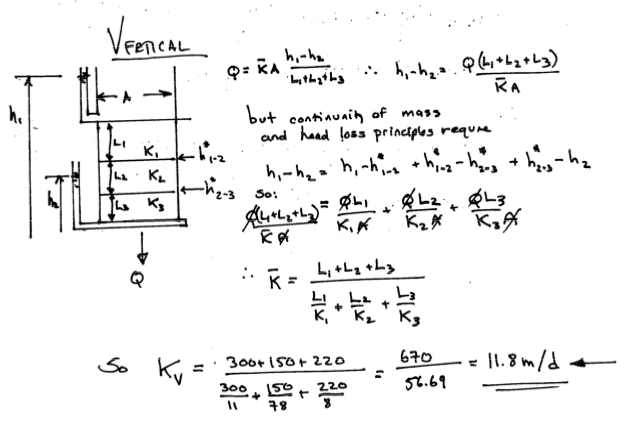
An aquifer is comprised of three formations as shown. Each individual formation is homogeneous and isotropic. Derive formulas for the overall apparent hydraulic conductivity in the horizontal and vertical directions, and apply the formulas to estimate the average horizontal and vertical hydraulic conductivtiy of the composite formation
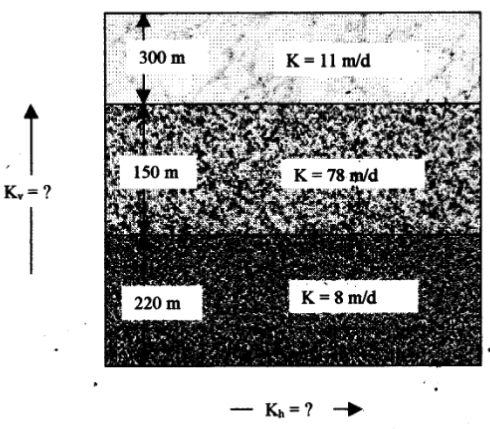
Solution
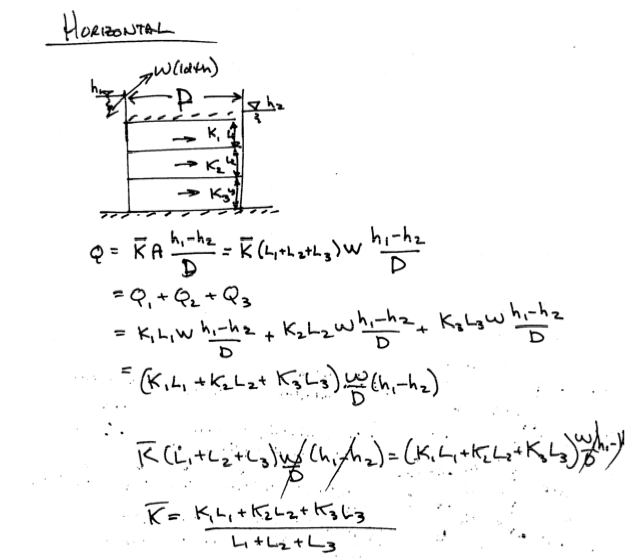
L1=300
L2=150
L3=220
K1=11
K2=78
K3=8
Kv = (L1+L2+L3)/((L1/K1)+(L2/K2)+(L3/K3))
Kh = ((K1*L1)+(K2*L2)+(K3*L3))/(L1+L2+L3)
print("Horizontal Average Hydraulic Conductivity :",round(Kh,3)," meters/day")
print("Vertical Average Hydraulic Conductivity :",round(Kv,3)," meters/day")
CE 5363 Question 12 (20 pts.)¶
A single pumping well exists in an ideal confined aquifer. The aquifer has a transmissivity of 4700 ft2/d and storage coefficient of 0.00025. The well is 85 ft west of a no-flow boundary that runs north-south. The pumping well has an effective radius of 0.50 ft, and pumps at a flow rate of 200 gpm.
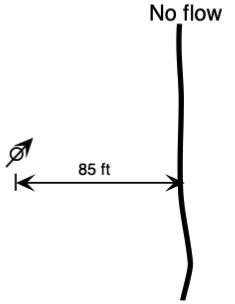
Determine:
- The total drawdown in ft at the pumping well at 6.0 hours after the well was turned on, ignoring characteristic well losses.
Solution
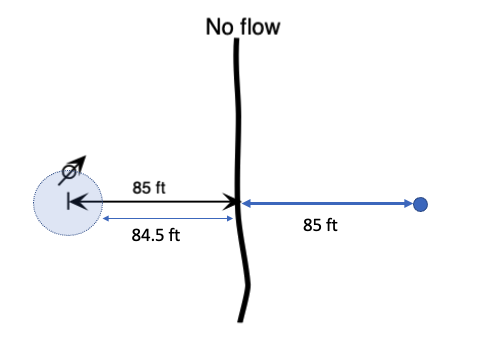
Apply method of images and Theis solution, notice here "effective radius" means the radius of the well.
def W(u): # Theis well function using exponential integral
import scipy.special as sc
w = sc.expn(1,u)
return(w)
def smodel(radius,time,storage,transmissivity,discharge): # Drawdown function using exponential integral
import math
u = ((radius**2)*(storage))/(4*transmissivity*time)
smodel = ((discharge)/(4*math.pi*transmissivity))*W(u)
return(smodel)
# distances relative to pumping well
r1 = 0.50 # ft radius of pumping well
r2 = 84.5 + 85 # ft distance to image well
T = 4700 # ft^2/day given
S = 0.00025 # given
QGPM = 200 # gpm given
QCFD = QGPM*(1/7.48)*(1440/1) # convert to ft^3/day
time = 6.0/24.0 # days given
ddn1=smodel(r1,time,S,T,QCFD)
ddn2=smodel(r2,time,S,T,QCFD)
ddn = ddn1+ddn2
print("Drawdown at pumping well screen redius :",round(ddn,3)," feets")
CE 5363 Question 13 (20 pts.)¶
The drawing below is a profile through an unconfined aquifer with two drains located left and right of the aquifer. Derive the equation that relates head in the aquifer to the recharge ($N$) and the position ($x$). The water level in the left drain is fixed at elevation $h_L = 10.0$ meters. The elevation of the land surface is $D=18.5$ meters. If the right drain is one kilometer from the left drain and the desired minimum depth to water is $d_{min} = 1.0$ meter, find the required elevation of water, $h_R$, in the right drain. The recharge rate is $N=0.001 \frac{m}{day}$, the hydraulic conductivity is $K=1.0 \frac{m}{day}$
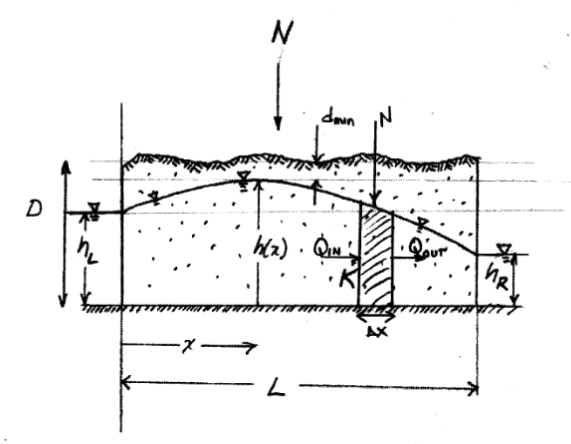
Solution
By hand analysis :
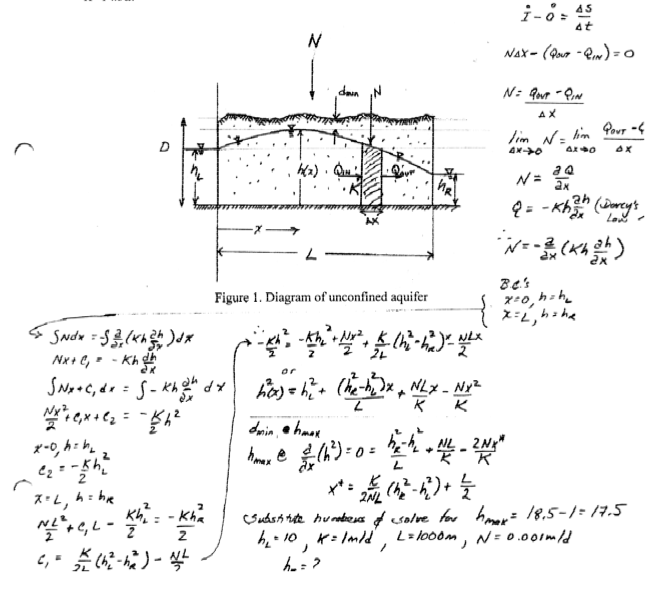

Or by computer plotting, goal is to find $h_R$ so that maximum head is 17.5 meters (1 meter below land surface)
# scripting
L = 1000 #m
K = 1.0 #m/d
N = 0.001 #m/d
hl = 10 #m given
hr = 2.89 #m guess and adjust
def ditch(x,hl,hr,L,N,K):
import math
ditch = math.sqrt(hl**2 + (((hr**2 - hl**2)*x)/(L)) + ((N*x)*(L-x)/(K)) )
return(ditch)
x=[0 for i in range(100)]
h=[0 for i in range(100)]
max = 0.0
for i in range(100):
x[i]=float(i)*10
h[i]=ditch(x[i],hl,hr,L,N,K)
if h[i]>max:
max=h[i]
from matplotlib import pyplot as plt
graph, (plt1) = plt.subplots(1, 1) # create a 1X1 plotting frame
plt1.plot(x, h, c='blue',linewidth=1) # basic line plot
#plt1.plot(x, h, c='red', marker='o',linewidth=0) # basic line plot
#plt1.set_xscale('log') # set x-axis to display a logarithmic scale #################
plt1.set_ylim([0,20])
plt1.set_xlabel('Time (ft)') # label the x-axis
plt1.set_ylabel('Drawdown (ft)') # label the y-axis, notice the LaTex markup
#plt1.legend(['Model','Observed']) # legend for each series
plt1.set_title('Head vs Distance Between 2 Ditches\n Left Ditch Head:' + str(round(hl,3)) + ' Right Ditch Head: ' + str(round(hr,3)) + "\nMax Head: " + str(round(max,3))) # make a plot title
plt1.grid() # display a grid
plt.show() # display the plot
CE 5363 Question 14 (20 pts.)¶
Calculate the porosity of uniform sized spheres packed in a body-centered cubic structure as shown below.

Solution
- First using Chat GPT 3.0 Completion Engine:
The porosity of a packing of uniform spheres in a body-centered cubic structure can be calculated as follows:
In a body-centered cubic structure, each sphere is in contact with six neighboring spheres. The spheres are arranged in such a way that there is a sphere at the center of the cube and another at each corner of the cube.
Let's consider a unit cell of the body-centered cubic structure, which contains two spheres. The diameter of each sphere is equal to the edge length of the cube. Therefore, the volume of each sphere is:
V_s = (4/3) pi (d/2)^3 = (4/3) pi (a/2)^3 (where d is the diameter of the sphere, and a is the edge length of the cube)
The volume of the unit cell is:
V_c = a^3
The total volume occupied by the spheres in the unit cell is:
V_p = 2 V_s = (8/3) pi * (a/2)^3
The porosity, P, is defined as the ratio of the void space (the space not occupied by the spheres) to the total volume:
P = (V_c - V_p) / V_c = (a^3 - (8/3) pi (a/2)^3) / a^3 = 1 - (8pi/3)(1/2)^3 = 1 - (2*pi/3) ≈ 0.259877
Therefore, the porosity of uniform sized spheres packed in a body-centered cubic structure is approximately 0.259877, or about 26%.
- Now the more conventional "human" approach
Here we see the computer answer and human answer differ! I would probably lean towards the human analysis, although the 6% difference is probably trivial
CE 5363 Question 15 (20 pts.)¶
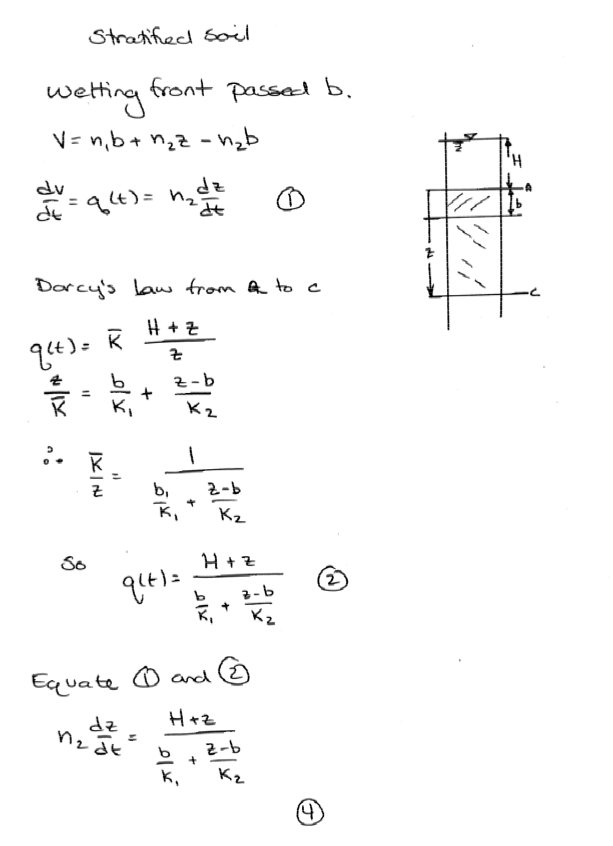
An artifical recharge pond is located in a sandy area (Kv = 10 m/day; porosity = 30%). The pond covers a large area. A flood wave fills the pond rapidly to a water level of 5.5 meters above the sandy bottom. By controlling the inflow and outflow the water level is maintained at this elevation. During previous operations, the bottom of the pond was covered by a layer of fine material 0.5 meters thick with Kv = 0.1 m/day and a porosity of 50%.
Assuming infiltration is vertically downward only, determine the position of the wetting front from the recharge pond into an initially dry soil as a function of time (derive an equation). Assume a very deep water table. What is the infiltration after a long time?
Solution
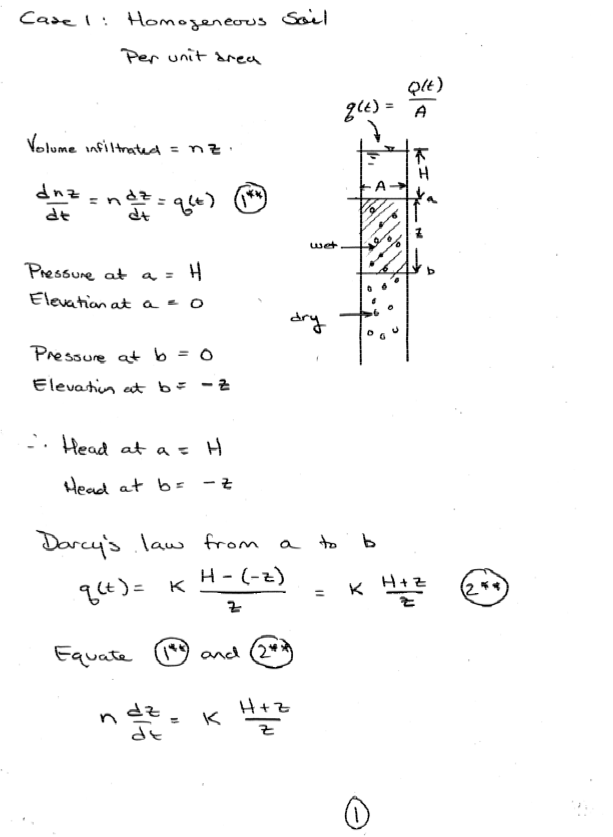
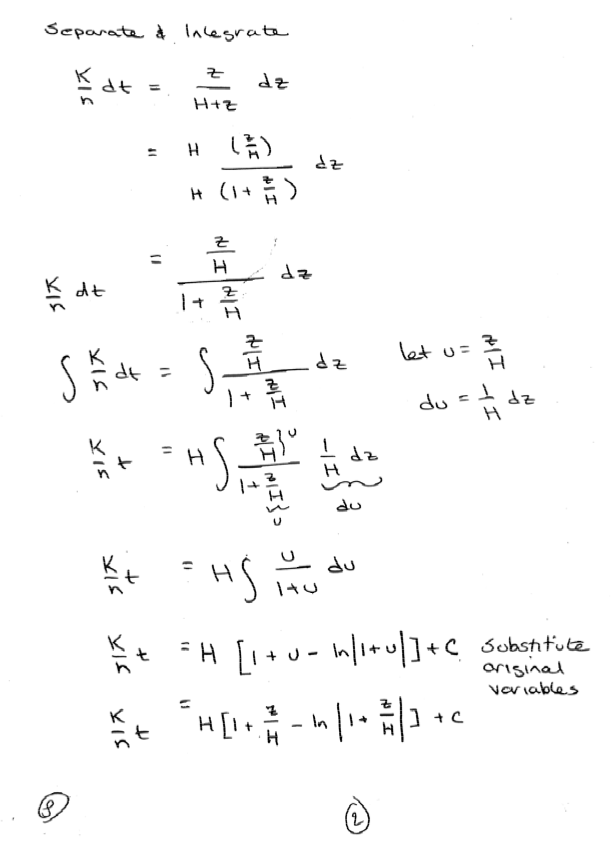

For a stratified soil extend the same concepts in Polubarinova-Kočina, P. Ya. (1952). Theory of motion of ground water. Moscow: Gosudarstv. Izdat. Tehn.-Teor. Lit. (English Translation) (actually a few pages later in the same document - sorry no copy herein)