Download (right-click, save target as ...) this page as a Jupyterlab notebook from: ES-7
CE 4353 Design of Hydraulic Systems
CE 5360 Open Channel Flow
Fall 2023 Exercise Set 7
LAST NAME, FIRST NAME
R00000000
Purpose :¶
Apply principles of uniform flow to open channel analysis and design
Assessment Criteria :¶
Completion, results plausible, format correct, calculations (Jupyter Notebook) are shown.
Instructions :¶
- CE 4353 Complete All Problems
- CE 5360 Complete All Problems
Problem 1¶
A trapezoidal roadside drainage ditch with a design discharge of 3.75 $\frac{m3}{s}$ is lined with grass having a retardance of class C. The slope of the ditch is 0.004 and it has a bottom width of 2.0 m with side slopes of 3:1.
Determine:
- Determine the design depth of flow
- Whether the channel is stable
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
Problem 2¶
Design a riprap-lined trapezoidal channel that has a capacity of 1000 cfs and a slope of 0.0005 ft/ft. Crushed rock is to be used and the channel bottom width is not to exceed 15 ft.
Determine:
- The riprap size.
- The side slopes.
- The design depth of flow.
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
Problem 3¶
A rectangular channel has a width of 10 ft and a Manning's n value of 0.020. Determine
Determine:
- The channel slope such that uniform flow will always have a Froude number less than or equal to 0.5 regardless of the discharge.
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
Problem 4¶
Figure 4 is a compound channel which has symmetric floodplains, each of which is 100 m wide with Manning's n = 0.06, and a main channel, which is trapezoidal with a bottom width of 10 m, side slopes of 1.5:1, a bank-full depth of 2.5 m, and a Manning’s n of 0.03. The channel longitudinal slope is 0.001 and the total depth is 3.7 m
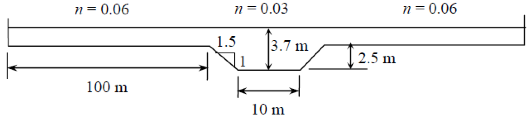
Determine:
- The uniform flow discharge using the divided channel method with vertical interfaces separating the main channel from the overbank areas and including these in the wetted perimeters
- The uniform flow discharge using the divided channel method with vertical interfaces separating the main channel from the overbank areas without including these in the wetted perimeters
- The uniform flow discharge using the divided channel method using the diagonal interface approach to separate the flow areas, but don’t use the diagonal interfaces in the wetted perimeters.
# sketch(s)
# list known quantities
# list unknown quantities
# governing principles
# solution details (e.g. step-by-step computations)
# discussion
