Download (right-click, save target as ...) this page as a Jupyterlab notebook from: ES-4

---

CE 4353/5360 Design of Hydraulic Systems
Fall 2022 Exercise Set 4

LAST NAME, FIRST NAME

R00000000

---

Purpose :

Apply principles of momentum conservation and rapidly varied flow concepts to open channel analysis and design

Assessment Criteria :

Completion, results plausible, format correct, calculations (Jupyter Notebook) are shown.

---

Problem 1

A hydraulic jump occurs in a 20 ft wide rectangular channel, the upstream depth is 3.5 ft at a flow rate of 2500 cfs.

Determine:

• The downstream depth in ft
• The head loss across the jump.

# sketch(s) here

# list known quantities

# list unknown quantities

governing principles

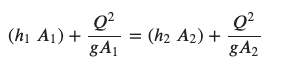
# solution (step-by-step/computations)
g = 32.2 # ft/s/s given
y1 = 3.5  # ft given
y2 = 14.99 #14.9936 # <<<< Guess this value, adjust to obtain momentum balance for section
Q  = 2500 # cfs given
b  = 20.0 # ft. given
deltaY = 0.0001
tolerance = 10000

def funcM(A,hc,Q,g):
    funcM = (A*hc)+(Q**2)/(g*A)
    return(funcM)

A1 = b*y1
A2 = b*y2
h1 = y1/2.0
h2 = y2/2.0
LHS = funcM(A1,h1,Q,g)
RHS = funcM(A2,h2,Q,g)
print("y1 = ",round(y1,3),"y2 = ",round(y2,4)," Momentum Error = ",round(LHS-RHS,3))

E1 = y1+Q**2/(2*g*A1**2)
E2 = y2+Q**2/(2*g*A2**2)
print("head loss ",round(E1-E2,3)," feet")

y1 =  3.5 y2 =  14.99  Momentum Error =  0.918
head loss  7.236  feet

---

Problem 2

A hydraulic jump is to be formed in a trapezoidal channel with a base width of 20 ft and side slopes of 2:1. The upstream depth is 1.35 ft and Q=1100 cfs. Figure 3-2 below is from the textbook.

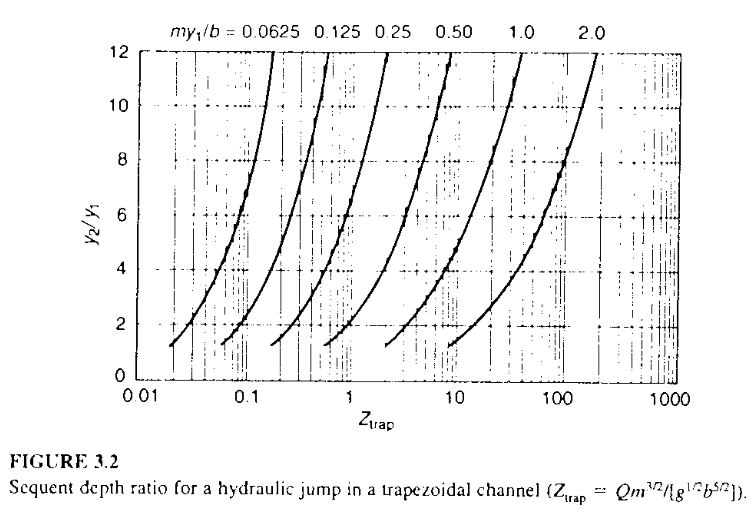
Determine:

• The downstream depth in the jump
• The head loss in the jump
• The approach momentum function value $M_1$
• The exit momentum function value $M_2$

# sketch(s) here

# list known quantities

# list unknown quantities

# governing principles

# solution (step-by-step/computations)
# just reuse code
g = 32.2 # ft/s/s given
y1 = 1.35  # ft given
y2 = 8.482 # <<<< Guess this value, adjust to obtain momentum balance for section
Q  = 1100 # cfs given
b  = 20.0 # ft. given
m  = 2.0 # given


def TopTrap(y,m,b):
    TopTrap=b+2*m*y
    return(TopTrap)
    
def AreaTrap(y,m,b):
    AreaTrap=y*(b+m*y)
    return(AreaTrap)

def funcM(A,hc,Q,g):
    funcM = (A*hc)+(Q**2)/(g*A)
    return(funcM)

def ybar(y,b,m):
    ybar=((m*y**3)/6+(b*y**2)/2+(m*y**3)/6)/(y*(b+m*y))
    return(ybar)

A1 = AreaTrap(y1,m,b)
A2 = AreaTrap(y2,m,b)
h1 = ybar(y1,b,m)
h2 = ybar(y2,b,m)
LHS = funcM(A1,h1,Q,g)
RHS = funcM(A2,h2,Q,g)
print("y1 = ",round(y1,3),"y2 = ",round(y2,4)," Momentum Error = ",round(LHS-RHS,3))

E1 = y1+Q**2/(2*g*A1**2)
E2 = y2+Q**2/(2*g*A2**2)
print("head loss ",round(E1-E2,3)," feet")

y1 =  1.35 y2 =  8.482  Momentum Error =  -0.029
head loss  12.684  feet

# discussion

---

Problem 3

A 3-ft diameter storm sewer carries a discharge of 6.5 cfs with a flow depth of 0.65 ft. Figure 3-3 below is from the textbook.

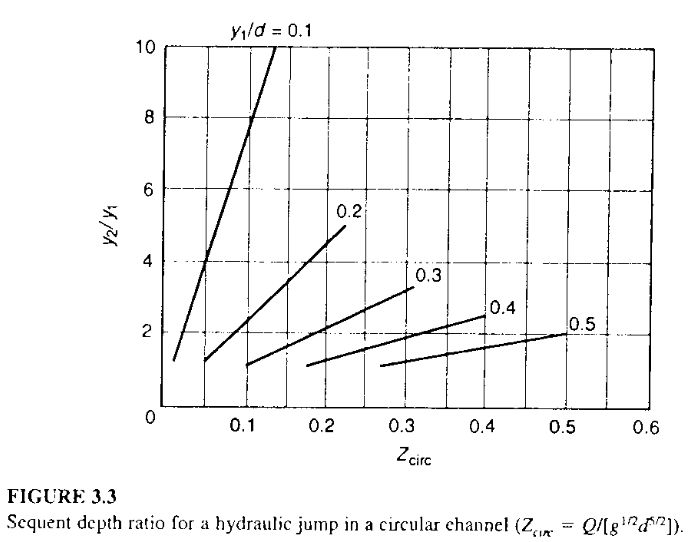
Determine:

• The downstream depth in the jump
• The head loss in the jump
• The approach momentum function value $M_1$
• The exit momentum function value $M_2$

# sketch(s) here

# list known quantities

# list unknown quantities

# governing principles

# solution (step-by-step/computations)
# just reuse code
g = 32.2 # ft/s/s given
y1 = 0.65  # ft given
y2 = 0.85 # <<<< Guess this value, adjust to obtain momentum balance for section
Q  = 6.5 # cfs given
diam  = 3.0 # ft. given
deltaY =0.0001
tolerance = 0.0001

#Angle = ARCCOS[1 - 2(y/D)] (in radians)
#Area = (D^2/4)(Angle - SIN(Angle)*COS(Angle))
#Topwidth = D*SIN(Angle)

def guppy(y,diam):
    import math
    guppy=math.acos(1.0-2*(y/diam))
    return(guppy)
    
def areaC(y,diam):
    import math
    areaC=((diam**2)/4)*(guppy(y,diam) - math.sin(guppy(y,diam))*math.cos(guppy(y,diam)))
    return(areaC)

def topC(y,diam):
    import math
    topC = diam*math.sin(guppy(y,diam))
    return(topC)
    

def funcM(A,hc,Q,g):
    funcM = (A*hc)+(Q**2)/(g*A)
    return(funcM)

def ybar(y,diam):
    import math
    ybar=(diam*math.sin(guppy(y,diam))/(3*guppy(y,diam)))
    return(ybar)
for i in range(1000):
    y2 += deltaY
    A1 = areaC(y1,diam)
    A2 = areaC(y2,diam)
    h1 = ybar(y1,diam)
    h2 = ybar(y2,diam)
    LHS = funcM(A1,h1,Q,g)
    RHS = funcM(A2,h2,Q,g)
    if abs(LHS-RHS) <= tolerance:
        print("y1 = ",round(y1,3),"y2 = ",round(y2,4)," Momentum Error = ",round(LHS-RHS,3))

y1 =  0.65 y2 =  0.8583  Momentum Error =  0.0
y1 =  0.65 y2 =  0.8584  Momentum Error =  0.0
y1 =  0.65 y2 =  0.8585  Momentum Error =  -0.0
y1 =  0.65 y2 =  0.8586  Momentum Error =  -0.0

y2=0.8585
A2 = areaC(y2,diam)
E1 = y1+Q**2/(2*g*A1**2)
E2 = y2+Q**2/(2*g*A2**2)
print("head loss ",round(E1-E2,3)," feet")

head loss  0.072  feet

discussion

A nice brute force approach; here's same solved by using charts first some dimensionless parameters

Zcirc = Q/math.sqrt(g*diam**5)
y1oD = y1/diam
print(Zcirc,y1oD)

Then use the chart

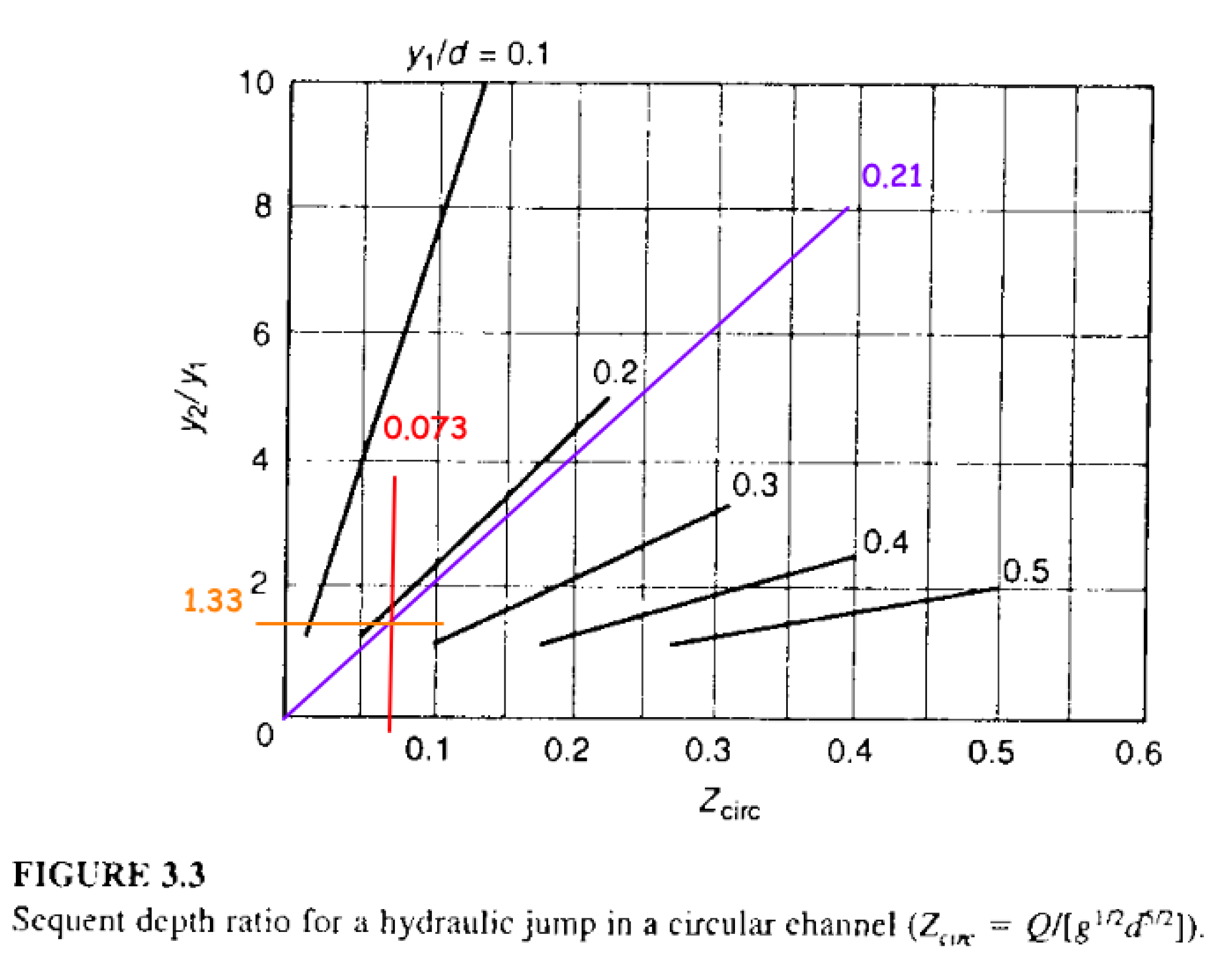
Then print the depth

print("y2 approx. ",1.33*y1)

y2 approx.  0.8645

Which is about the same as the momentum balance computations.

---

Problem 4

A flume with triangular cross section contains water flowing at a depth of 0.15 $m$ and at a discharge of 0.35 $\frac{m^3}{s}$. The side slopes of the flume are 2:1.

Determine:

• The downstream depth for a hydraulic jump
• The head loss in the jump
• The approach momentum function value $M_1$
• The exit momentum function value $M_2$

# sketch(s) here

# list known quantities

# list unknown quantities

# governing principles

# solution (step-by-step/computations)

# discussion