Download (right-click, save target as ...) this page as a Jupyterlab notebook from: ES-1

CE 4353/5360 Design of Hydraulic Systems
Fall 2022 Exercise Set 1

LAST NAME, FIRST NAME

R00000000

Purpose :

Assessment Criteria :

Completion, results plausible, format correct, calculations (Jupyter Notebook) are shown.

Problem 1

The river flow at an upstream gauging station is measured as 1500 $\frac{m^3}{sec}$, and at another gauging station 3 $km$ downstream, the discharge is measured as 750 $\frac{m^3}{sec}$ at the same moment in time. The channel is uniform, with a width of 300 $m$.

Determine:

  • The rate of change in the average water surface elevation in meters per hour.
  • Whether the stage (average water surface elevation) is rising or falling.
In [ ]:
# sketch(s) here
In [ ]:
# list known quantities
In [ ]:
# list unknown quantities
In [ ]:
# governing principles
In [ ]:
# solution (step-by-step/computations)
In [ ]:
# discussion

Problem 2

A paved parking lot section has a uniform slope over a length of 100 $m$ (in the flow direction) from the point of a drainage area divide to the inlet grate, which extends across the lot width of 30 $m$. Rainfall is occuring at a constant intensity of 100 $\frac{mm}{hr}$. The detention storage on the paved section is accumulating (increasing) at a rate of 60 $\frac{m^3}{hr}$

Determine:

  • Runoff rate into the inlet grate (in $\frac{m^3}{sec}$)
In [ ]:
# sketch(s) here
In [ ]:
# list known quantities
In [ ]:
# list unknown quantities
In [ ]:
# governing principles
In [ ]:
# solution (step-by-step/computations)
In [ ]:
# discussion

Problem 3

A symmetric compound channel in overbank flow has a main channel with a bottom width of 30 $m$, side slopes of 1:1,and a flow depth of 3 $m$. The floodplains on either side of the main channel are 300 $m$ wide and flowing at a depth of 0.5 $m$. The mean velocity in the main channel is 1.5 $\frac{m}{sec}$ whereas the floodplain flow portion has a mean section velocity of 0.3 $\frac{m}{sec}$. The velocity variation within the main channel and floodplain subsections are assumed to be much smaller than the change in mean velocities between subsections.

Determine:

  • The value of the kinetic energy correction coefficient $\alpha$
In [ ]:
# sketch(s) here
In [ ]:
# list known quantities
In [ ]:
# list unknown quantities
In [ ]:
# governing principles
In [ ]:
# solution (step-by-step/computations)
In [ ]:
# discussion

Problem 4

A bridge has cylindrical piers 1 $m$ in diameter and spaced 15 $m$ apart.
Downstream of the bridge, where the flow disturbance from the piers is no longer present, the flow depth is 2.9 $m$ and the mean velocity is 2.5 $\frac{m}{sec}$

Figure 4 is a typical graph of drag coefficient for a single cylinder

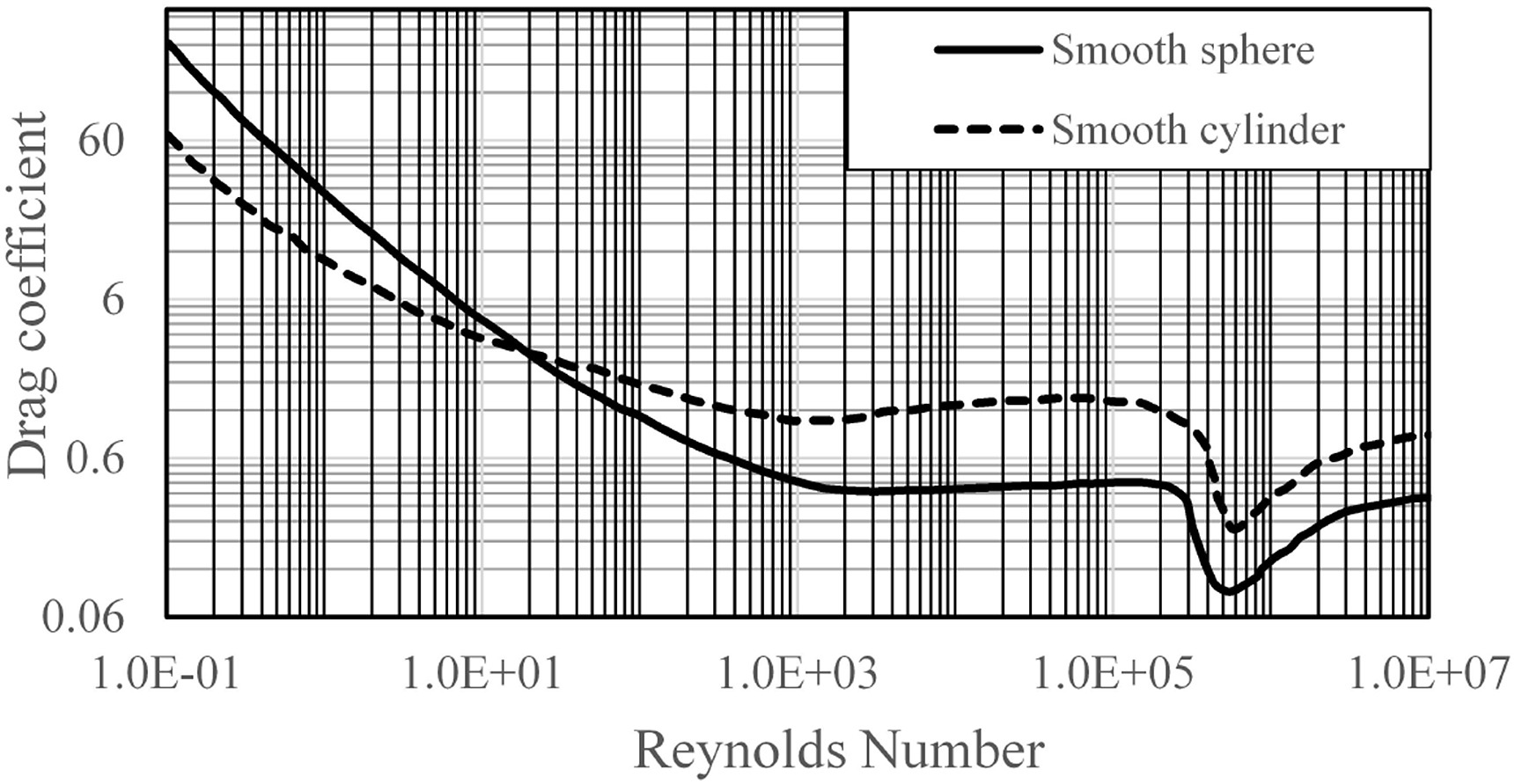
Figure 4 adapted from Wenjun Gao, Daniel Nelias, Yaguo Lyu, Nicolas Boisson, Numerical investigations on drag coefficient of circular cylinder with two free ends in roller bearings, Tribology International, Volume 123, 2018, Pages 43-49, ISSN 0301-679X, https://doi.org/10.1016/j.triboint.2018.02.044.

Figure 4: The drag coefficient, $C_D$, for a circular cylinder as a function of Reynolds number.

Determine

  • The Reynolds number for the flow described (use the flow depth as the characteristic length)
  • The drag coefficient, $C_d$ for a cylinder at the computed Reynolds number
  • The depth of flow upstream of the bridge
  • The head loss caused by the piers
In [ ]:
# sketch(s) here
In [ ]:
# list known quantities
In [ ]:
# list unknown quantities
In [ ]:
# governing principles
In [ ]:
# solution (step-by-step/computations)
In [ ]:
# discussion