Liquid Properties (pp. 46-52)¶
A liquid is one kind of fluid, but it has a few added properties that are important. One such property is surface tension, \(\sigma\).
Surface tension is the force per unit area required to separate two fluids. It is measured with a ring tensiometer https://en.wikipedia.org/wiki/Du_No%C3%BCy_ring_method, and a few other ways. Dimensionally it is a force per unit length, and is one reason why liquids can rise up capillary tubes, or into porous materials (like a sponge). Surface tension controls how liquids spread or bead up on a surface.
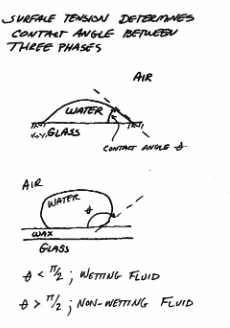
Wetting and non-wetting fluid-fluid-solid systems.¶
surface-tension is a schematic of a wetting and non-wetting drop of fluid onto a surface.
Capillary Rise¶
We can explain capillary rise using a force-balance and the concepts of wetting and non-wetting fluids.
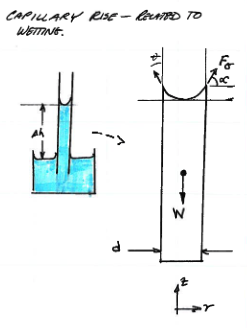
Schematic of capillary tube¶
capillary-fbd

Force balance analysis of portion above free surface.¶
capillary-analysis
Note
Some of the intermediate algebra is shown below to illustrate the terms that are cancelled. Many equations in the book are shown without intermediate steps; its up to you to trust explicitly, or check the intermediate steps yourselves - textbooks are a bit more reliable than Facebook for facts, but not much (even this notebook should be held suspect until you check the work for errors and ommissions!)
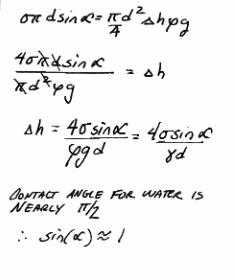
Intermediate algebra¶
capillary-algebra is some of the intermediate algebra for capillary tubes.
Using our equations and knowledge of contact angle for water in the note above we can calculate the rise in a capillary tube.
Example 3 - Capillary Tube¶
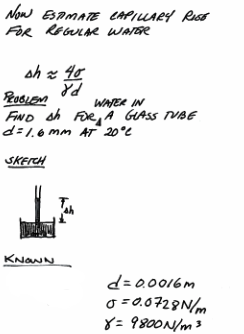
Intermediate algebra¶
capillary-water-1 is a brief problem statement, sketch, and list of known values.

Intermediate algebra¶
capillary-water-2 is the remainder of the solution, with a list of unknowns, the governing equation, and worked out solution. Notice the solution protocol is still followed but greatly simplified in this example.
