Intensive and Extensive Properties (pp. 28-35)¶
Extensive properties apply to a system and are associated with a fixed quantity of mass.
Intensive properties apply to components of a system, and are defined with restect to a boundary in space.
Imagine a gallon of water; its weight is an extensive property assocated with that gallon. The specific weight, \(\gamma\), is the weight per volume is an intensive property. The properties in the textboox (pp 14-19) are for the most part intensive properties (mostly defined per unit volume)
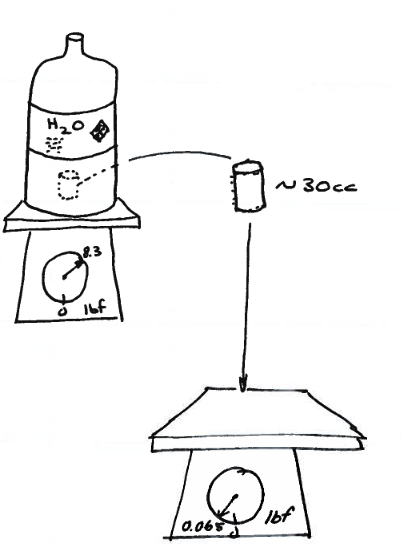
One gallon, and a 30cc sample removed¶
gallon-properties is a schematic of a simple example to relate extensive and intensive properties.
We first weigh the entire gallon, 8.32 lbs. Then we weigh the 30cc subsample, 0.065 lbs.
The extensive property of weight for the gallon is 8.32 lbs; the extensive property of weight for the 30cc is 0.065 lbs.
If we now compute specific weights of each entity and adjust to a common basis volume:
spwt_gallon = 8.32 # lbs per gallon
spwt_30cc = 0.065 # lbs per 30 cc
# convert to common volume
spwt_30cc = spwt_30cc*(128/1) # 30cc==1oz; 128oz==1gal conversion to common volume basis.
print('Sp. Wt. of 1 gallon sample = ',round(spwt_gallon,3))
print('Sp. Wt. of 30 cc sample = ',round(spwt_30cc,3))
Sp. Wt. of 1 gallon sample = 8.32
Sp. Wt. of 30 cc sample = 8.32
They are the same value (as anticipated); intensive properties are useful in most fluid mechanics problems because they are a property of a specific fluid, rather that some fixed volume of that fluid - however we must be comfortable using both.
Common Fluid Physical Properties¶
Density¶
Density (or mass density) is the mass per unit volume. Typical symbol is \(\rho\), sometimes subscripted to identify fluid in multiiple fluid problems.
Specific Weight¶
Specific weight is the weight per unit volume. Typical symbol is \(\gamma\). It is related to density by gravitational acceleration:
Specific Gravity¶
Specific gravity is the ratio of density of a fluid to a reference fluid. In Civil Engineering the reference fluid is typically liquid water. Typical symbol is \(S\)
Bulk Modulus (of elasticity)¶
The bulk modulus relates the change in volume of a fluid element to a change in pressure. For liquids it is quite high, gasses quite a bit smaller - it is essentially a Hooke’s law (springs) for a continuum element. It conveys how much pressure change is needed to effect a incremental volume change.
Dimensionally it is a pressure. For water at terresterial pressure and temperature its value is upwards of 2.2 GPa (about 23 atmospheres); for solid steel well over 150 GPa (about 1550 atmospheres).
In our practical sense, gas is compressible, water is not very compressible, steel smaller still.
All the properties above are temperature dependent, and in gasses the compressibility is small, hence they are called compressible fluids.
Common Thermodynamic Properties¶
A few thermodynamic properties are useful too:
Constant Volume Specific Heat¶
The heat amount added to a unit mass of fluid to raise the temperature one degree (units system dependent!) while volume is held constant.
Typical symbol is \(c_v\).
Constant Pressure Specific Heat¶
The heat amount added to a unit mass of fluid to raise the temperature one degree (units system dependent!) while pressure is held constant.
Typical symbol is \(c_p\).
Specific Internal Energy¶
Energy a unit mass possesses because of its state of molecular activity. Typical symbol is \(u\)
Note
The symbol \(u\) is also commonly used for the x-component, or streamline component of velocity. Be aware of context to avoid confusion. In some documents \(U\) is the velocity vector - again the context should be a clue.
Specific Enthalpy¶
Energy a substance possesses because of internal energy and applied normal stress (aka pressure). Typical symbol is \(h = u + \frac{p}{\rho}\)
Equation of State¶
The state of a fluid is the value of all its properties at specified temperature, pressure, and gravitational filed strength. The Ideal Gas Law is a relatively simple equation of state for gasses.

Ideal Gas Law (Equation of State)¶
pvnrt is the equation of state in two different forms for gasses. An equation of state allows prediction of state as temperature, pressure, or volume are changed.
