Download (right-click, save target as ...) this page as a Jupyterlab notebook from: ES-4

CE 3305 Engineering Fluid Mechanics
Summer 2022 Exercise Set 4

LAST NAME, FIRST NAME

R00000000

Purpose :

Apply concept of density and hydrostatic pressure in different fluids and determine pressure variation in layered fluids of different densities. Apply principles of manometry to determine density of unknown fluid.

Assessment Criteria :

Completion, plausible solutions, use of Jupyter Notebook as a calculator/documentation method

Problem 1.

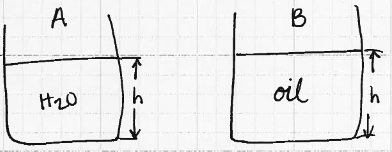
Imagine two tanks (both open to air). Tank A is filled to a depth $h$ with water. Tank B is filled to a depth $h$ with oil.

  • Which tank has the largest pressure?
  • Why?
  • Where in the tank does the largest pressure occur?

# sketch here

# list known quantities

  • depth of liquid ($h$)
  • type of liquid (water, oil)
  • implies that specific weight of the fluid(s) are known (Look up on the mighty internet!)

# list unknown quantities

# governing principles

AKA the hydrostatic equation

# solution (step-by-step)

# discussion

Direct application of hydrostatic equation for two different liquids.

Problem 2.

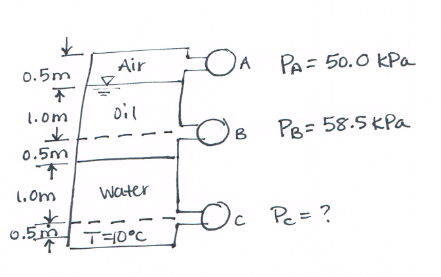
Figure 2 is a schematic of a closed tank with Bourdon-tube gages tapped into it.

  1. What is the specific gravity of the oil?
  2. What is the pressure reading on gage C?

# sketch here

# list known quantities

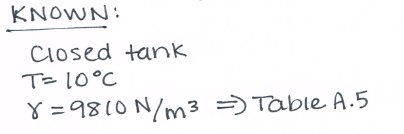
# list unknown quantities

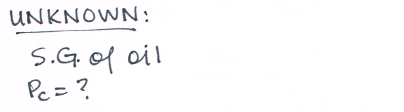
# governing principles

  • Hydrostatic equation ($p_2=p_1+\rho g h$)
  • Pascal's law

# solution (step-by-step)

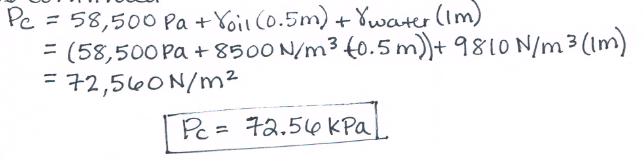
# discussion

Straighforward application of hydrostatic equation and Pascal's law.

Problem 3.

A device for measuring the specific weight of a liquid consists of a (U-,You-, or Ewe-) Tube manometer as depicted in Figure 3. The manometer tube has an internal diameter of $0.5~cm$ and originally has water in it. Exactly $2~cm^3$ of unknown liquid is poured into one leg of the manometer, and a displacement of $5~cm$ is measured between the free surfaces as shown.

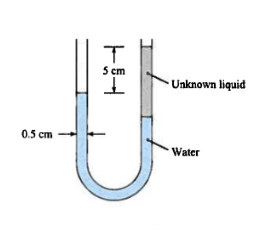
What is the specific weight of the unknown liquid?

# sketch here

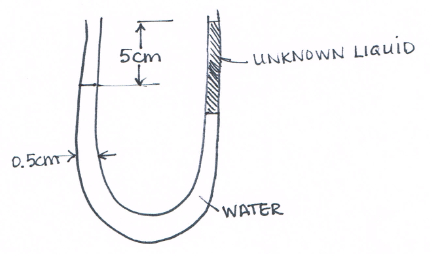
# list known quantities

# list unknown quantities

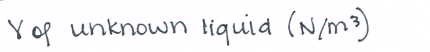
# governing principles

# solution (step-by-step)

A script to generalize for other cases

In [4]:
import math
diameter = 0.5 #cm
length = 2*4/(math.pi*diameter**2)
print("Length = ",round(length,3)," centimeters")
gamma_l = (5.186*0.01*9810)/(10.186*0.01)
print("sp. weight (unknown liquid) = ",round(gamma_l,3)," N/m^3 ")

Length =  10.186  centimeters
sp. weight (unknown liquid) =  4994.567  N/m^3

# discussion

Direct application of manometer equation (Pascal's law)

In [ ]: