Download (right-click, save target as ...) this page as a Jupyterlab notebook from: ES-13
Problem 1.¶
Figure 1 is a schematic of a hydropower system. The elevation difference between the reservoir water surface and the pond water surface downstream of the reservoir (called the tailwater), H, is 24 m. The velocity of the water exiting into the pond is 7 m/s, and the discharge through the system is 4 $m^3/s$.
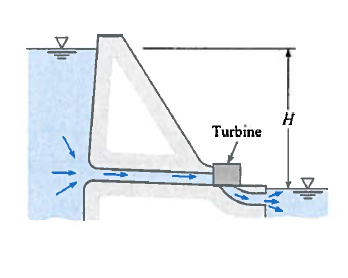
Neglecting frictional losses in the penstock (the pipe from the reservoir to the turbine) determine:
- The power produced by the turbine in kilowatts.
sketch here
list known quantities
list unknown quantities
governing principles
solution (step-by-step)
# code cell(s) here
discussion
Problem 2.¶
Figure 1 depicts a reservoir draining through a valve used to control the flow rate. The head loss across the valve is $h_l = \frac{4V^2}{2g}$ , where V is the velocity in the pipe. The cross-sectional area of the pipe is 8 $cm^2$.
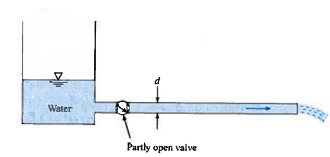
The elevation of the water level in the reservoir above the pipe outlet is 9 m.
Determine:
- The discharge in the pipe assuming all loss occurs in the valve (e.g. pipe loss is small compared to valve loss).; assume $\alpha = 1.0$ at all locations in the system.
sketch here
list known quantities
list unknown quantities
governing principles
solution (step-by-step)
# code cell(s) here
discussion
Problem 3¶
The figure below schematic of a pump system that supplies water to a hydraulic component through a 15 cm diameter, 60 m length of pipe. The mean velocity in the pipe is 2 m/s, and the head loss in the pipe is 2 m.
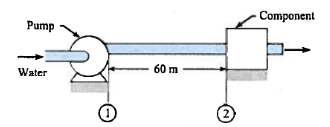
Determine:
- The pressure drop in the horizontal pipe
- The power required from the pump to overcome the head loss in the pipe.
sketch here
list known quantities
list unknown quantities
governing principles
solution (step-by-step)
# code cell(s) here
discussion