Problem 1. (Problem 8-19 pg.441)¶
The discharge, $Q$, over the weir $A$ depends on the width, $b$, of the weir, the head, $H$ above the weir crest, and the gravitational acceleration constant, $g$.
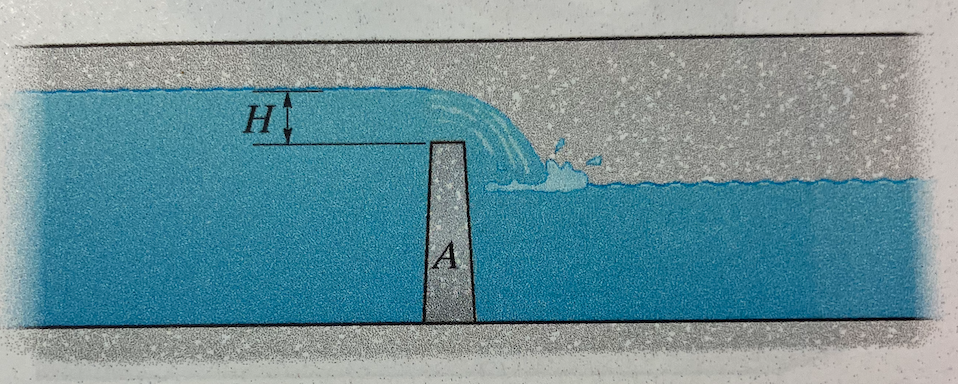
For the case(s) where $Q$ is known to be directly proportional to $b$,
Determine:
- The relation between $Q$ and these parameters.
- The resulting value for $Q$ if $H$ is doubled.
sketch here
list known quantities
list unknown quantities
governing principles
solution (step-by-step)
# code cell(s) here
discussion
Problem 2. (Problem 8-53 pg. 446)¶
The flow of water around a bridge pier is to be studied with a $\frac{1}{15}$ scale model.
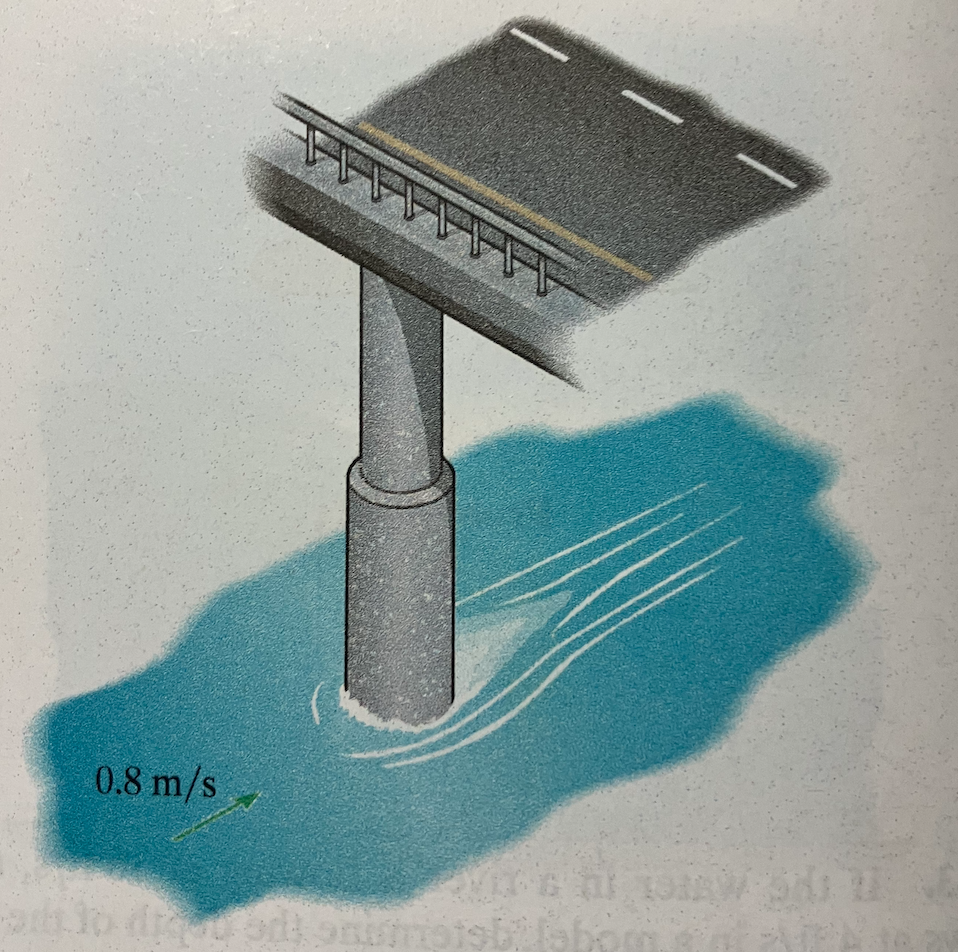
The anticipated river (prototype) velocity is 0.8 m/s.
Determine:
- The water velocity in the model at the same temperature.
sketch here
list known quantities
list unknown quantities
governing principles
solution (step-by-step)
# code cell(s) here
discussion
Problem 3.¶
A smooth pipe prototype designed to carry crude oil:
- $D = 47$ inches
- $\rho= 1.75$ slugs/$ft^3$
- $\mu= 4 \times 10^{−4}~ lbf − s/ft^2$
is to be modeled with a smooth pipe 4 inches in diameter carrying water (T =60$^o$F ). If the mean velocity in the prototype is to be 2 ft/s, what should be the mean velocity of the water in the model to ensure dynamically similar conditions?
sketch here
list known quantities
list unknown quantities
governing principles
solution (step-by-step)
# code cell(s) here
discussion